一、
R编辑器下载地址:https://cran.r-project.org/mirrors.html
安装教程:
R自学(各个包的详细描述):https://mirrors.tuna.tsinghua.edu.cn/CRAN/
二、R语言数据的存储结构
1.向量
#向量的两种表示方法
xiangliang1=c(1,2,3,4)#默认是列向量(用行显示是为了方便),c是连接函数
xiangliang1 #结果:[1] 1 2 3 4
xiangliang2=5:8#返回的是5到8的一个整型向量
xiangliang2 #结果:[1] 5 6 7 8
#索引
xiangliang1[2] #取出第二个向量 结果:2
xiangliang1[c(2,3)]#取出第二三个向量 结果:2,3
#xiangliang1[2,3] 错误,只能用上述方法
#注:向量和标量做运算(加减乘除)时,要把标量循环补齐
xiangliang2>5#结果:[1] FALSE TRUE TRUE TRUE 注:逻辑向量
xiangliang2[xiangliang2>5]#结果:[1] 6 7 8 注:逻辑值为True就取出相应位置的元素
xiangliang2+5#结果:[1] 10 11 12 13
xiangliang2[2:4]#结果: [1] 6 7 8 取出第二到四的元素
xiangliang2[c(2,3,4)]#上式的另一种方法
#seq(a,b,(length=5))生成一个最小值为a,最大值为b,长度为n的等差数列。注意该数列是向量(seq函数输出格式为向量)
dengcha1=seq(1,10,length=5)#生成一个1到10的等差数列,长度为5
dengcha1 #结果:[1] 1.00 3.25 5.50 7.75 10.00
dengcha2=seq(12,20,by=2)#步长为2
dengcha2
#查看函数用法(弹出解释界面)
?seq
?c
2.矩阵
x=matrix(1:9,3,3)#按照列的顺序,生成3*3的矩阵 x
结果是:
[,1] [,2] [,3] [1,] 1 4 7 [2,] 2 5 8 [3,] 3 6 9
y=matrix(1:9,3,3,byrow=T)#按照行的顺序,生成3*3的矩阵 y
结果是:
[,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9
x=matrix(1:9,3,3)#按照列的顺序,生成3*3的矩阵 x y=matrix(1:9,3,3,byrow=T)#按照行的顺序,生成3*3的矩阵 y x[,1]#取出矩阵第一列 [1] 1 2 3 x[1,]#取出矩阵第一行 [1] 1 4 7 x[1:2,]#取出矩阵第一二行 # [,1] [,2] [,3] #[1,] 1 4 7 #[2,] 2 5 8 x[3,2]#取出矩阵第三行第二列元素 [1] 6
3.数据框:形式上和矩阵是一样的
data.frame(3:5,6:8)
结果是:
X3.5 X6.8 1 3 6 2 4 7 3 5 8
x=data.frame(a=2:11,b=3:12)#每行叫做一个样本(观测),每列叫做变量 x
结果是:
a b
1 2 3
2 3 4
3 4 5
4 5 6
5 6 7
6 7 8
7 8 9
8 9 10
9 10 11
10 11 12
x[9,]#取出数据框第九行 # a b #9 10 11 x[,1]#取出数据框的第一列 [1] 2 3 4 5 6 7 8 9 10 11 x$a#上式的另一种方法 [1] 2 3 4 5 6 7 8 9 10 11
cars#速度与刹车距离组成的数据框(50个样本)
speed dist
1 4 2
2 4 10
3 7 4
4 7 22
5 8 16
6 9 10
7 10 18
8 10 26
9 10 34
10 11 17
11 11 28
12 12 14
13 12 20
14 12 24
15 12 28
16 13 26
17 13 34
18 13 34
19 13 46
20 14 26
21 14 36
22 14 60
23 14 80
24 15 20
25 15 26
26 15 54
27 16 32
28 16 40
29 17 32
30 17 40
31 17 50
32 18 42
33 18 56
34 18 76
35 18 84
36 19 36
37 19 46
38 19 68
39 20 32
40 20 48
41 20 52
42 20 56
43 20 64
44 22 66
45 23 54
46 24 70
47 24 92
48 24 93
49 24 120
50 25 85
iris#鸢尾花组成的数据框(150个样本)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa 7 4.6 3.4 1.4 0.3 setosa 8 5.0 3.4 1.5 0.2 setosa 9 4.4 2.9 1.4 0.2 setosa 10 4.9 3.1 1.5 0.1 setosa 11 5.4 3.7 1.5 0.2 setosa 12 4.8 3.4 1.6 0.2 setosa 13 4.8 3.0 1.4 0.1 setosa 14 4.3 3.0 1.1 0.1 setosa 15 5.8 4.0 1.2 0.2 setosa 16 5.7 4.4 1.5 0.4 setosa 17 5.4 3.9 1.3 0.4 setosa 18 5.1 3.5 1.4 0.3 setosa 19 5.7 3.8 1.7 0.3 setosa 20 5.1 3.8 1.5 0.3 setosa 21 5.4 3.4 1.7 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 23 4.6 3.6 1.0 0.2 setosa 24 5.1 3.3 1.7 0.5 setosa 25 4.8 3.4 1.9 0.2 setosa 26 5.0 3.0 1.6 0.2 setosa 27 5.0 3.4 1.6 0.4 setosa 28 5.2 3.5 1.5 0.2 setosa 29 5.2 3.4 1.4 0.2 setosa 30 4.7 3.2 1.6 0.2 setosa 31 4.8 3.1 1.6 0.2 setosa 32 5.4 3.4 1.5 0.4 setosa 33 5.2 4.1 1.5 0.1 setosa 34 5.5 4.2 1.4 0.2 setosa 35 4.9 3.1 1.5 0.2 setosa 36 5.0 3.2 1.2 0.2 setosa 37 5.5 3.5 1.3 0.2 setosa 38 4.9 3.6 1.4 0.1 setosa 39 4.4 3.0 1.3 0.2 setosa 40 5.1 3.4 1.5 0.2 setosa 41 5.0 3.5 1.3 0.3 setosa 42 4.5 2.3 1.3 0.3 setosa 43 4.4 3.2 1.3 0.2 setosa 44 5.0 3.5 1.6 0.6 setosa 45 5.1 3.8 1.9 0.4 setosa 46 4.8 3.0 1.4 0.3 setosa 47 5.1 3.8 1.6 0.2 setosa 48 4.6 3.2 1.4 0.2 setosa 49 5.3 3.7 1.5 0.2 setosa 50 5.0 3.3 1.4 0.2 setosa 51 7.0 3.2 4.7 1.4 versicolor 52 6.4 3.2 4.5 1.5 versicolor 53 6.9 3.1 4.9 1.5 versicolor 54 5.5 2.3 4.0 1.3 versicolor 55 6.5 2.8 4.6 1.5 versicolor 56 5.7 2.8 4.5 1.3 versicolor 57 6.3 3.3 4.7 1.6 versicolor 58 4.9 2.4 3.3 1.0 versicolor 59 6.6 2.9 4.6 1.3 versicolor 60 5.2 2.7 3.9 1.4 versicolor 61 5.0 2.0 3.5 1.0 versicolor 62 5.9 3.0 4.2 1.5 versicolor 63 6.0 2.2 4.0 1.0 versicolor 64 6.1 2.9 4.7 1.4 versicolor 65 5.6 2.9 3.6 1.3 versicolor 66 6.7 3.1 4.4 1.4 versicolor 67 5.6 3.0 4.5 1.5 versicolor 68 5.8 2.7 4.1 1.0 versicolor 69 6.2 2.2 4.5 1.5 versicolor 70 5.6 2.5 3.9 1.1 versicolor 71 5.9 3.2 4.8 1.8 versicolor 72 6.1 2.8 4.0 1.3 versicolor 73 6.3 2.5 4.9 1.5 versicolor 74 6.1 2.8 4.7 1.2 versicolor 75 6.4 2.9 4.3 1.3 versicolor 76 6.6 3.0 4.4 1.4 versicolor 77 6.8 2.8 4.8 1.4 versicolor 78 6.7 3.0 5.0 1.7 versicolor 79 6.0 2.9 4.5 1.5 versicolor 80 5.7 2.6 3.5 1.0 versicolor 81 5.5 2.4 3.8 1.1 versicolor 82 5.5 2.4 3.7 1.0 versicolor 83 5.8 2.7 3.9 1.2 versicolor 84 6.0 2.7 5.1 1.6 versicolor 85 5.4 3.0 4.5 1.5 versicolor 86 6.0 3.4 4.5 1.6 versicolor 87 6.7 3.1 4.7 1.5 versicolor 88 6.3 2.3 4.4 1.3 versicolor 89 5.6 3.0 4.1 1.3 versicolor 90 5.5 2.5 4.0 1.3 versicolor 91 5.5 2.6 4.4 1.2 versicolor 92 6.1 3.0 4.6 1.4 versicolor 93 5.8 2.6 4.0 1.2 versicolor 94 5.0 2.3 3.3 1.0 versicolor 95 5.6 2.7 4.2 1.3 versicolor 96 5.7 3.0 4.2 1.2 versicolor 97 5.7 2.9 4.2 1.3 versicolor 98 6.2 2.9 4.3 1.3 versicolor 99 5.1 2.5 3.0 1.1 versicolor 100 5.7 2.8 4.1 1.3 versicolor 101 6.3 3.3 6.0 2.5 virginica 102 5.8 2.7 5.1 1.9 virginica 103 7.1 3.0 5.9 2.1 virginica 104 6.3 2.9 5.6 1.8 virginica 105 6.5 3.0 5.8 2.2 virginica 106 7.6 3.0 6.6 2.1 virginica 107 4.9 2.5 4.5 1.7 virginica 108 7.3 2.9 6.3 1.8 virginica 109 6.7 2.5 5.8 1.8 virginica 110 7.2 3.6 6.1 2.5 virginica 111 6.5 3.2 5.1 2.0 virginica 112 6.4 2.7 5.3 1.9 virginica 113 6.8 3.0 5.5 2.1 virginica 114 5.7 2.5 5.0 2.0 virginica 115 5.8 2.8 5.1 2.4 virginica 116 6.4 3.2 5.3 2.3 virginica 117 6.5 3.0 5.5 1.8 virginica 118 7.7 3.8 6.7 2.2 virginica 119 7.7 2.6 6.9 2.3 virginica 120 6.0 2.2 5.0 1.5 virginica 121 6.9 3.2 5.7 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 123 7.7 2.8 6.7 2.0 virginica 124 6.3 2.7 4.9 1.8 virginica 125 6.7 3.3 5.7 2.1 virginica 126 7.2 3.2 6.0 1.8 virginica 127 6.2 2.8 4.8 1.8 virginica 128 6.1 3.0 4.9 1.8 virginica 129 6.4 2.8 5.6 2.1 virginica 130 7.2 3.0 5.8 1.6 virginica 131 7.4 2.8 6.1 1.9 virginica 132 7.9 3.8 6.4 2.0 virginica 133 6.4 2.8 5.6 2.2 virginica 134 6.3 2.8 5.1 1.5 virginica 135 6.1 2.6 5.6 1.4 virginica 136 7.7 3.0 6.1 2.3 virginica 137 6.3 3.4 5.6 2.4 virginica 138 6.4 3.1 5.5 1.8 virginica 139 6.0 3.0 4.8 1.8 virginica 140 6.9 3.1 5.4 2.1 virginica 141 6.7 3.1 5.6 2.4 virginica 142 6.9 3.1 5.1 2.3 virginica 143 5.8 2.7 5.1 1.9 virginica 144 6.8 3.2 5.9 2.3 virginica 145 6.7 3.3 5.7 2.5 virginica 146 6.7 3.0 5.2 2.3 virginica 147 6.3 2.5 5.0 1.9 virginica 148 6.5 3.0 5.2 2.0 virginica 149 6.2 3.4 5.4 2.3 virginica 150 5.9 3.0 5.1 1.8 virginica
4.列表:主要来存储一些函数的输出
x=list(a=6:9,b=10:13,c=c("天津","商业"))
x
结果是:
$a [1] 6 7 8 9 $b [1] 10 11 12 13 $c [1] "天津" "商业"
x$a#取出第一个变量(属于向量) [1] 6 7 8 9 x[[1]]#和上式效果一样,用两个中括号说明返回值的类型和a的类型是一样的,所以不能x[1]这样用 x$b[2]#取出b元素(向量)中的第二个元素 [1] 11
三、
1. if语句
#例1
x=66
if(x>=60){y=1
}else{y=0} #}esle必须和上边换行且放在一行
y #[1] 1
#例2
if(x>=60){z=10}
z #[1] 10
#例3
x=90
if(x>=60){if(x>=70){if(x>=80){if(x>=90){y=4
}else{y=3}
}else{y=2}
}else{y=1}
}else{y=0}
y #[1] 4
2. for循环
x=numeric(100)#生成100维的零向量
x
#结果:
#[1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# [37] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# [73] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#i表示的是位置,for循环是知道循环的圈数的
for(i in 1:100){
x[i]=2
}
x
#结果:
# [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# [37] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# [73] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
3. while循环
#while循环不知道循环的圈数的
x=numeric(100)
i=1#i称为循环控制变量
while(i<=50){
x[i]=2
i=i+1#i+=1不适合R
}
x
#结果:
# [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# [37] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# [73] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
四、文件的读取
数据中每一行叫做一个观测或者一个样本,每一列叫做一个变量
编译器改变默认路径方法:点击文件选项------》改变工作目录
1.读文件
c=read.csv("d:/111.csv",header=T)#header=T表示将表头读进去,同时把表头作为变量的名字
c
t=read.table("d:/111.txt",header=T)
t
#注意:用的是双引号和反斜杠/,也可以用两个正斜杠\\,如"d:\\111.csv"
结果:
学号 成绩
1 1 58
2 2 59
3 3 60
4 4 61
5 5 62
6 6 63
7 7 64
8 8 65
9 9 66
10 10 67
2.写文件
c=read.csv("d:/111.csv",header=T)
write.table(c,"d:/333.text")
五、自定义函数以及函数的编写
#输入x,y,输出(x+y),给函数起一个名字f
f=function(x,y){
return(x+y)
}
f(2,3)#[1] 5
sin(0)
#R中函数三个要素:输入,输出,函数名
介绍一些重要函数:https://www.cnblogs.com/xihehe/p/7473981.html (一定要看)
cars apply(cars,2,mean)#按列求均值 注:apply函数用于矩阵的运算
结果:
> cars speed dist 1 4 2 2 4 10 3 7 4 4 7 22 5 8 16 6 9 10 7 10 18 8 10 26 9 10 34 10 11 17 11 11 28 12 12 14 13 12 20 14 12 24 15 12 28 16 13 26 17 13 34 18 13 34 19 13 46 20 14 26 21 14 36 22 14 60 23 14 80 24 15 20 25 15 26 26 15 54 27 16 32 28 16 40 29 17 32 30 17 40 31 17 50 32 18 42 33 18 56 34 18 76 35 18 84 36 19 36 37 19 46 38 19 68 39 20 32 40 20 48 41 20 52 42 20 56 43 20 64 44 22 66 45 23 54 46 24 70 47 24 92 48 24 93 49 24 120 50 25 85 > apply(cars,2,mean)#按列求均值 speed dist 15.40 42.98
小知识:R中主要函数来进行统计计算,很多函数放在包里面的,而包是需要安装的。包安装完之后,必须加载,然后可以使用其中的函数。安装包之前需要提前设置镜像为中国的,步骤:点击编译器中的程序包选项,设定CRAN镜像,选择中国的;然后在编辑器中输入 install.packages("包的名字"),再输入 library(包的名字)进行加载包
install.packages("quantreg")
library(quantreg)
R 一般把数据放到内存中再来处理,但是缺点就是内存如果只有1G大小,R只能最多处理1G大小的数据
library(MASS)#MASS是自带的包 #quine#5个自变量,146个样本的数据 #?quine#查看该数据的用处 quine[,5]#引用第五列 quine$Days#引用第五列 attach(quine)#attach函数把数据框quine放到内存 #当把数据框放进内存中,可以简便的引用 Days#引用第五列,不用像上述两种引用第五列方法那样麻烦
library(MASS)#MASS是自带的包 str(quine)#str函数用来查看数据类型
结果:
'data.frame': 146 obs. of 5 variables: $ Eth : Factor w/ 2 levels "A","N": 1 1 1 1 1 1 1 1 1 1 ... $ Sex : Factor w/ 2 levels "F","M": 2 2 2 2 2 2 2 2 2 2 ... $ Age : Factor w/ 4 levels "F0","F1","F2",..: 1 1 1 1 1 1 1 1 2 2 ... $ Lrn : Factor w/ 2 levels "AL","SL": 2 2 2 1 1 1 1 1 2 2 ... $ Days: int 2 11 14 5 5 13 20 22 6 6 ...
data.frame:数据框 obs:观测 variables:变量
Factor指的是分类变量类型。也叫因子类型
2 levels "A","N":两类,分为A种族和N种族
library(MASS) attach(quine) #计算女生,男生旷课的天数 tapply(Days,Sex,mean) #tapply分类汇总函数 #结果 # F M #15.22500 17.95455
str(tapply(Days,Sex,mean))#查看类型 #tapply返回值类型为向量 # num [1:2(1d)] 15.2 18 #二维向量 # - attr(*, "dimnames")=List of 1 # ..$ : chr [1:2] "F" "M"
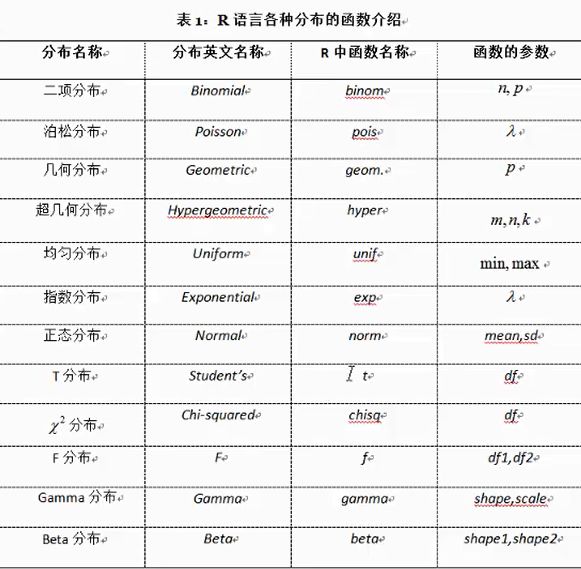
R中关于随机数的生成的函数:均匀分布,指数分布,正太分布
r+分布的名字:该分布的随机数
d+分布的名字:该分布的密度函数值
p+分布的名字:该分布的分布函数值
q+分布的名字:该分布的分位点的值
示例如下:
#生成10个来自N(0,4)的随机数 rnorm(10,0,2)#标准差是2 方差是4 #结果: # [1] -1.2890521 -0.2594150 -0.2050323 -0.8702874 -4.5483221 -0.7911182 # [7] 3.8099254 1.5759880 -0.4671626 0.7049596 #生成5个均匀分布的随机数 runif(5,1,3) #[1] 1.328076 1.384769 2.338306 1.210036 2.088914 runif(5,1,3)#和上个不同 #[1] 2.457805 1.105783 1.488697 1.458045 1.453241 #如果希望随机数固定,应当设置种子 set.seed(1) runif(5,1,3)#每次运行的结果相同 #正态分布在x=10这个点的密度函数值 dnorm(10,0,2)#[1] 7.433598e-07 #正态分布的95%的分位点 qnorm(0.95,0,2)#[1] 3.289707
六、画图,R的画图功能是非常强大的
散点图和线图:
描点法画图:把所有的横坐标放在第一个参数,把所有的纵坐标放在第二个参数
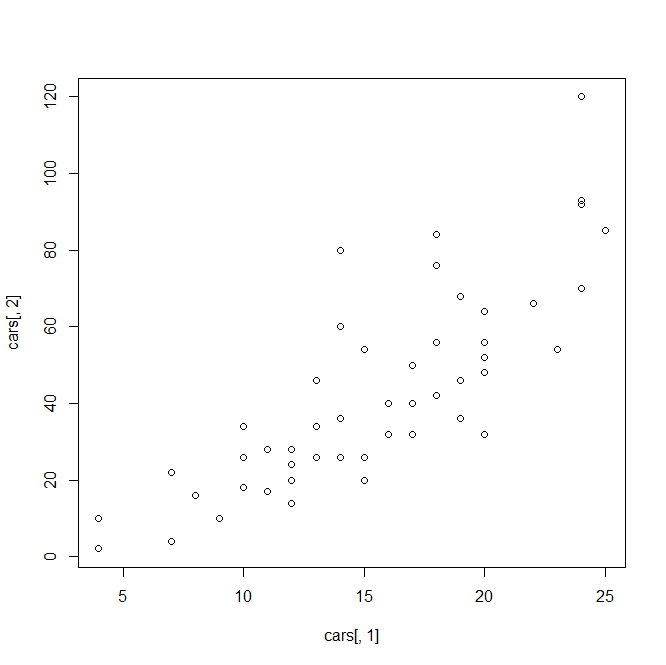
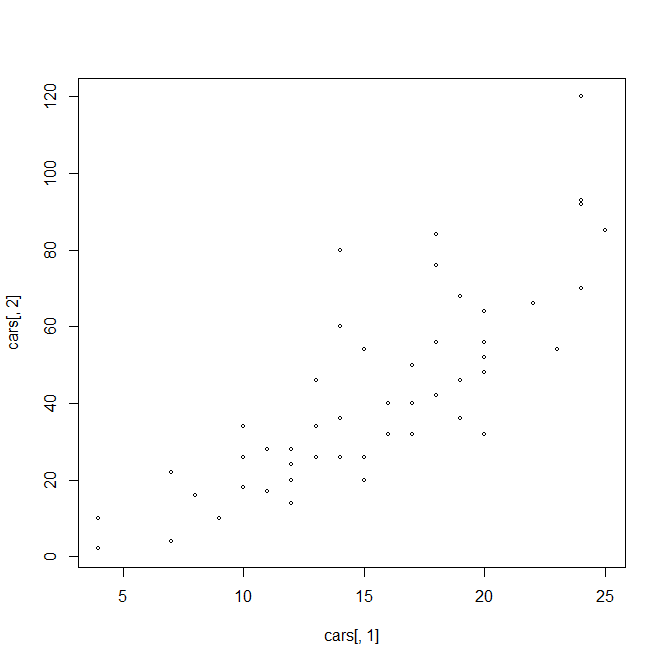
#cars 50个样本,2个变量 plot(cars[,1],cars[,2])
结果:
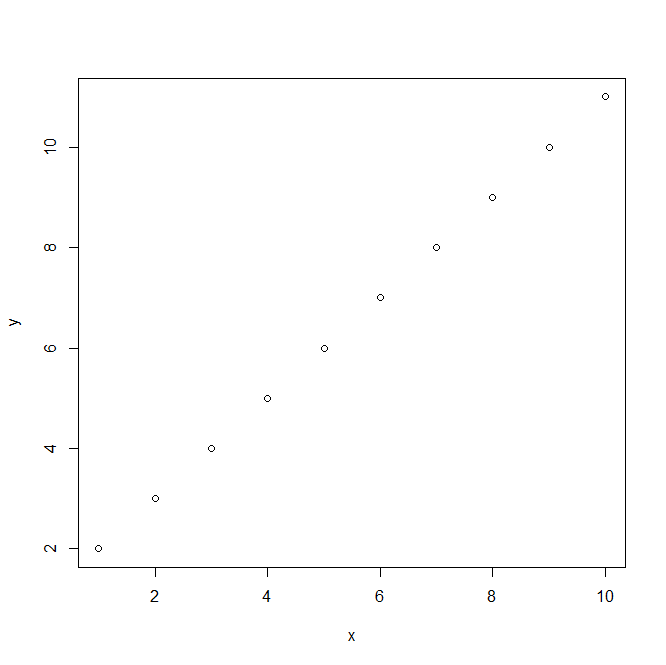
x=1:10 y=2:11 plot(x,y)#散点图
结果:
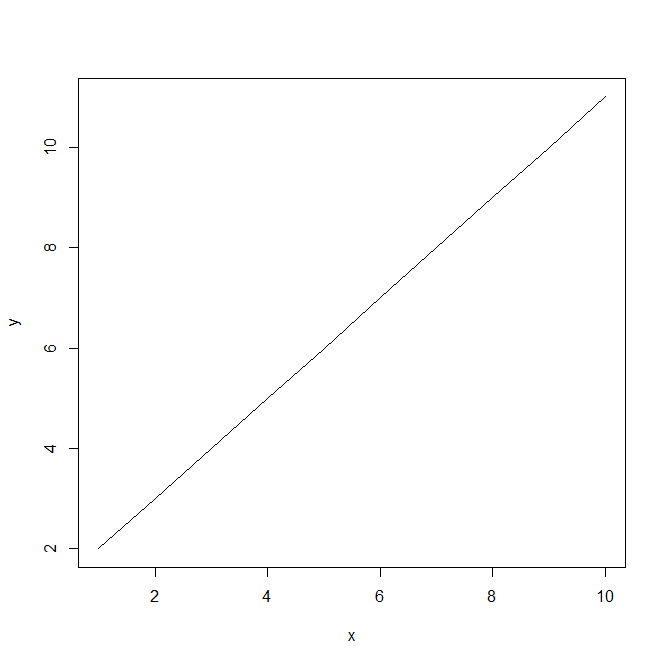
plot(x,y,type="l")#线性图(折线图)
结果:
plot(x,y,type="b")#既有直线又有点,但线不穿过点
结果:
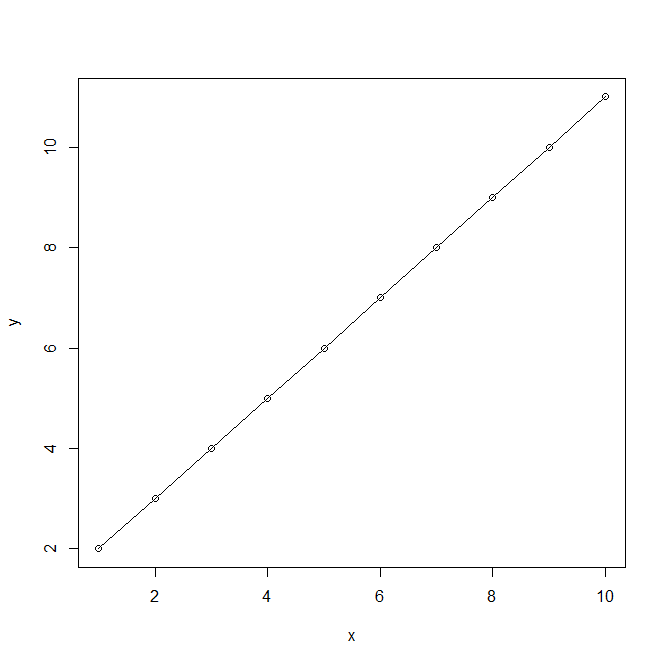
plot(x,y,type="o")#既有直线又有点,线穿过点
结果:
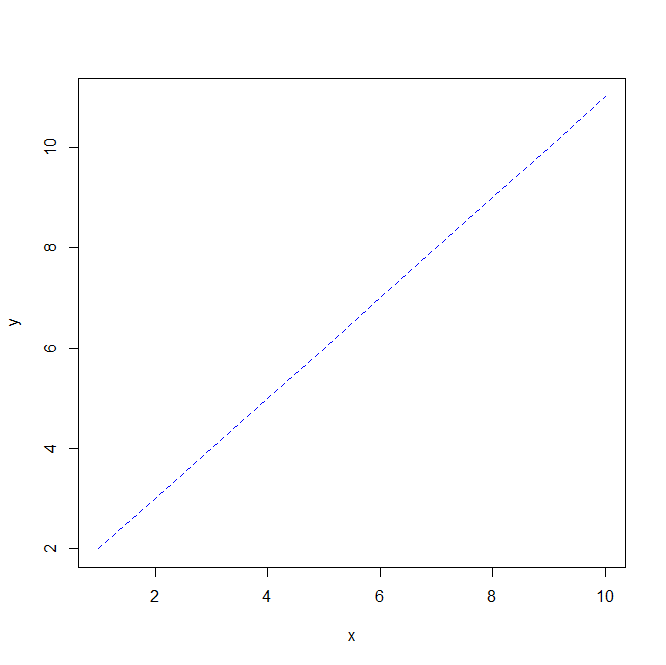
plot(x,y,type="l",col="blue",lty=2)#lty默认为1是实线,2为虚线,col代表颜色 ?plot#查看plot函数的用法,以及参数设置
结果:
plot是高级绘图函数,会自动生成一个图像界面。低级绘图函数,不会自动生成一个图像界面,只可以在高级绘图函数基础之上添加图像
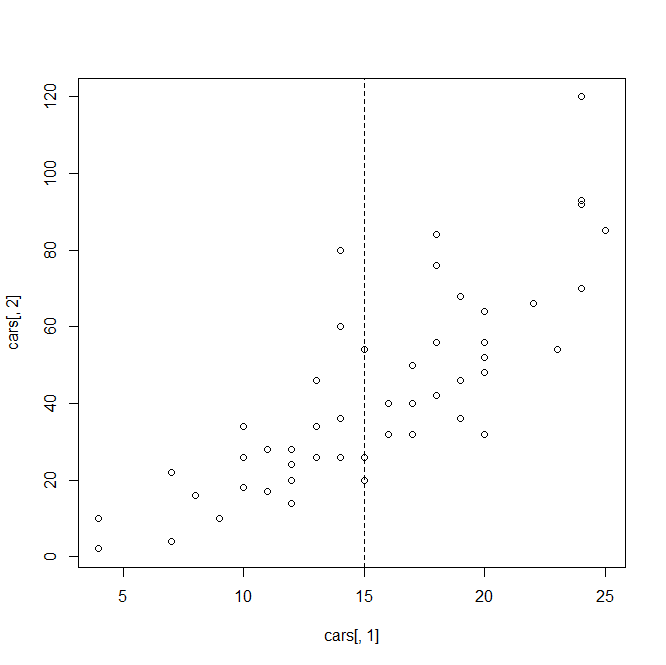
plot(cars[,1],cars[,2])#高级绘图函数 abline(v=15,lty=2)#在x=15处画一条竖直的虚线 低级绘图函数
结果:
plot(cars[,1],cars[,2],cex=0.5)#cex=1为默认状态,代表了点的大小
结果:
直方图:
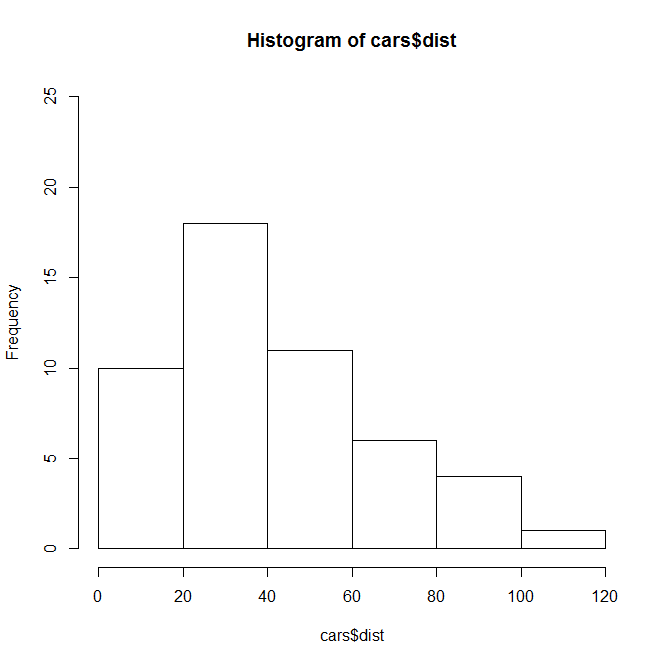
cars #hist画直方图,属于高级绘图函数 hist(cars$dist,ylim=c(0,25))#ylim设置的是纵坐标的图像显示范围,可以不写 频数直方图
结果:
speed dist
1 4 2
2 4 10
3 7 4
4 7 22
5 8 16
6 9 10
7 10 18
8 10 26
9 10 34
10 11 17
11 11 28
12 12 14
13 12 20
14 12 24
15 12 28
16 13 26
17 13 34
18 13 34
19 13 46
20 14 26
21 14 36
22 14 60
23 14 80
24 15 20
25 15 26
26 15 54
27 16 32
28 16 40
29 17 32
30 17 40
31 17 50
32 18 42
33 18 56
34 18 76
35 18 84
36 19 36
37 19 46
38 19 68
39 20 32
40 20 48
41 20 52
42 20 56
43 20 64
44 22 66
45 23 54
46 24 70
47 24 92
48 24 93
49 24 120
50 25 85
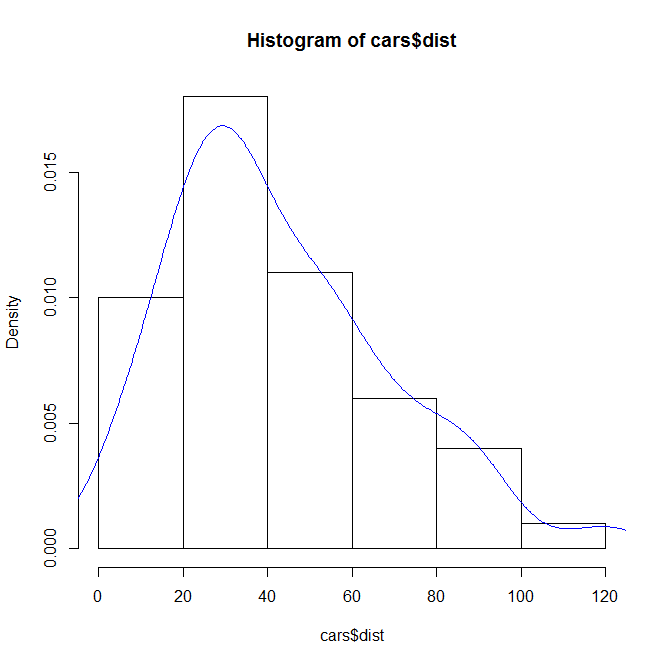
hist(cars$dist,freq=F)#频率直方图 lines(density(cars$dist),col="blue")#lines低级绘图函数 density核密度估计
结果:
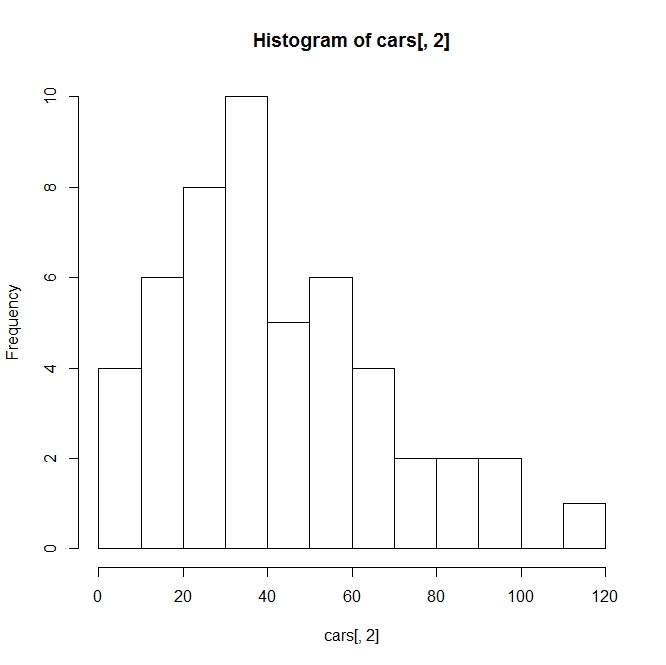
hist(cars[,2],breaks=10)#组距,直方图的柱子的数量
结果:
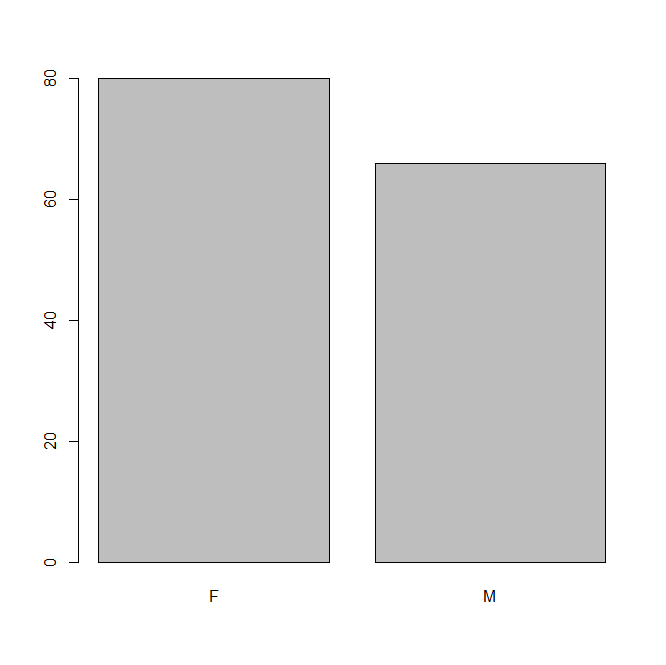
柱状图:barplot
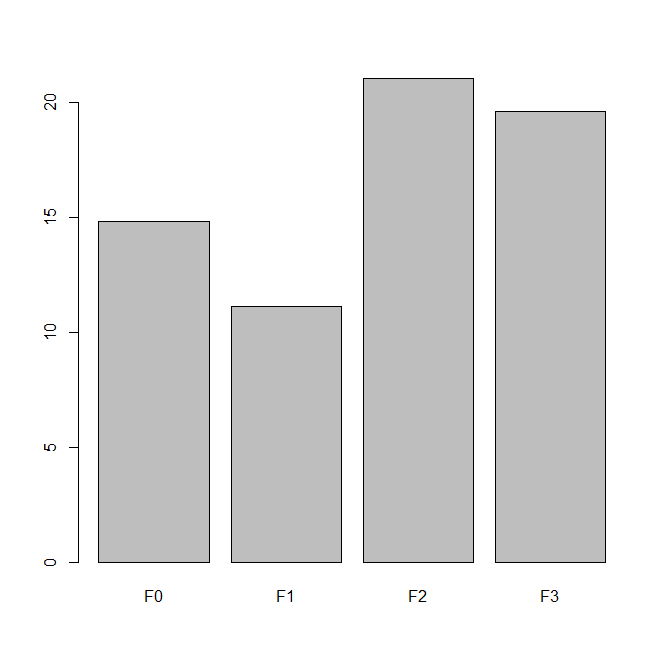
library(MASS) attach(quine) table(Sex)#统计分类变量,各类的频数 本处统计的是男女性别个数 #结果: Sex # F M # 80 66 barplot(table(Sex)) a=tapply(Days,Age,mean)#统计各年龄段的平均旷课天数 a #结果: F0 F1 F2 F3 # 14.85185 11.15217 21.05000 19.60606 barplot(a) b=tapply(Days,list(Sex,Age),mean)#统计两种性别各年龄段的平均旷课天数 b #结果: F0 F1 F2 F3 # F 18.70000 12.96875 18.42105 14.00000 # M 12.58824 7.00000 23.42857 27.21429 barplot(b)
结果:
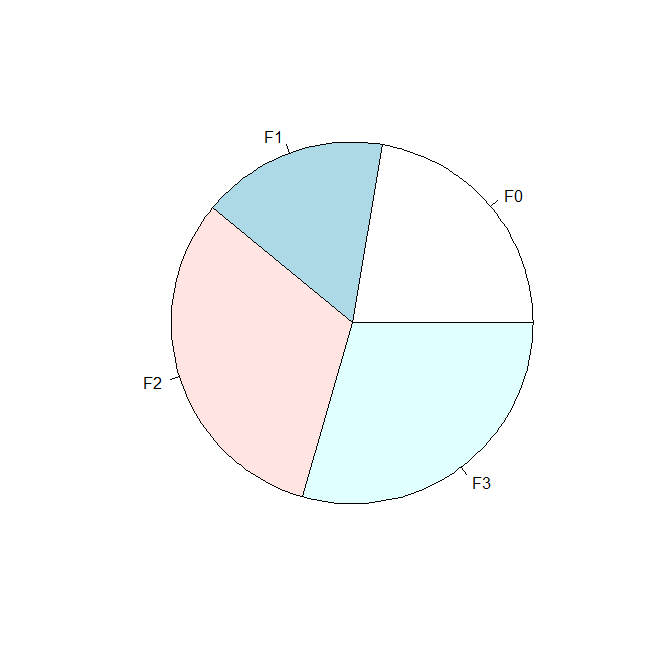
饼状图:pie 用来表示每部分占比
a=tapply(Days,Age,mean)#统计各年龄段的平均旷课天数 pie(a)
结果:
茎叶图:stem 用的不多
将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少。
stem(cars[,2])
结果:
The decimal point is 1 digit(s) to the right of the | 0 | 24004678 2 | 002466668822244466 4 | 002668024466 6 | 046806 8 | 04523 10 | 12 | 0
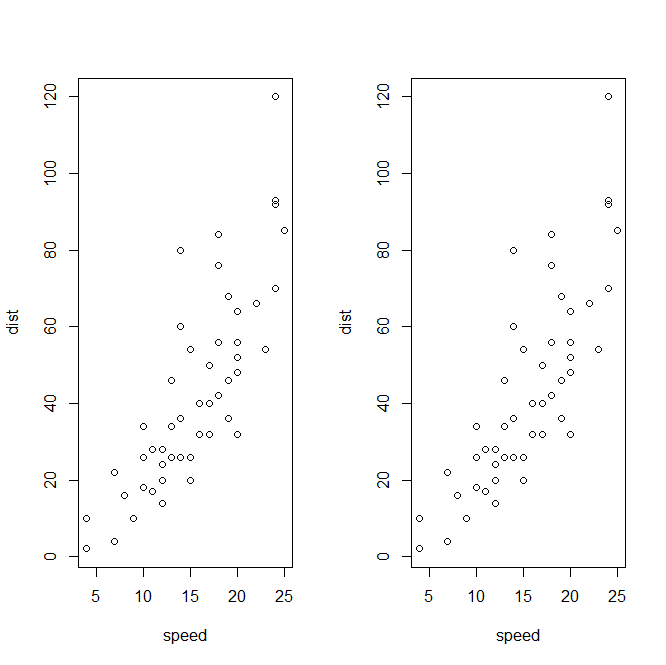
#par图形设备函数 par(mfrow=c(2,1))#画两行一列的图,可更改行列数 按行排序 plot(cars) plot(cars)
结果:
par(mfcol=c(1,2))#画两行一列的图,可更改行列数 按行排序 plot(cars) plot(cars)
结果:
七、
1.假设检验和区间估计
shapiro.test:检验样本是否服从正态分布
原假设是目标样本服从正态分布,用样本计算出来的p值>0.05,那么就不能拒绝原假设,目标样本服从正态分布
set.seed(12) a=rnorm(100,0,1) #检验a是否服从正态分布 shapiro.test(a)
结果:
Shapiro-Wilk normality test
data: a
W = 0.98945, p-value = 0.6201
ks.test:检验目标样本是否服从指定的连续型分布
原假设:检验目标服从指定的连续型分布,用样本计算出来的p值>0.05,那么就接收原假设,否则拒绝
set.seed(12) a=rnorm(100,0,1) #检验a是否服从N(2,2)的正态分布 分布前边加p(p+分布的名字:该分布的分布函数值) ks.test(a,"pnorm",2,2)
结果:
One-sample Kolmogorov-Smirnov test data: a D = 0.60747, p-value < 2.2e-16 alternative hypothesis: two-sided
chisq.test:检验目标样本是否服从指定的离散型分布,用法同上
t.test:假设检验(t检验),区间估计
t检验原假设:检验正态总体的均值为0( t检验在总体方差未知、样本方差已知的情况使用,总体方差已知用z检验); t.test函数还可以对总体的均值做区间估计,条件是总体方差未知( t检验在总体方差未知、样本方差已知的情况使用,总体方差已知用z检验)
set.seed(12) a=rnorm(100,0,1) #t检验 t.test(a) #p值>0.05,接收原假设,a来自的这个总体的均值为0 #95 percent confidence interval:95%的置信区间(注:总体均值的置信区间) ?t.test#置信度通过conf.level修改
结果:
One Sample t-test data: a t = -0.36029, df = 99, p-value = 0.7194 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: -0.2028249 0.1404875 sample estimates: mean of x -0.03116866
2.回归,逐步回归和回归分析诊断
回归:lm函数 回归的统计量:summary函数
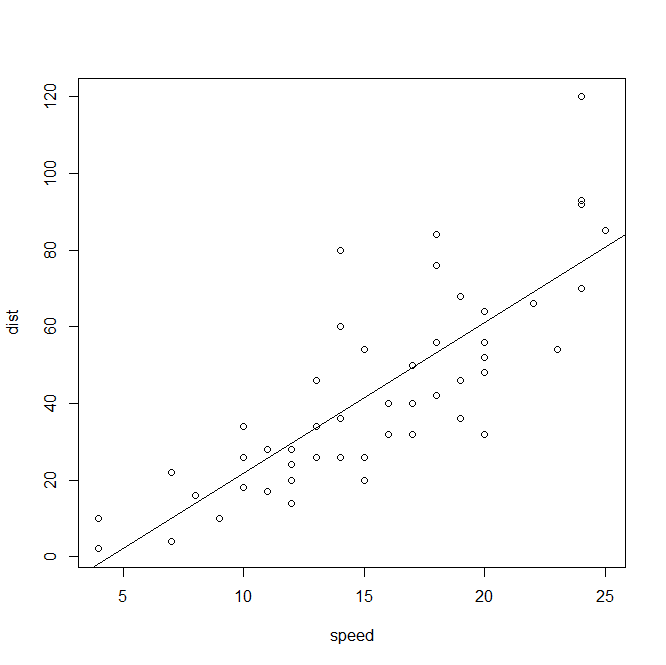
a=lm(dist~speed,data=cars)#线性回归:波浪线左边是自变量,右边是应变量 summary(a)#a的统计指标,可以看到a的各种检验 #Residuals:残差 Coefficients:系数 #p值小于5%说明回归系数显著,p值越小越拒绝原假设,原假设是回归方程不显著 #str(a)#可查看a的结构:列表结构 plot(cars) abline(a)#a的回归直线
结果:
Call: lm(formula = dist ~ speed, data = cars) Residuals: Min 1Q Median 3Q Max -29.069 -9.525 -2.272 9.215 43.201 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -17.5791 6.7584 -2.601 0.0123 * speed 3.9324 0.4155 9.464 1.49e-12 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 15.38 on 48 degrees of freedom Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438 F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
逐步回归:多元回归,很多个自变量,计算AIC统计量越小越好
w=read.table("COfreewy.txt",header=T)
w#24行,4列
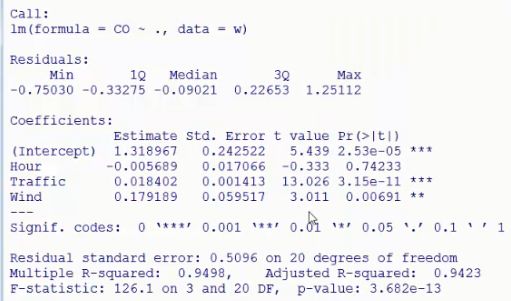
a=lm(CO~.,data=w)#CO作为自变量,其他作为因变量
summary(a)
结果:
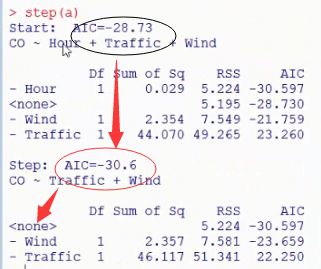
#从上述结果中看出Hour的p值>0.05,不显著,所以可以做逐步回归 step(a) #AIC统计量=-(参数个数+似然函数的对数),越小越好,表示模型的精简程度以及模型的预测准确度
结果:
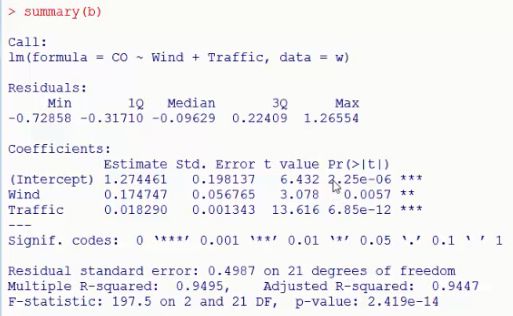
#从上述结果可以看出Hour不参与回归 b=lm(CO~Wind+Traffic,data=w) summary(b)#Wind和Traffic都很显著
结果:
八、R语言可视化(推荐R绘图系统)
1.散点图,折线图,垂线图 plot()
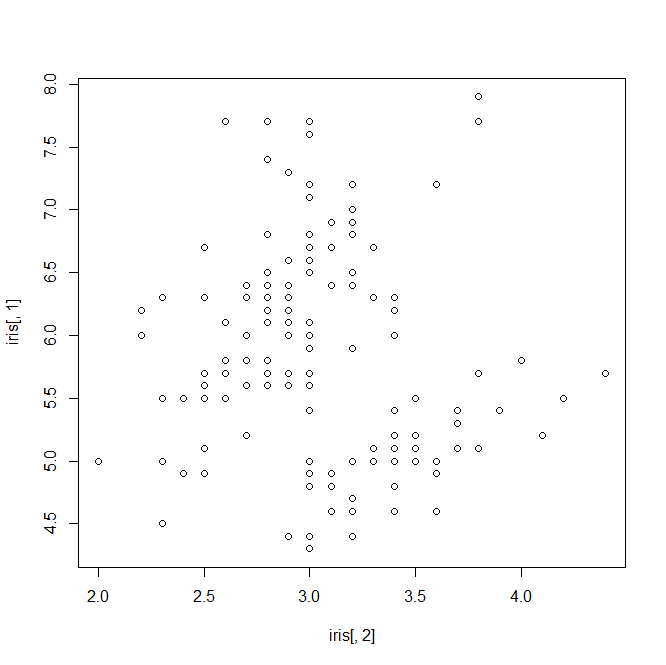
iris str(iris)#Species:Factor(分类变量,也叫因子变量)为非数值,会被编码,第一个出现的类别会被编码成1 plot(iris[,2],iris[,1])#散点图
结果:
> iris Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa 7 4.6 3.4 1.4 0.3 setosa 8 5.0 3.4 1.5 0.2 setosa 9 4.4 2.9 1.4 0.2 setosa 10 4.9 3.1 1.5 0.1 setosa 11 5.4 3.7 1.5 0.2 setosa 12 4.8 3.4 1.6 0.2 setosa 13 4.8 3.0 1.4 0.1 setosa 14 4.3 3.0 1.1 0.1 setosa 15 5.8 4.0 1.2 0.2 setosa 16 5.7 4.4 1.5 0.4 setosa 17 5.4 3.9 1.3 0.4 setosa 18 5.1 3.5 1.4 0.3 setosa 19 5.7 3.8 1.7 0.3 setosa 20 5.1 3.8 1.5 0.3 setosa 21 5.4 3.4 1.7 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 23 4.6 3.6 1.0 0.2 setosa 24 5.1 3.3 1.7 0.5 setosa 25 4.8 3.4 1.9 0.2 setosa 26 5.0 3.0 1.6 0.2 setosa 27 5.0 3.4 1.6 0.4 setosa 28 5.2 3.5 1.5 0.2 setosa 29 5.2 3.4 1.4 0.2 setosa 30 4.7 3.2 1.6 0.2 setosa 31 4.8 3.1 1.6 0.2 setosa 32 5.4 3.4 1.5 0.4 setosa 33 5.2 4.1 1.5 0.1 setosa 34 5.5 4.2 1.4 0.2 setosa 35 4.9 3.1 1.5 0.2 setosa 36 5.0 3.2 1.2 0.2 setosa 37 5.5 3.5 1.3 0.2 setosa 38 4.9 3.6 1.4 0.1 setosa 39 4.4 3.0 1.3 0.2 setosa 40 5.1 3.4 1.5 0.2 setosa 41 5.0 3.5 1.3 0.3 setosa 42 4.5 2.3 1.3 0.3 setosa 43 4.4 3.2 1.3 0.2 setosa 44 5.0 3.5 1.6 0.6 setosa 45 5.1 3.8 1.9 0.4 setosa 46 4.8 3.0 1.4 0.3 setosa 47 5.1 3.8 1.6 0.2 setosa 48 4.6 3.2 1.4 0.2 setosa 49 5.3 3.7 1.5 0.2 setosa 50 5.0 3.3 1.4 0.2 setosa 51 7.0 3.2 4.7 1.4 versicolor 52 6.4 3.2 4.5 1.5 versicolor 53 6.9 3.1 4.9 1.5 versicolor 54 5.5 2.3 4.0 1.3 versicolor 55 6.5 2.8 4.6 1.5 versicolor 56 5.7 2.8 4.5 1.3 versicolor 57 6.3 3.3 4.7 1.6 versicolor 58 4.9 2.4 3.3 1.0 versicolor 59 6.6 2.9 4.6 1.3 versicolor 60 5.2 2.7 3.9 1.4 versicolor 61 5.0 2.0 3.5 1.0 versicolor 62 5.9 3.0 4.2 1.5 versicolor 63 6.0 2.2 4.0 1.0 versicolor 64 6.1 2.9 4.7 1.4 versicolor 65 5.6 2.9 3.6 1.3 versicolor 66 6.7 3.1 4.4 1.4 versicolor 67 5.6 3.0 4.5 1.5 versicolor 68 5.8 2.7 4.1 1.0 versicolor 69 6.2 2.2 4.5 1.5 versicolor 70 5.6 2.5 3.9 1.1 versicolor 71 5.9 3.2 4.8 1.8 versicolor 72 6.1 2.8 4.0 1.3 versicolor 73 6.3 2.5 4.9 1.5 versicolor 74 6.1 2.8 4.7 1.2 versicolor 75 6.4 2.9 4.3 1.3 versicolor 76 6.6 3.0 4.4 1.4 versicolor 77 6.8 2.8 4.8 1.4 versicolor 78 6.7 3.0 5.0 1.7 versicolor 79 6.0 2.9 4.5 1.5 versicolor 80 5.7 2.6 3.5 1.0 versicolor 81 5.5 2.4 3.8 1.1 versicolor 82 5.5 2.4 3.7 1.0 versicolor 83 5.8 2.7 3.9 1.2 versicolor 84 6.0 2.7 5.1 1.6 versicolor 85 5.4 3.0 4.5 1.5 versicolor 86 6.0 3.4 4.5 1.6 versicolor 87 6.7 3.1 4.7 1.5 versicolor 88 6.3 2.3 4.4 1.3 versicolor 89 5.6 3.0 4.1 1.3 versicolor 90 5.5 2.5 4.0 1.3 versicolor 91 5.5 2.6 4.4 1.2 versicolor 92 6.1 3.0 4.6 1.4 versicolor 93 5.8 2.6 4.0 1.2 versicolor 94 5.0 2.3 3.3 1.0 versicolor 95 5.6 2.7 4.2 1.3 versicolor 96 5.7 3.0 4.2 1.2 versicolor 97 5.7 2.9 4.2 1.3 versicolor 98 6.2 2.9 4.3 1.3 versicolor 99 5.1 2.5 3.0 1.1 versicolor 100 5.7 2.8 4.1 1.3 versicolor 101 6.3 3.3 6.0 2.5 virginica 102 5.8 2.7 5.1 1.9 virginica 103 7.1 3.0 5.9 2.1 virginica 104 6.3 2.9 5.6 1.8 virginica 105 6.5 3.0 5.8 2.2 virginica 106 7.6 3.0 6.6 2.1 virginica 107 4.9 2.5 4.5 1.7 virginica 108 7.3 2.9 6.3 1.8 virginica 109 6.7 2.5 5.8 1.8 virginica 110 7.2 3.6 6.1 2.5 virginica 111 6.5 3.2 5.1 2.0 virginica 112 6.4 2.7 5.3 1.9 virginica 113 6.8 3.0 5.5 2.1 virginica 114 5.7 2.5 5.0 2.0 virginica 115 5.8 2.8 5.1 2.4 virginica 116 6.4 3.2 5.3 2.3 virginica 117 6.5 3.0 5.5 1.8 virginica 118 7.7 3.8 6.7 2.2 virginica 119 7.7 2.6 6.9 2.3 virginica 120 6.0 2.2 5.0 1.5 virginica 121 6.9 3.2 5.7 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 123 7.7 2.8 6.7 2.0 virginica 124 6.3 2.7 4.9 1.8 virginica 125 6.7 3.3 5.7 2.1 virginica 126 7.2 3.2 6.0 1.8 virginica 127 6.2 2.8 4.8 1.8 virginica 128 6.1 3.0 4.9 1.8 virginica 129 6.4 2.8 5.6 2.1 virginica 130 7.2 3.0 5.8 1.6 virginica 131 7.4 2.8 6.1 1.9 virginica 132 7.9 3.8 6.4 2.0 virginica 133 6.4 2.8 5.6 2.2 virginica 134 6.3 2.8 5.1 1.5 virginica 135 6.1 2.6 5.6 1.4 virginica 136 7.7 3.0 6.1 2.3 virginica 137 6.3 3.4 5.6 2.4 virginica 138 6.4 3.1 5.5 1.8 virginica 139 6.0 3.0 4.8 1.8 virginica 140 6.9 3.1 5.4 2.1 virginica 141 6.7 3.1 5.6 2.4 virginica 142 6.9 3.1 5.1 2.3 virginica 143 5.8 2.7 5.1 1.9 virginica 144 6.8 3.2 5.9 2.3 virginica 145 6.7 3.3 5.7 2.5 virginica 146 6.7 3.0 5.2 2.3 virginica 147 6.3 2.5 5.0 1.9 virginica 148 6.5 3.0 5.2 2.0 virginica 149 6.2 3.4 5.4 2.3 virginica 150 5.9 3.0 5.1 1.8 virginica > str(iris)#Species:Factor(分类变量,也叫因子变量)为非数值,会被编码,第一个出现的类别会被编码成1 'data.frame': 150 obs. of 5 variables: $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
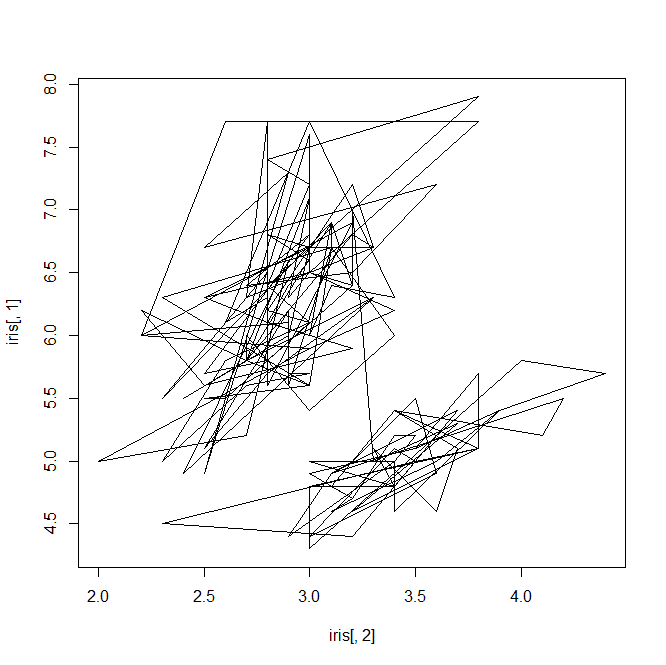
plot(iris[,2],iris[,1],type='l')#折线图
结果:
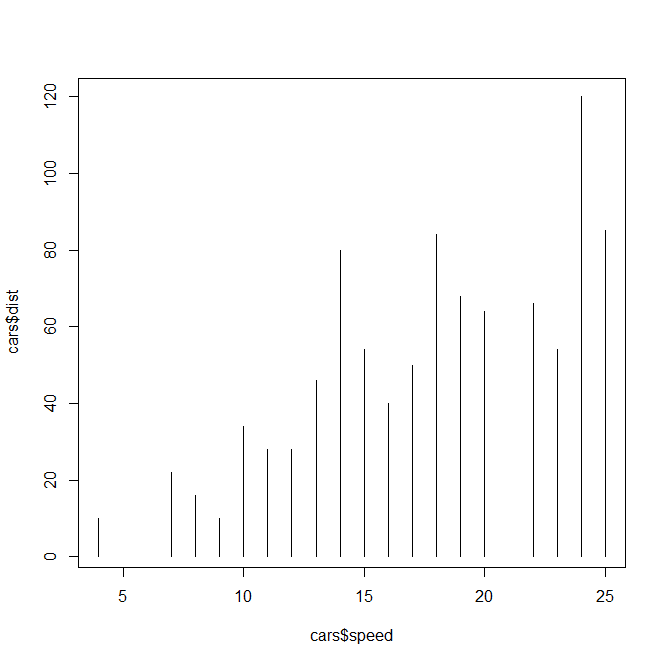
plot(cars$speed,cars$dist,type='h')#垂线图
结果:
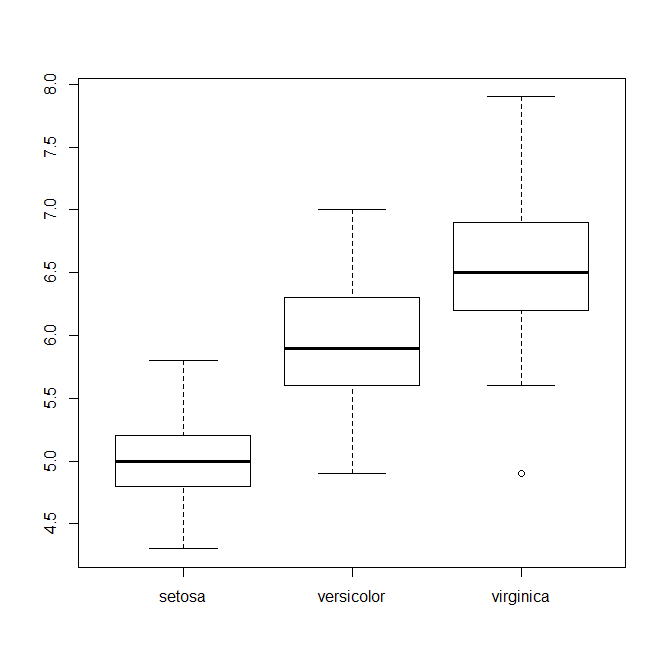
plot(iris[,5],iris[,1])#盒装图(5个分位点:最大值,最小值,中位点,25%,75%分位点) iris[,5]非数值 #盒装图作用是比较不同种类的中位数
结果:
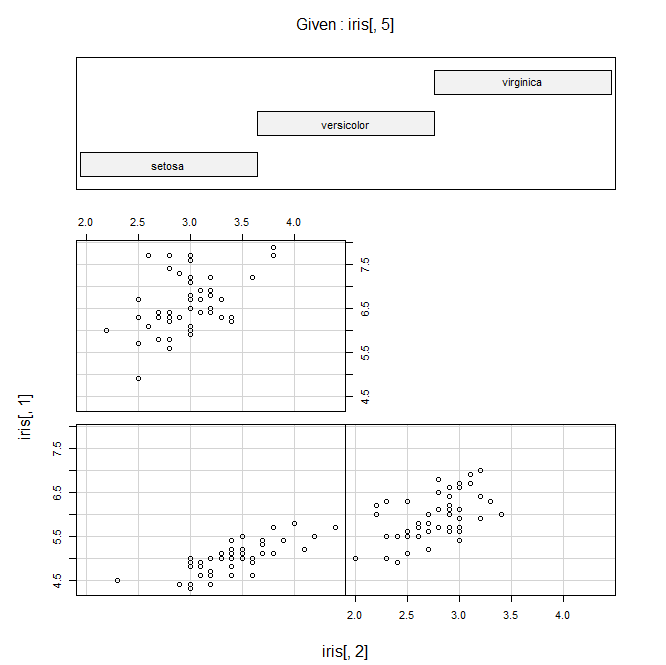
#以第五列分类,画第一列和第二列构成的散点图 coplot(iris[,1]~iris[,2]|iris[,5])#分类画图
结果:
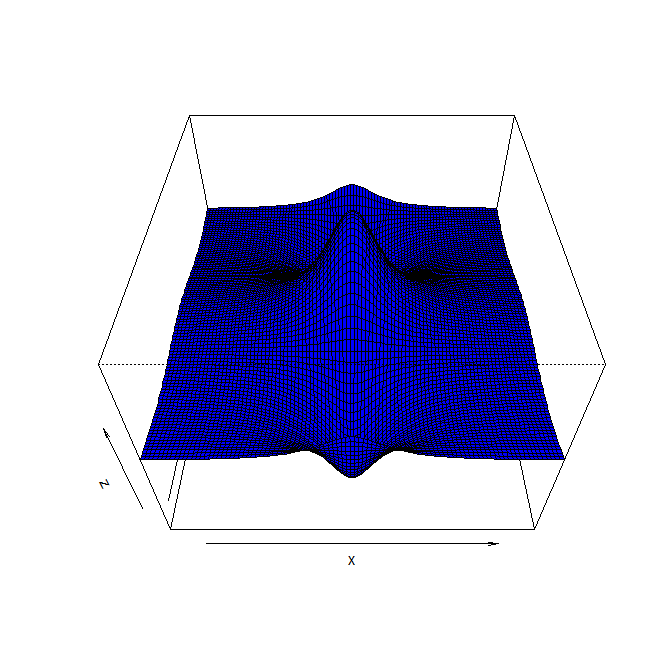
2 三维图像 perp() 两个自变量
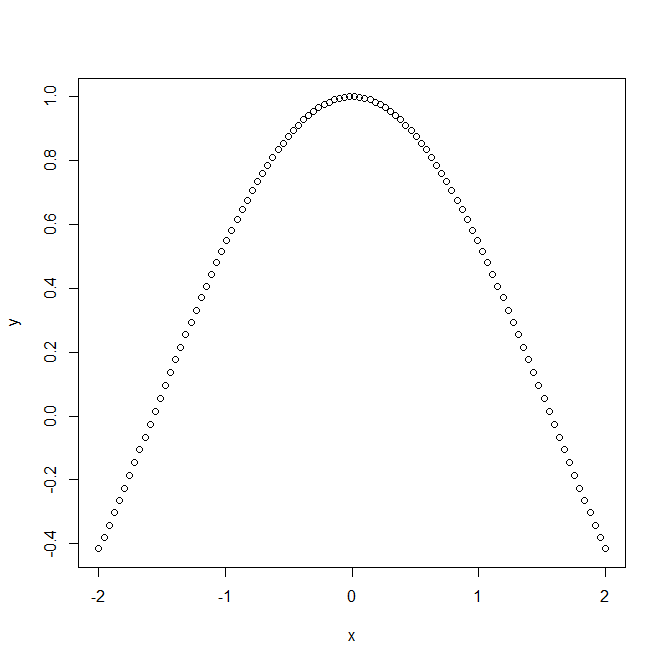
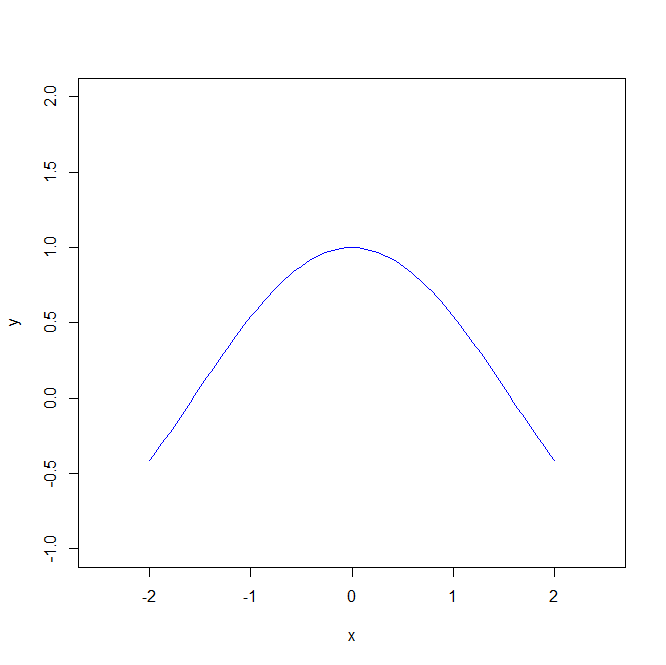
z=cos(y)/(1+x^2) x=seq(-2,2,len=100) y=cos(x) #二维图像 plot(x,y) plot(y~x,type="l",xlim=c(-2.5,2.5),ylim=c(-1,2),col='blue')
结果:
x=seq(-5,5,len=100)
y=seq(-5,5,len=100)
f=function(x,y){cos(y)/(1+x^2)}
z=outer(x,y,f)#必须定义一个函数,z经过x和y的外积求值
#三维图像
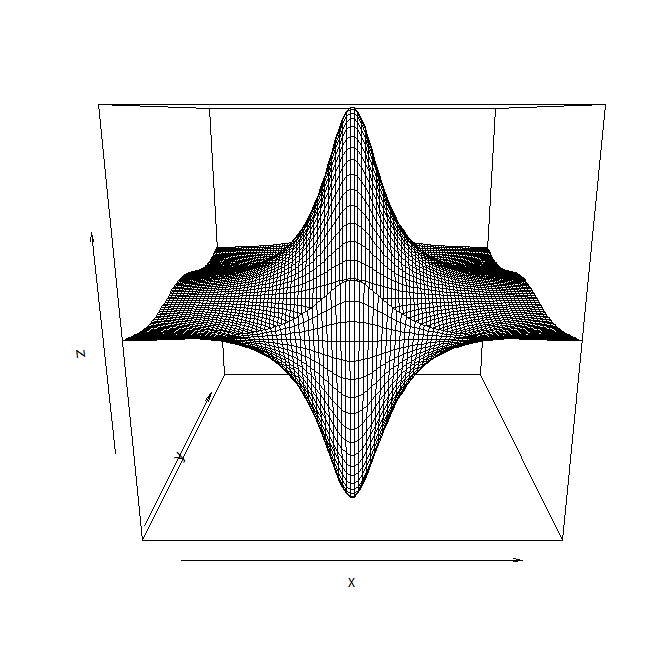
persp(x,y,z)
persp(x,y,z,thete=30,phi=45,col='blue',expand=0.7)#expand拉长0.7倍,thete和phi用于调整角度
结果:
3 双纵轴图像:经济领域
#1912年开始,每年中每个季度喝醉酒的人数 drunkenness=ts(c(3875,4846,5128,8773,7327, 6688,5582,3473,3196, rep(NA,51)),frequency=4,start=1912)#frequency=4,表示4个数代表1年的数,即1个数代表1个季度的值 drunkenness
结果:
> drunkenness Qtr1 Qtr2 Qtr3 Qtr4 1912 3875 4846 5128 8773 1913 7327 6688 5582 3473 1914 3196 NA NA NA 1915 NA NA NA NA 1916 NA NA NA NA 1917 NA NA NA NA 1918 NA NA NA NA 1919 NA NA NA NA 1920 NA NA NA NA 1921 NA NA NA NA 1922 NA NA NA NA 1923 NA NA NA NA 1924 NA NA NA NA 1925 NA NA NA NA 1926 NA NA NA NA
#1912年开始,每年喝醉酒的人数 drunkenness=ts(c(3875,4846,5128,8773,7327, 6688,5582,3473,3196, rep(NA,51)),start=1912)#51个缺省值,ts表示时间序列,frequency默认为1,1个数代表1年的值 drunkenness
结果:
> drunkenness Time Series: Start = 1912 End = 1971 Frequency = 1 [1] 3875 4846 5128 8773 7327 6688 5582 3473 3196 NA NA NA NA NA [15] NA NA NA NA NA NA NA NA NA NA NA NA NA NA [29] NA NA NA NA NA NA NA NA NA NA NA NA NA NA [43] NA NA NA NA NA NA NA NA NA NA NA NA NA NA [57] NA NA NA NA
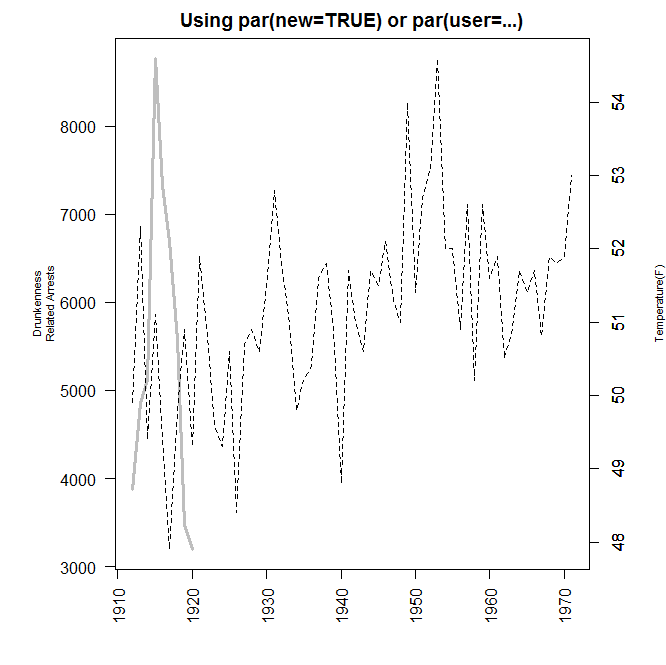
par(mar=c(5,6,2,4))#par图形设备参数设置,mar指的是与各边框的距离
plot(drunkenness,lwd=3,col='gray',ann=F,las=2)#lwd指的是线宽,gray是灰色,las表示刻度文本方向(可更改为1),ann指的是横纵轴以及标题(T,F,TRUE,FALSE四个取值)
mtext("Drunkenness\nRelated Arrests",side=2,line=3,cex=0.7)#空白处文本,side与line表示调整距离,cex(默认等于1)表示文本大小,0.7为70%大小
#高级绘图函数不能叠加高级绘图函数,可以叠加低级绘图函数,但是设置下式则可以
par(new=TRUE)#纵轴坐标的取值范围长短可能会改变
plot(nhtemp,ann=False,axes=FALSE,lwd=0.6,lty=2)#axes=FALSE表示所有轴都不画,lty默认值为1表示实线(2,3为虚线)
mtext("Temperature(F)",side=4,line=3,cex=0.7)
title('Using par(new=TRUE) or par(user=...)')#标题
axis(4)#右边的轴,与第二个图相关联
结果:
4 饼状图
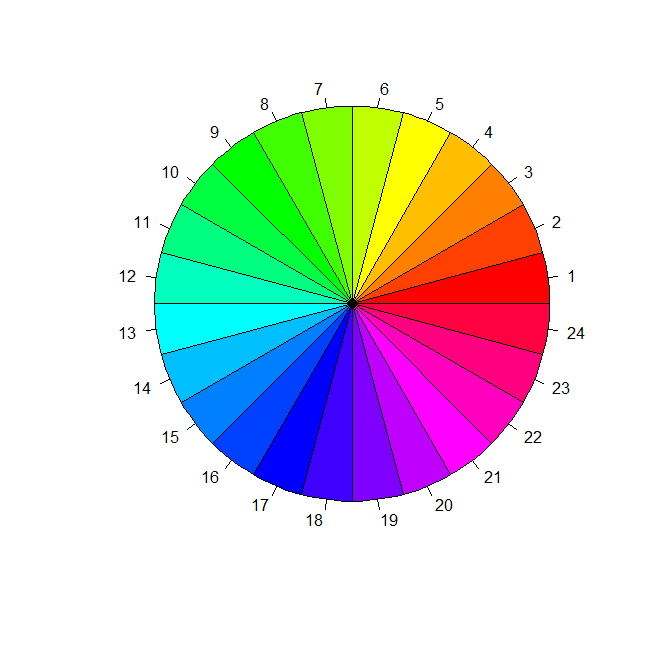
?pie
pie(rep(1, 24), col = rainbow(24), radius = 0.9)#rep(1, 24)将1重复24遍,是个24维向量。radius半径
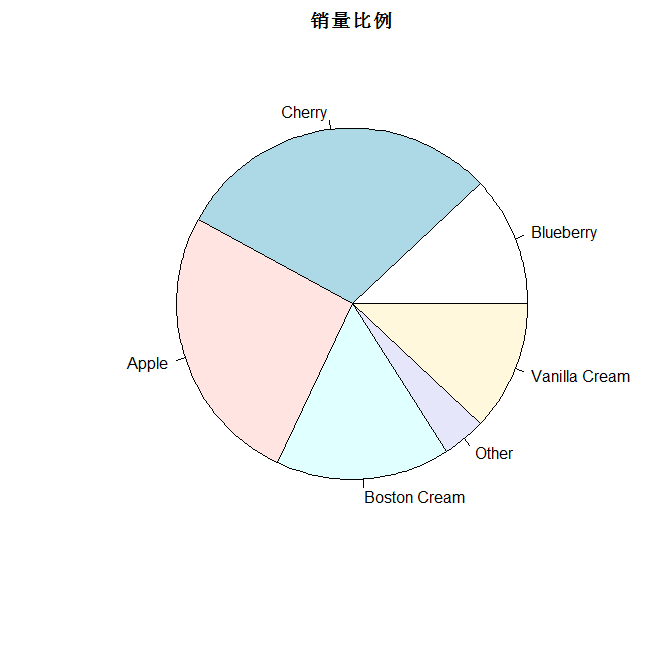
sales = c(0.12, 0.3, 0.26, 0.16, 0.04, 0.12)
names(sales) = c("Blueberry", "Cherry",
"Apple", "Boston Cream", "Other", "Vanilla Cream")#给数据框的每一列命名
title('销量比例')
pie(sales) # default colours
结果:
5 条状图(常和双纵轴图像配合)
?barplot
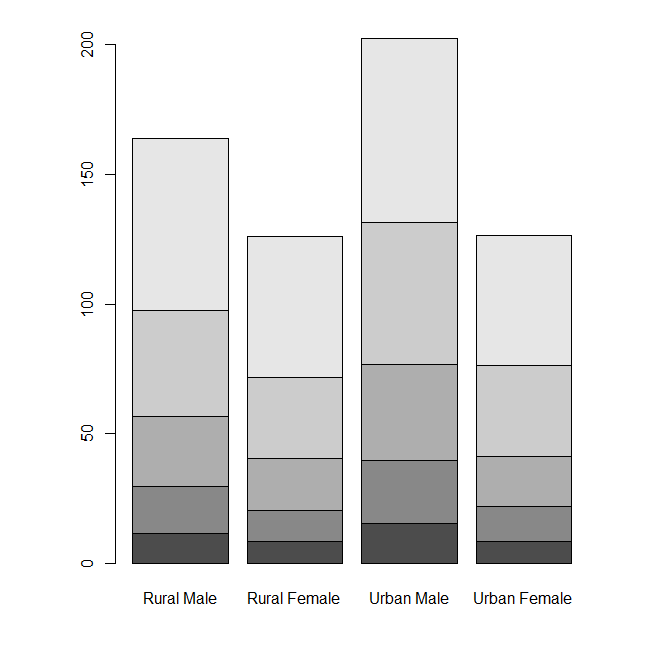
VADeaths#某地区死亡率
str(VADeaths)#格式均为数值型 num [1:5, 1:4] 11.7 18.1 26.9 41 66 8.7 11.7 20.3 30.9 54.3 ...
#第一个图
barplot(VADeaths)
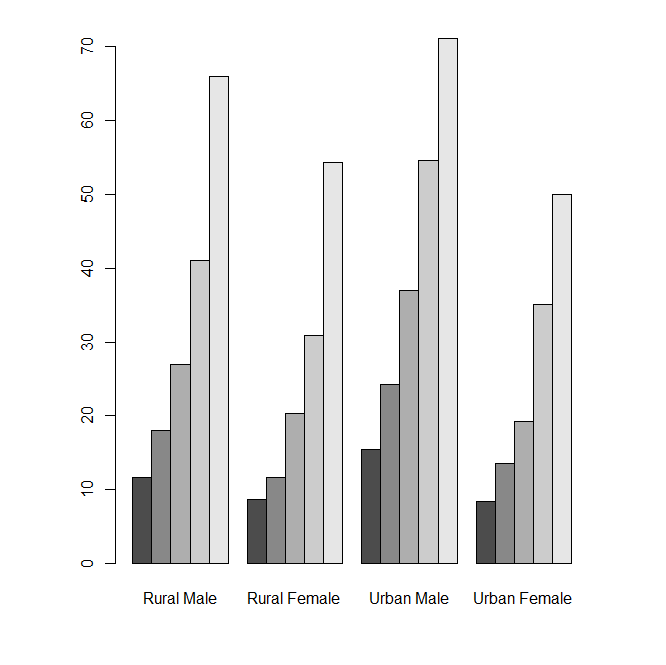
#第二个图
barplot(VADeaths, beside = TRUE)
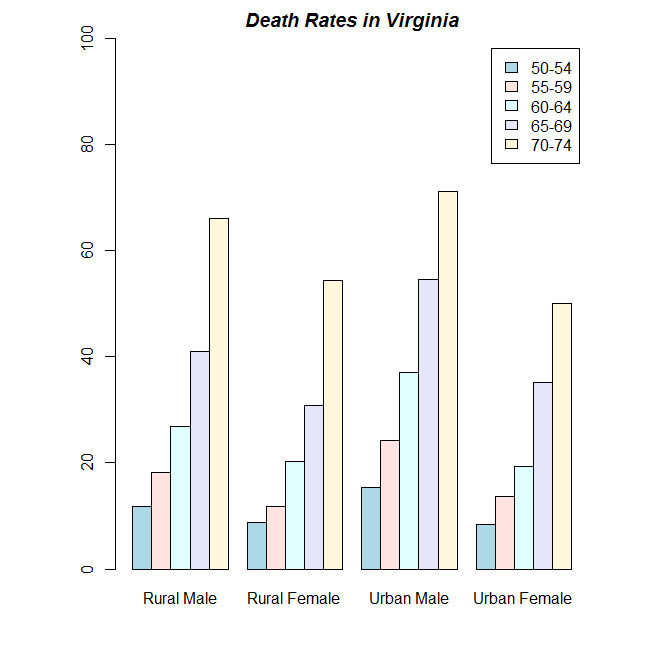
#第三个图
barplot(VADeaths, beside = TRUE,
col = c("lightblue", "mistyrose", "lightcyan",
"lavender", "cornsilk"),
legend = rownames(VADeaths), ylim = c(0, 100))
title(main = "Death Rates in Virginia", font.main = 4)
结果:
> VADeaths Rural Male Rural Female Urban Male Urban Female 50-54 11.7 8.7 15.4 8.4 55-59 18.1 11.7 24.3 13.6 60-64 26.9 20.3 37.0 19.3 65-69 41.0 30.9 54.6 35.1 70-74 66.0 54.3 71.1 50.0 > str(VADeaths) num [1:5, 1:4] 11.7 18.1 26.9 41 66 8.7 11.7 20.3 30.9 54.3 ... - attr(*, "dimnames")=List of 2 ..$ : chr [1:5] "50-54" "55-59" "60-64" "65-69" ... ..$ : chr [1:4] "Rural Male" "Rural Female" "Urban Male" "Urban Female"
6 ggplot2包,qplol()--------自学
#补充:
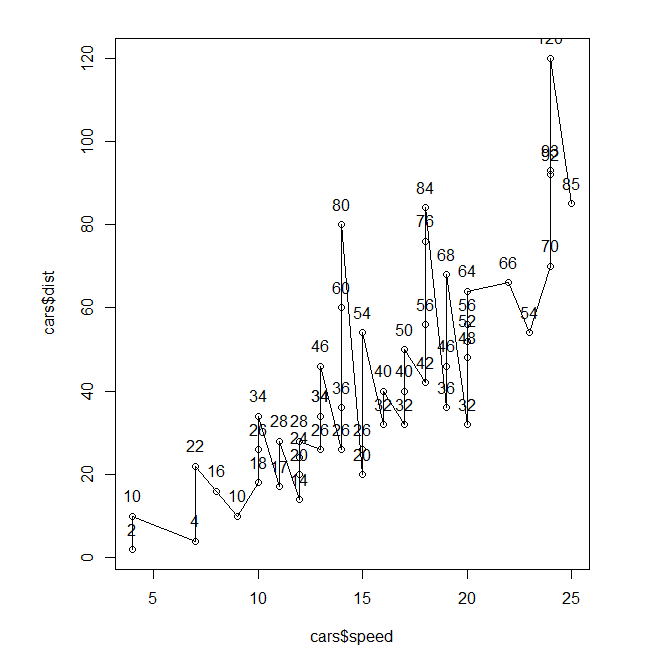
plot(cars$speed,cars$dist,type='o')
#text()函数可以在每个坐标上添加y的取值
for(i in 1:50){
text(cars[i,1],cars[i,2]+5,cars[i,2])
}#+5代表向上一点,不用和点重合了,加多少都行,主要为了好看
结果:
感谢天津商业大学的刘东老师:
书本推荐:薛毅的书,当工具书看,用到哪里查哪里,上边的都可以查到
画图的话,推荐R绘图系统,当工具书使用,用到哪里查哪里