Python之粒子群算法(含代码实例)
这个算法,咋一听感觉很高级,挺难的,其实学习过后也就那样,原理其实挺简单的。下面是我对粒子群算法的一些个人理解,如有差错,还望指出。
一、粒子群算法简介
Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法,自然界中各种生物体均具有一定的群体行为,而人工生命的主要研究领域之一是探索自然界生物的群体行为,从而在计算机上构建其群体模型。
二、粒子群算法原理
它的原理简单来说就是设置一群的粒子在空间里帮你找那个最理想的值。问题的关键就在于这群粒子是怎么找的呢??
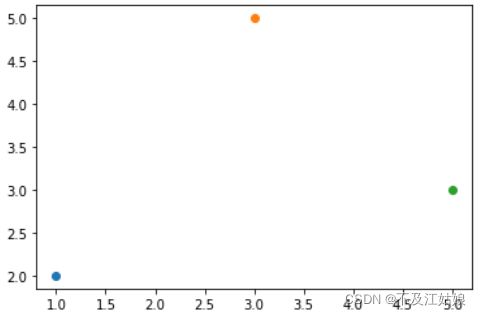
我们看到这副图,我们假设蓝色的点是最理想的点(设它为b点,坐标为(1,2)),然后橙色的点和绿色的点是我们的派出去的“小兵”,要让它们来帮我们找到那个最理想的点(设它们分别为o点(3,5),g点(5,3))。OK,现在这两“小兵”收到消息,知道了最理想的点在b(1,2),那它是不是就要去往这个点靠啊,但是呢,这个“小兵”它也有自己的想法(以o(3,5)为例),比如说:
一开始的这个“小兵"o点,它觉得最理想的点应该是在它的左边(红色箭头),但它收到消息,同伴找到了一个最理想的点了——b点(绿色箭头方向),b点是所以”小兵“公认的最理想的,我们管它叫全局最优,但“小兵o”仍然怀疑b点可能不是最理想的,它仍然认为最理想的点是在红色箭头的方向,可是它又不排除b点或许就是最理想的点,所以呢,它就会选一个折中的方向去寻找这个最理想的点,所以它就选择了黄色箭头这条路去找。
我们接着来看,每个”小兵“,从当前的位置到另一个位置的移动,是有大小的,也是有方向的,而这种有大小又有方向的东西,我们就叫它向量。所以我们也可以用向量来表示每个”小兵“。
如果我投放了很多个”小兵“,它们都有这样的想法,那我们对这个空间的搜索是不是就非常的高效啊,那就可以充分的挖掘出整个空间上的信息。
那接下来,我们将这种原理用数学将它抽象化。
三、粒子群算法数学公式
假设在一个D维的目标搜索空间中,有N个粒子(也就是上述的小兵)组成一个群落,其中第i个粒子表示为一个D维的向量:
![]()
比如上述的o点,在二维空间就表示为(3,5)
第i粒子的”速度“(也可以看作每一个小兵,朝某个方向移动的时候的步子的大小)也是一个D维的向量,记为:(在这里,这个公式大家先了解它的含义就可以了,等会我会告诉大家怎么得到它)
注意:这个“速度”也是向量,它有大小也有方向
![]()
在第t代的第i个粒子向第t+1代进化时,根据如下式子更新:
这个公式的意思就是,我们将每个粒子迭代,寻找了一代之后,计算一下谁的点更理想,再对每个粒子进行位置的更新,这个更新,就是在你原来的位置上加上你走的”步子“。通过这样的方式,从而不断的发现更好的点。
而这位置更新的关键就是后面的”速度“,它要怎么得到呢?它的大小和方向如何确定?
![]()
我们通过这个公式来确定”速度“,首先,我们来看,它有三个项。
第一个项里的![]() 是粒子第t代的“速度”,而前面的参数
是粒子第t代的“速度”,而前面的参数![]() 你可以看作是一个参数,由你自己设定,我们叫它惯性权重。那这是什么意思呢? 其实这是一种“惯性”的思想,我们来看下面的图:
你可以看作是一个参数,由你自己设定,我们叫它惯性权重。那这是什么意思呢? 其实这是一种“惯性”的思想,我们来看下面的图: 
对于C点,它个体认为最理想的点是B点,但其他的粒子认为最理想的是A点,受个体和全局的影响,所以它最后是往黄色箭头方向走,这个箭头就是在第t代时候的“速度”,第一项这个“惯性”指的就是黄色箭头的方向。
第二项,我们先看括号里的![]() ,这里的
,这里的![]() 指的是粒子在第t代时,在它初始的方向上找的最理想的点,
指的是粒子在第t代时,在它初始的方向上找的最理想的点,![]() 指的就是第t代时,当前粒子的位置,它们相减不就得到了粒子到个体认为是最理想点的向量了吗,也就是图中绿色的箭头。
指的就是第t代时,当前粒子的位置,它们相减不就得到了粒子到个体认为是最理想点的向量了吗,也就是图中绿色的箭头。
我第一项加上第二项,就得到了图中黑色的箭头方向。
第三个项,![]() ,这里的
,这里的![]() 指的是在第t代的时候,全部粒子认为它是最理想的点,那它减去我们当前的位置,不就得到了粒子到全局最理想点的向量了吗,也就是图中红色的箭头。
指的是在第t代的时候,全部粒子认为它是最理想的点,那它减去我们当前的位置,不就得到了粒子到全局最理想点的向量了吗,也就是图中红色的箭头。
前面两个项相加得到的黑色箭头再加上红色箭头就得到了蓝色的箭头,而这蓝色的箭头就是我们第t+1代的“速度”。
而第二个项和第三个项前面的![]() 和
和![]() 就是两个随机数,
就是两个随机数,![]() 和
和![]() 是两个参数,c1是个体的学习系数,c2是全局的学习系数。
是两个参数,c1是个体的学习系数,c2是全局的学习系数。
(其实对于这两个学习系数和惯性权重,如果它们是一个定值,是很不妥的,因为,如果是在第10代,你希望的是更大的遍历整个空间,找到最理想的值,而不是尽量往,第10代找到的最理想值靠,所以你的系数c1和权重w在前期应该要大些,c2要小些。到了第900代,粒子在自己的方向仍然没有找到比现有的最理想值更理想,所以这个时候,就得尽量往全局最理想的值上面靠,所以你的系数c1和权重w就应该小些,c2就应该大些了。具体怎么改进,我在这里就没有提到了,大家有兴趣可以自己去了解一下改进方法)
四、粒子群算法步骤
1.初始化种群x。就是让你派出去“小兵”,将它们随机扔在空间里。
2.计算个体适应度。这一步就是计算你每一个“小兵”找到的点是否接近你要的最理想的值,越接近,适应度越高。
3.更新粒子速度和粒子的位置。注意:在更新速度之前要进行速度边界检测,一般是当v>v(max)的时v=(max)。这么做的目的,是担心速度太大,一下就错过了本该是最理想的点。
4.计算新位置的适应度,如果新位置适应度更高,则将该粒子的位置进行更新,否则就不更新。
5.判断是否满足终止条件,满足就退出,不满足就返回第二步继续迭代。终止条件一般为迭代的次数,或者适应度不再变化等。
五、代码实例
#f(x,y) = x^2 + y^2 + x
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D#导入该函数是为了绘制3D图
import matplotlib as mpl
#########
#将数据绘图出来
#生成X和Y的数据
X = np.arange(-5,5,0.1) #-5到5的等距数组,距离为0.1,注意区分开range(),它返回的是一个列表
Y = np.arange(-5,5,0.1)
X,Y = np.meshgrid(X,Y)#该函数用来生成网格点坐标矩阵。
#目标函数
Z = X**2 + Y**2 + X
#绘图
fig = plt.figure()#创立一个画布
ax = Axes3D(fig)#在这个画布里,生成一个三维的空间
surf = ax.plot_surface(X,Y,Z,cmap=cm.coolwarm)#该函数是为了将数据在这三维空间里可视化出来。
plt.show()
###########
#######
#计算适应度,这里的适应度就是我们目标函数Z的值,因为我们要求Z的最小值。
#这两个函数,一般使用mpl画图的时候都会用到
mpl.rcParams['font.sans-serif'] = ['SimHei']# 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'无法显示的问题
#使用matplotliblib画图的时候经常会遇见中文或者是负号无法显示的情况
#rcParams函数里的参数可以修改默认的属性,包括窗体大小、每英寸的点数、线条宽度、颜色、样式、坐标轴、坐标和网络属性、文本、字体等
def fitness_func(X):
x = X[:,0]
y = X[:,1]
return x**2 + y**2 + x
##########
#############
#更新速度,根据公式V(t+1)=w*V(t)+c1*r1*(pbest_i-xi)+c1*r1*(gbest_xi)
def velocity_update(V,X,pbest,gbest,c1,c2,w,max_val):
size = X.shape[0]#返回矩阵X的行数
r1 = np.random.random((size,1))#该函数表示成size行 1列的浮点数,浮点数都是从0-1中随机。
r2 = np.random.random((size,1))
V = w*V + c1*r1*(pbest-X)+c2*r2*(gbest-X)#注意这里得到的是一个矩阵
#这里是一个防止速度过大的处理,怕错过最理想值
V[V<-max_val] = -max_val
V[V>-max_val] = max_val
return V
#########
########
#更新粒子位置,根据公式X(t+1)=X(t)+V
def position_updata(X,V):
return X+V
##########
#########
def pos():
w = 1 #设置惯性权重
c1 = 2 #设置个体学习系数
c2 = 2 #设置全局学习系数
r1 = None
r2 = None
dim = 2
size = 20 #这里是初始化粒子群,20个
iter_num = 1000 #迭代1000次
max_val = 0.5 #限定最大速度为0.5
best_fitness = float(9e10) #初始化适应度的值
fitness_val_list = []
#初始化各个粒子的位置
X = np.random.uniform(-5,5,size=(size,dim))
#初始化各个粒子的速度
V = np.random.uniform(-0.5,0.5,size=(size,dim))
p_fitness = fitness_func(X)#得到各个个体的适应度值
g_fitness = p_fitness.min()#全局最理想的适应度值
fitness_val_list.append(g_fitness)
pbest = X#初始化个体的最优位置
gbest = X[p_fitness.argmin()]#初始化整个整体的最优位置
#迭代
for i in range(1,iter_num):
V = velocity_update(V, X, pbest, gbest, c1, c2, w, max_val)
X = position_updata(X,V)
p_fitness2 = fitness_func(X)
g_fitness2 = p_fitness2.min()
#更新每个粒子的历史的最优位置
for j in range(size):
if p_fitness[j] > p_fitness2[j]:
pbest[j] = X[j]
p_fitness[j] = p_fitness2[j]
if g_fitness > g_fitness2:
gbest = X[p_fitness2.argmin()]
g_fitness = g_fitness2
fitness_val_list.append(g_fitness)
i += 1
print("最优值是:%.5f" % fitness_val_list[-1])
print("最优解是:x=%.5f,y=%.5f" % (gbest[0],gbest[1]))
plt.plot(fitness_val_list,c='r')
plt.title('迭代过程')
plt.show()
#########
if __name__ == '__main__':
pos()注:该代码并非本人编写,只是小编在原作者的基础上加注了解释,若想查看源码,可以去这个链接:https://blog.csdn.net/a_hui_tai_lang/article/details/119877370