大力飞砖之暴力解法（上）

前言

暴力算法，你永远可以相信，理论上一定有解的方案，之所以要说这个主要是做一个小总结，还有就是，俺们可以优化这玩意嘛，在没有办法直接想到最优解的情况下，俺们可以慢慢滴从暴力进行优化为贪心,dp。在时间不够的情况下，绝对能够保证你能够过一定量的测试集。当然还有一种就是需要直接去模拟过程的题目，就比如以前做过的Nim游戏，n%4就可以直接判断能不能赢，但实际上怎么来的，做题的时候，你真的能够直接推出来？简单一点是可以，复杂一点呢？

那么咱们这个暴力呢，基本上是分两个常见的，一个就是回溯，然后就是递归嘛，当然主要还是递归，回溯无非是多了几个步骤。

全排列

之所以一来就说这个玩意，主要原因，就是因为，咱们这个比较金典嘛，然后这个写法也是这个比较典型的套路，按照这个套路走比较容易写出那个暴力回溯，DFS，BFS的代码。
而且其实这个DFS是那啥直接递归的优化，然后BFS又是对DFS的再次优化（针对最优求解的问题的时候），后面还不行就dp了呗，还不行那就在对dp搞优化呗，还不行，那就看看有没有特定的公式。

那么这个全排列咧，在这个执行的过程当中，可以画一个是树，不过这个不重要，那玩意不好用。在写全排列，或者别的递归函数的递归层的时候，直接先抽象化一层，因为本身，这个和递归有关的东西，那就很抽象。

所以我们先来想一下，什么全排列，在你自己手动写这个全排列的时候怎么写滴。

例如{1,2,3} 写个全排列.，怎么搞，不就是那啥，先哪一个开头，按照顺序，就是1，然后在拿一个没有拿的，那就是2,3拿一个
假设拿了2，那么此时就是1,2，然后再拿没有重复的1,2,3拿到了，此时长度等于3，然后拿掉3,再看，放回3就重复了，所以再干掉2，然后也是放回去就重复了，然后，在回到1，此时2已经不行了，拿就放3，然后重复步骤，于是132出来了。然后再来。

所有你就直接得到了，这个图。

然后每次拿一个数例如1,2,3的情景，和1,2,3,4,的情景和1,2的情景是一样的，所以这个时候，你全排列还有一个子步骤，那么此时我就让这个拿数字变成一个方法，那么后面让这个玩意递归。

这里的话，还是直接上代码来的实在一点，就那样很好理解。

import java.util.ArrayList;

class Test001{
 
    static int[] a;

    public static void main(String[] args) {
        a = new int[]{1,2,3};
        ArrayList<Integer> temp = new ArrayList<>();
        boolean[] used = new boolean[a.length];
        allSort(a,temp,used);
    }
    public static void allSort(int [] a,ArrayList<Integer> temp,boolean[] used){
        if(temp.size()==a.length){
            System.out.println(temp);
            return;
        }
        for(int i=0;i<a.length;i++){
            if(used[i]) continue;
            temp.add(a[i]);
            used[i] = true;
            allSort(a,temp,used);
            used[i] = false;
            temp.remove(temp.size()-1);

        }
    }
}

这里还有一个类似的代码，是关于求子集的，求长度为2的子集

import java.util.ArrayList;

class Test001{

    static int[] a;

    public static void main(String[] args) {
        a = new int[]{1,2,3};
        ArrayList<Integer> temp = new ArrayList<>();
        boolean[] used = new boolean[a.length];
        allSort(a,temp,0);
    }
    public static void allSort(int [] a,ArrayList<Integer> temp,int index){
        if(temp.size()==2){
            System.out.println(temp);
            return;
        }
        for(int i=index;i<a.length;i++){

            temp.add(a[i]);

            allSort(a,temp,++index);

            temp.remove(temp.size()-1);

        }
    }
}

皇后问题

气氛烘托到这里，那么就是比较金典的那个，N皇后问题，这里话我直接以LeetCode的N皇后问题为例子了。

这里你先看一下最核心的代码

然后再看一下这个全排列的核心代码

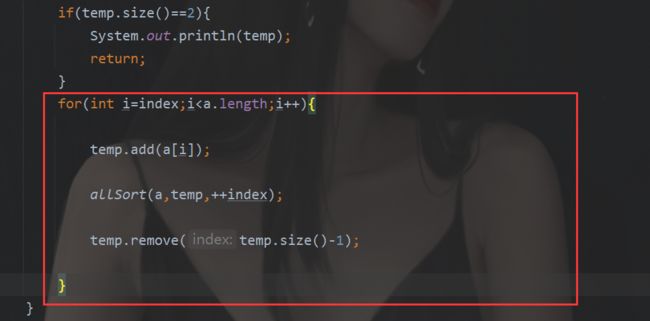
代码结构几乎类似，无非是多了很多的一些输出，输入，判断，格式化方法。
下面是我当时写的题解

题目

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

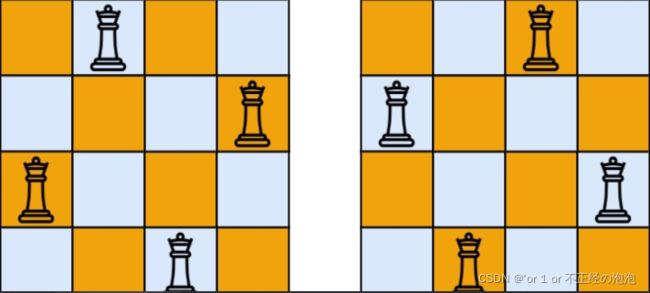
输入：n = 4
输出：[[".Q…","…Q",“Q…”,"…Q."],["…Q.",“Q…”,"…Q",".Q…"]]
解释：如上图所示，4 皇后问题存在两个不同的解法。 示例 2：

输入：n = 1 输出：[[“Q”]]

那么这个 皇后问题其实和我先前做数据结构实训课时候写的迷宫问题的思路其实是类似的，只是我们的规则不一样，先前的迷宫问题使用的DFS的思路，先直接往前走，返现路走不通了，返回，用一个栈来记录走过的路，然后出栈往回走，当然那里用递归也是可以的，不过你也需要用一个栈来存储你走过的路，只是不用循环罢了。
数据结构小设计–（迷宫问题Python版本）

规则

所以明确了我们使用DFS的思想，那么我们来说说这个皇后问题的规则，其实很简单，就是在一个棋盘里面，放置皇后，让皇后互相不能攻击有多少种放置方式。那么皇后攻击的范围如下图。

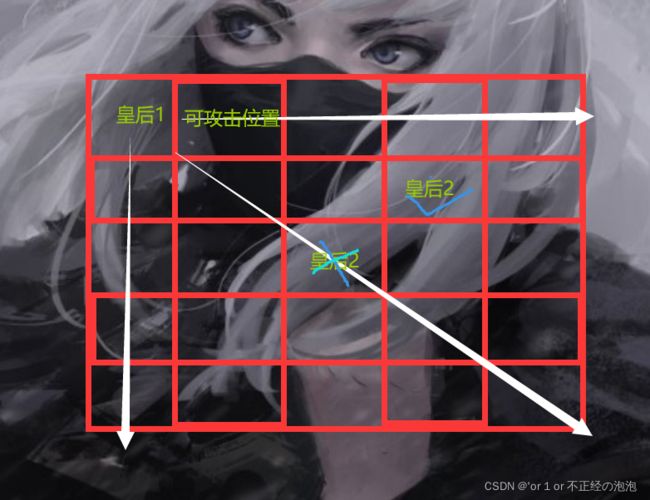
所以我们对于一个要放置的皇后，要保证这个放在的位置在水平，竖直方向，对角线方向上不能有别的皇后。否则就不行。

策略

现在我们已经知道了规则，那么接下来就是我们要大概怎么做。我们这边还是使用最经典的DFS来做一下。首先我们按照行优先嘛，在第一行第一列先试着放一下，然后放第二个，第二个肯定是在第二行，并且不可能在第一列。所以伪代码就出来了。

放置（0,棋盘）//从第0行开始放

放置(j,棋盘){
	for(int i=0;i<列;i++){
		1.终止条件
		
		2.判断能不能放，能放就放并且往下再放
			放置（j+1,棋盘）//往下放第二个
			复原 //假设当前一轮放完了，我们就需要进行“洗牌”
	}
}

这样一来我们就可以不断地去扫描了

判断条件

之后是我们的判断条件，整理有两个注意点，一个是判断当前点是否可以放置，这个我们已经知道了规则，那么就好办了。

放置判断

  public boolean isOk(char[][] chess,int row,int col){
        //列扫描，对角线扫描(上对角，下对角）
        for(int i=0;i<row;i++){
            if(chess[i][col]=='Q'){
                return false;
            }
        }

        for(int i=row-1,j=col-1;i>=0&j>=0;i--,j--){
            if(chess[i][j]=='Q'){
                return false;
            }
        }

        for(int i=row-1,j=col+1;i>=0&&j< chess.length;i--,j++){
            if(chess[i][j]=='Q'){
                return false;
            }
        }

        return true;

    }

我们是行放置的，所以只需要判断列和对角线即可。

找到解的判断

那么之后如何判断我们找到了解。
我们假设是 4 x 4的棋盘，如果第四个放得下去，那么按照逻辑，就会往下一行放，此时传递的行数就是4（从0开始）那么就说明前面的4x4都放好了，如果第四行就放不下去了，那么最多到3。之后我们将我们的结果放进去。

    public void solveN(char[][] chess,int row){
        if(row == chess.length){
            res.add(this.addsolved(chess));
        }
        for(int j=0;j<chess[0].length;j++){
            if(isOk(chess,row,j)){
                chess[row][j] = 'Q';
                solveN(chess,row+1);
                chess[row][j] = '.';//当前一轮结束了，复位
            }
        }
    }

解题代码

那么之后就能解题目了

class Solution {
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char[][] chess = new char[n][n];
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                chess[i][j] = '.';
            }
        }

        solveN(chess,0);

        return res;
    }
    public void solveN(char[][] chess,int row){
        if(row == chess.length){
            res.add(this.addsolved(chess));
        }
        for(int j=0;j<chess[0].length;j++){
            if(isOk(chess,row,j)){
                chess[row][j] = 'Q';
                solveN(chess,row+1);
                chess[row][j] = '.';//当前一轮结束了，复位
            }
        }
    }

    public List<String> addsolved(char[][] chess){
        List<String> res1=new ArrayList<>();
        for(char[] c:chess){
            res1.add(new String(c));
        }
        return res1;
    }

    public boolean isOk(char[][] chess,int row,int col){
        //列扫描，对角线扫描(上对角，下对角）
        for(int i=0;i<row;i++){
            if(chess[i][col]=='Q'){
                return false;
            }
        }

        for(int i=row-1,j=col-1;i>=0&j>=0;i--,j--){
            if(chess[i][j]=='Q'){
                return false;
            }
        }

        for(int i=row-1,j=col+1;i>=0&&j< chess.length;i--,j++){
            if(chess[i][j]=='Q'){
                return false;
            }
        }

        return true;

    }
}

之后还有一个 N皇后问题2，就是叫你返回解的个数，一样的。

搜索问题

这个的话咱们也是直接来个蓝桥杯的例题吧。

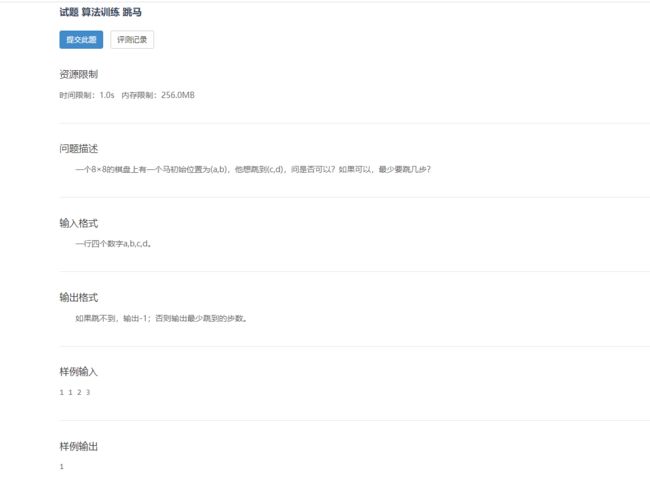
这个题目很好想，直接BFS是吧，看你代码熟不熟，那问题来了，为什么直接BFS是个不错的解法（先不考虑dp），我为什么不用DFS，甚至我都不想用需要剪枝的回溯算法，我直接递归不行嘛。

暴力递归版

这个怎么说，不是放棋子嘛，我就一直放呗，直到我找到了我都最优解，就和先前蓝桥杯 分口罩 2018 java 蓝桥杯B组 第四题，一样是吧。

public class 跳马 {
    //跳跃的步数
    static int minStep = Integer.MAX_VALUE;
    static int count = 0;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int a = scanner.nextInt();
        int b = scanner.nextInt();
        int c = scanner.nextInt();
        int d = scanner.nextInt();
        scanner.close();

        BigInteger bigInteger = BigInteger.valueOf(3);

        //函数调用
        getMin(a,b,c,d);
        System.out.println(minStep==Integer.MAX_VALUE?-1:minStep);
    }

    public static void getMin(int a,int b,int c,int d){
        jump(a,b,c,d,0);
    }

    //jump跳的函数,我们至少是在（1,1）开始的
    public static void jump(int a,int b,int c,int d,int step){
        if(a<1||a>8||b<1||b>8||c<1||c>8||d<1||d>8){
            return;
        }
        if(a==c&&b==d){
            //终止条件
            minStep = Math.min(minStep,step);
            return;
        }
        //栈溢出4234！
        jump(a+1,b-2,c,d,step+1);
        jump(a+2,b-1,c,d,step+1);
        jump(a-1,b-2,c,d,step+1);
        jump(a-2,b-1,c,d,step+1);
        jump(a+2,b+1,c,d,step+1);
        jump(a+1,b+2,c,d,step+1);
        jump(a-1,b+2,c,d,step+1);
        jump(a-2,b+1,c,d,step+1);
        jump(a+2,b-1,c,d,step+1);

    }
}

理论上只要内存大，栈不会溢出（实际上是会溢出的极限值就是4234）就能出答案。（实际上我砍掉了4个方向的递归，测了一下过了3个60分）当然这个想法是直接疯了嘛。

DFS 优化

所以接下来就是啥，是如何转化为DFS进行优化咧，这里的话俺只是，简单说一下思路，因为这个比较简单。

怎么做呢，很简单，就是来个used数组嘛，不过在这里，通俗的叫法叫棋盘呗，你学迷宫问题的时候，或者看前面给到链接，那个python迷宫问题的。那个走过的路标注为1是吧，那么这里也一样，如果在那个里面有标注，那么就不要递归了，你就搞个二维数组，然后先 if(used[a][c]==1) return 是吧。

BFS 优化

这个原来DFS是降低了递归是吧，那么这个BFS也是，再次降低。

import java.util.Scanner;
import java.util.*;
public class Main{

    static  int[][] dir={{1, 2}, {1, -2}, {-1, 2}, {-1, -2}, {2, 1}, {2, -1,}, {-2, 1}, {-2, -1}};
    public static void main(String[] args) {

        System.out.println(bfs());

    }

    private static int bfs() {
        int min=Integer.MAX_VALUE;
        int[][] arr= new int[9][9];
        Scanner scanner = new Scanner(System.in);
        int x1=scanner.nextInt();
        int y1=scanner.nextInt();
        int x2=scanner.nextInt();
        int y2=scanner.nextInt();
        if (x1==x2&&y1==y2) return 0;
        LinkedList<int[]> queue = new LinkedList<>();
        queue.add(new int[]{x1,y1,0});
        arr[x1][y1]=1;

        while (!queue.isEmpty()){
            int[] poll = queue.poll();
            x1=poll[0];
            y1=poll[1];
            if (x1==x2&&y1==y2) break;
            for (int i = 0; i < dir.length; i++) {
                int m=x1+dir[i][0];
                int n=y1+dir[i][1];
                if (m<1||m>8||n<1||n>8){
                    continue;
                }
                if (arr[m][n]==1) continue;
                //符合条件的8个均入队
                queue.addLast(new int[]{m,n,poll[2]+1});
                if (m==x2&&n==y2){
                    min=Math.min(poll[2]+1,min);
                }
            }
        }
        return min;
    }
}

博弈游戏

这部分也是咱们比较那啥。

我们先来个最金典的Nim游戏，按照咱们的暴力的想法。先有这个想法，你再去做解题。明天咱们在专门总结这种“步骤”型的套路和解法。

题目

这个是letcode上滴

你和你的朋友，两个人一起玩 Nim 游戏： 桌子上有一堆石头。 你们轮流进行自己的回合，你作为先手。 每一回合，轮到的人拿掉 1 - 3
块石头。 拿掉最后一块石头的人就是获胜者。 假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石头数量为 n
的情况下赢得游戏。如果可以赢，返回 true；否则，返回 false 。 示例 1： 输入： n = 4 输出：false 解释：如果堆中有
4 块石头，那么你永远不会赢得比赛； 因为无论你拿走 1 块、2 块 还是 3 块石头，最后一块石头总是会被你的朋友拿走。 示例 2：
输入：n = 1 输出：true

这个怎么想，还能怎么想，我是先手吧，那么我只能拿1,2,3,是吧

OK，这里咱们先按照题目的意思去得到一个规律，是啥：
那就是只要石头数量<4 也就是<=3 那么我比依然会赢，直接把石头全部拿走。

OK，然后呢，别急。正常情况下，我们的想法是啥，我先假设我拿一个我看看我会不会赢，然后假设我拿两个，三个。

然后我拿走了一个剩下 n-1 个，此时我再假设对方拿1个，或者2个，3个，在以此类推。也就说如果次数足够多的话你得到的是这样的树结构

就是不知道有没有初中的朋友哈，我没记错的话，是初二学什么排列，概率的时候，有个什么红绿灯的那个问题的吧，然后你画个草图就长这样（我印象比较深刻，我记得我当时好像嘲讽过老师画这个图很呆，然后顶嘴过，然后那啥）

ok，那么这个时候，我其实不用考虑那么多，在递归里面我就考虑一点，当前结构，因为子结构都是一样滴，你看，你考虑你 n 个石头拿走1个，然后另一个人在n-1个石头里面拿走1个的走法是不是类似的，是不是会得到这个上面的树形结构。

显然是滴，那么代码我们就只考虑，当前，然后剩下的让另一个人拿，他输了我就赢了。

public class Nim游戏 {

    public static void main(String[] args) {
        System.out.println(Nim(4));
    }

    public static boolean Nim(int n){
        //正常想法是：先假设自己拿1ok不，然后拿2，然后拿3然后以此类推，然后这里就想到了一个递归结构
        int base = 1;//假设先拿一个

        if(n<4){
            return true;
        }

        while (base<=3){

            if(!Nim(n-base)){
                //剩下的让第二个人去拿
                return true;//输家输了，我就赢了
            }

            base++;
        }

        return false;
    }
}

然后有意思的地方来了。（当然这题你自己找规律其实也能发现）

在多测几个，你会发现规律（这个题目也能直接数学推出来）

class Solution {
    public boolean canWinNim(int n) {
        return n % 4 != 0;
    }
}

然后这个时候，你说搞不到规律，咋办，那简单，知道我为什么要先说回溯不，然后说啥DFS，因为流程是啥

是 先 递归 —》 使用used数组（1/2维）变成DFS（有机会继续就在变成BFS总之是有一个记录的）—》目的是减少递归，甚至变成迭代写法。----》之后想办法看看有没有dp写法，也就是直接记录状态，优化BFS。这里一般用DP是求最优值，所以一般是BFS，当然DFS也有----》然后想办法优化dp。有些题目特征明显就是dp嘛，你就可以直接考虑dp，我这个是指不行的情况下，不行的情况下，只能大力飞砖，咋也没招呀，把分拿上！