大力飞砖之暴力解法(中-上)(DFS与BFS)
文章目录
- 前言
- DFS
-
- 搜索的方向
- 模板
- BFS
-
- 例题
- 模板
前言
前面简单说了一下那个全排列的玩意,那么今天主要是来详细说一说这个DFS和BFS,因为这个还是比较重要的。
DFS
这个玩意呢其实叫做深度优先搜索,首先什么叫深度,说白了就是一撸到底,往里面走,等到碰壁了,然后往回走。那么怎么样实现DFS是最快的(代码写起来最直接)那自然就是直接使用递归嘛。
然后我们直接给出了一个直接递归的代码
public class 跳马 {
//跳跃的步数
static int minStep = Integer.MAX_VALUE;
static int count = 0;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int a = scanner.nextInt();
int b = scanner.nextInt();
int c = scanner.nextInt();
int d = scanner.nextInt();
scanner.close();
BigInteger bigInteger = BigInteger.valueOf(3);
//函数调用
getMin(a,b,c,d);
System.out.println(minStep==Integer.MAX_VALUE?-1:minStep);
}
public static void getMin(int a,int b,int c,int d){
jump(a,b,c,d,0);
}
//jump跳的函数,我们至少是在(1,1)开始的
public static void jump(int a,int b,int c,int d,int step){
if(a<1||a>8||b<1||b>8||c<1||c>8||d<1||d>8){
return;
}
if(a==c&&b==d){
//终止条件
minStep = Math.min(minStep,step);
return;
}
//栈溢出4234!
jump(a+1,b-2,c,d,step+1);
jump(a+2,b-1,c,d,step+1);
jump(a-1,b-2,c,d,step+1);
jump(a-2,b-1,c,d,step+1);
jump(a+2,b+1,c,d,step+1);
jump(a+1,b+2,c,d,step+1);
jump(a-1,b+2,c,d,step+1);
jump(a-2,b+1,c,d,step+1);
jump(a+2,b-1,c,d,step+1);
}
}
然后你发现那啥,你的java堆炸了。
之所以会炸其实很简答,你递归的话,其实会发现有很多路都是走过的,所以我们如果要让代码跑起来最起码,就需要把你的递归次数降低,那么最简单的方式就是记录这个走过的路,那么这个时候我们就需要一个used数组。在很多迷宫问题里面这个used数组其实就是棋盘,我们用这玩意去记录状态。
所以这也是为什么关于棋盘问题的时候需要一个数组表示棋盘,原因其实就是为了记录走过的路。
搜索的方向
在搜索的时候,你可以直接这样例如,上面的 八个方向你可以直接那样写 jump() 写八个,但是实际上呢,我们一般会有个方向数组。
模板
int map[][] //一个记录数组,1/2维度
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
dfs(int x, int y, int step) {
map[x][y] = step;
if (终止条件) {
return;
}
for (int it = 0; it < 4; it++) {
四个方向,或者其他方向去扫描
如果在咱们的那个数组里面记录了,开玩笑,不跑了
if (map[x + dx[it]][y + dy[it]] == 0 && 1 <= x + dx[it] && x + dx[it] <= 4 && 1 <= y + dy[it] && y + dy[it] <= 4) {
dfs(x + dx[it], y + dy[it], step + 1);+
}
}
map[x][y] = 0;
}
这个就是咱们最最基本的架子
后面我们只需要对那个架子做填充就好了。
这个比较简单,没啥好说的。
BFS
BFS 这个呢,其实也不全算是大力飞砖,因为还是使用迭代是吧。所以这个时间复杂度会下来。
那么这个的话也是比较简单的
记住几个步骤
这个的话来个例题吧,DFS的就那个套路,这个BFS 先前说了一个,不过这个下面的题目的话有点小区别,小技巧可以加深你的理解。
例题
import java.util.LinkedList;
import java.util.Queue;
class Node模拟22{
int x;
int y;
public Node模拟22(int x,int y) {
this.x=x;
this.y=y;
}
}
public class 模拟22深度搜索 {
//4000 4000 卡一万
static int[][] used = new int[10010][10010];
//used 记录我们的点
static int[][] direct = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}};
static int centerx = 3000;
static int centery = 3000;
public static void main(String[] args) {
Node模拟22 location1 = new Node模拟22(centerx, centery);
Node模拟22 location2 = new Node模拟22(2020 + centerx, 11 + centery);
Node模拟22 location3 = new Node模拟22(centerx + 11, centery + 14);
Node模拟22 location4 = new Node模拟22(centerx + 2000, centery + 2000);
Queue<Node模拟22> queue = new LinkedList<>();
queue.add(location1);
queue.add(location2);
queue.add(location3);
queue.add(location4);
//开始深度搜索
int j = 0;
//j是分钟
while (j < 2020) {
//当前队列里有多少点 n
int n = queue.size();
for(int xx=0;xx<n;xx++){
//出队
Node模拟22 curLocation = queue.poll();
used[curLocation.x][curLocation.y] = 1;
//然后遍历这个位置的四周可以走通的位置,
for (int i = 0; i < direct.length; i++) {
//如果这个位置的四个周围的节点是可以访问,那么假如队列里面
int x = curLocation.x + direct[i][0];
int y = curLocation.y + direct[i][1];
if (used[x][y] == 1) {
continue;
}
//满足条件 添加到队列里面
//标记当前元素走过
used[x][y] = 1;
//扩散
queue.add(new Node模拟22(x, y));
}
}
j++;
}
int ans = 0;
for (int i = 0; i <= 10000; i++) {
for (int k = 0; k <= 10000; k++) {
if (used[i][k] == 1)
ans++;
}
}
System.out.println(ans);
}
}
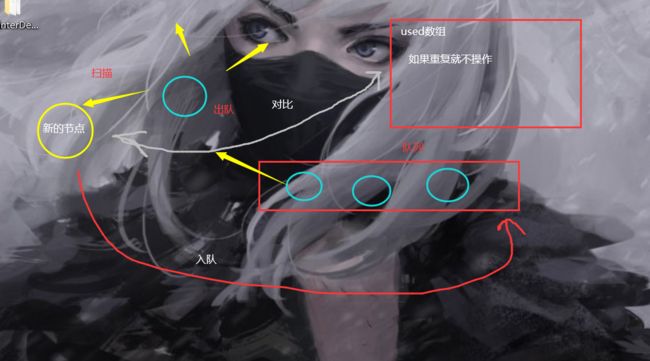
这里的话模板就是我前面的给到图,这个比较特别的是那个,和昨天相比,我们的退出条件不是队列为空,所以我这里给出模板不会那么固定,只会给出这个BFS 需要那些东西,然后去做大致的组合。
模板
一个 used 数组/map
一个队列
初始化队列
出队,让出队的元素扫描,对比used入组(如果你要去重的话)扫描的新节点没有,就再次入队
直到你的终止条件
不过这里的BFS的模板只是一次遍历的模板,如果你还想要拿到那个BFS以后的路径的话,就稍微复杂一点了。遍历一遍BFS简单,拿到过程时间空间复杂度上去了。这里由于时间关系,我就先不说了,比较累今天。
然后关于拿到路径,或者说,你扫描到的状态的这里有两个可以说说,一个是BFS,比如走迷宫,你用BFS走一遍拿到那个路径。还有是dp的背包拿到你拿到的背包有哪些,前面的话是做过有些问题需要拿到前面dp拿到过的状态的,就比如那个种树问题,不过这些套路得看具体情况,我这边总结也只能总结基本的一些东西。