【计算机视觉】局部图像描述子：Harris角点检测及匹配

【计算机视觉】局部图像描述子：Harris角点检测及匹配

1. Harris角点检测器

1.1 检测算法的目标与思想

算法目标：找到角点

算法思想：通过图像局部小窗口观察图像特征，并通过窗口向任意方向移动都会导致图像灰度明显变化的像素窗口内的像素点即为角点。

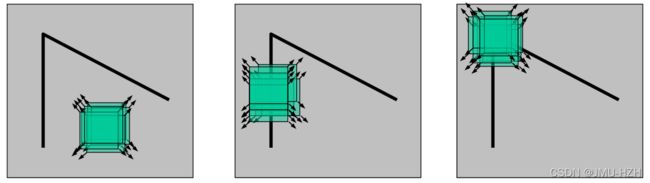
如上图所示，左边的图像在任意方向进行微小的局部平移并不会导致灰度明显的变化，因此可以判断该局部窗口所属区域为平坦区域；中间的图像在上下移动时并不会产生明显的灰度变化，而在左右移动时会产生较大的变化，因此可以判断该局部窗口区域处于一个竖直的边缘；右边的图像在往任意方向进行移动时都会导致图像灰度明显变化，判断局部窗口内的像素点为角点。

1.2 检测算法的数学表达

Harris角点检测思想中很重要的一步是去计算局部窗口滑动前后的像素点灰度变化。因此首先需要了解窗口像素灰度变化的描述表达，如下公式：
$$E(u,v)=\sum _{x,y}w(x,y)[I(x+u,y+v)-I(x,y){]}^2$$

1. [u,v]是窗口的偏移量
2. (x,y)是窗口内的像素坐标(窗口多大，像素多少个)
3. w(x,y)是窗口函数(决定了提取特征的方向，即滤波器)

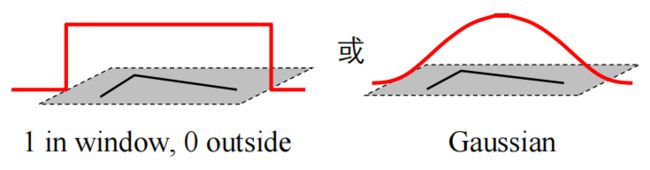
在Harris角点检测中常见的窗口函数采用Gaussian滤波器。滤波器的作用是给像素窗口的每一部分进行加权，采用Gaussian滤波的目的是对于窗口中心点（角点）较近的点进行更多的加权（即认为越近影响越大），较远的点进行更少的加权（即认为越远影响越小）。

在知道像素灰度变化的描述表达后，可以对其进行进一步化简。如下公式，首先将局部移动窗口表达通过泰勒展开进行化简，再将其带入E(u,v)公式进行消参和消除无穷小，获得最后的近似公式。
$$\begin{array}{rl}& I(x+u,y+v)=I(x,y)+I_{x}u+I_{y}v+O\left(u^2,v^2\right)\\ & \\ & E(u,v)=\sum _{x,y}w(x,y){\left[I_{x}u+I_{y}v+O\left(u^2,v^2\right)\right]}^2\\ & \\ & E(u,v)\approx \sum _{x,y}w(x,y){\left[I_{x}u+I_{y}v\right]}^2\end{array}$$
当获得近似公式后将其进行分解代换，最后获得算法中最重要的矩阵M。得到矩阵M，可以发现这个时候求解矩阵的参数就是对于窗口X轴方向的二阶偏导，Y轴方向的二阶偏导和分别对于X轴、Y轴的二阶偏导。
$$\begin{gathered} {\left[I_{x}u+I_{y}v\right]}^2=[u,v]\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\left[\begin{array}{l}u\\ v\end{array}\right] \\ E(u,v)\cong [u,v]M\left[\begin{array}{l}u\\ v\end{array}\right] \\ M=\sum _{x,y}w(x,y)\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right] \end{gathered}$$
通过线性代数的基础知识可以知道，在矩阵的特征值表示矩阵可以进行拉长的程度，而在窗口灰度变化的角度可以理解为灰度强度变化的幅度。这就体现了Harris算法的巧妙之处了，它并没有通过刚刚定义的E(d,u)进行计算，而是通过矩阵M进行窗口任意方向灰度变化的判断。如下图所示，当两个特征值均很大时，说明该点在X轴和Y轴的灰度变化均很大说明该点是角点；若都很小，说明其灰度强度变化很小，为平坦区域；若一大一小则说明其处于边缘。（对应上图1）

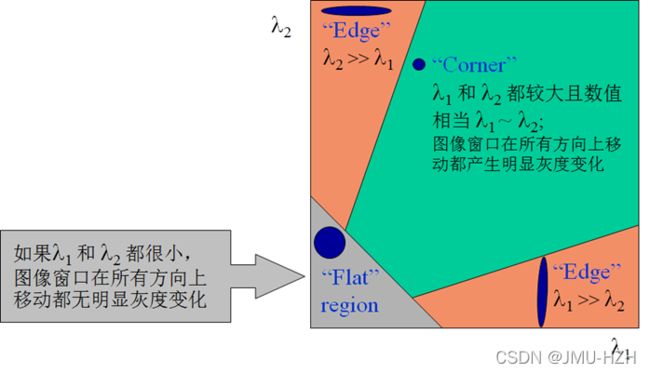
在获得两个方向的特征值后，最后计算响应函数R（响应函数为大数值正数说明该点为角点）。其中特征值的积为矩阵对应行列式的值；特征值的迹为矩阵主对角线之和。
$$\begin{array}{c}R=\frac{\det M}{(\mathrm{trace}M{)}^2}\\ \det M={\lambda }_1{\lambda }_2\\ \mathrm{trace}M={\lambda }_1+{\lambda }_2\end{array}$$

上述图像为获得响应值后的返回图像，红色表示响应值高的像素点。但是如图会发现响应值高的点呈现局部密集现象，这并不是理想状态。因此接下来我们需要通过阈值进行局部极值的提取（接下来的操作将在代码中进行呈现）

1.3 检测算法代码

上述的数学表达中可以看出我们的计算对象是矩阵M，因此代码的第一步是通过高斯滤波对X轴方向和Y轴方向进行一系列的图像导数提取（图像导数可以表示灰度变化）。再进行响应函数的计算。

# 在一幅灰度图像中，对每个函数计算Harris角点检测相应函数
def compute_harris_response(img, sigma = 3):

    # 计算导数
    imx = zeros(img.shape)
    filters.gaussian_filter(img, (sigma,sigma),(0,1), imx)
    
    imy = zeros(img.shape)
    filters.gaussian_filter(img, (sigma,sigma),(1,0), imy)

    # 可视化原图
    plt.subplot(2, 3, 1)
    plt.title('灰度图')
    plt.axis('off')
    plt.imshow(img, plt.cm.gray)

    # 可视化x方向导数图像
    plt.subplot(2, 3, 2)
    plt.title('x方向导数')
    plt.axis('off')
    plt.imshow(imx, plt.cm.gray)

    # 可视化y方向导数图像
    plt.subplot(2, 3, 3)
    plt.title('y方向导数')
    plt.axis('off')
    plt.imshow(imy, plt.cm.gray)

    plt.subplot(2, 3, 4)
    plt.title('x方向二阶导数')
    plt.axis('off')
    plt.imshow(imx * imx, plt.cm.gray)

    plt.subplot(2, 3, 5)
    plt.title('x/y方向二阶导数')
    plt.axis('off')
    plt.imshow(imx * imy, plt.cm.gray)

    plt.subplot(2, 3, 6)
    plt.title('y方向二阶导数')
    plt.axis('off')
    plt.imshow(imy * imy, plt.cm.gray)
    plt.show()

    # 计算Harris矩阵的分量
    Wxx = filters.gaussian_filter(imx*imx,sigma)
    Wxy = filters.gaussian_filter(imx*imy,sigma)
    Wyy = filters.gaussian_filter(imy*imy,sigma)

    # 计算特征值和迹
    
    # 矩阵特征值的积等于行列式的值
    Wdet = Wxx * Wyy - Wxy ** 2

    # 主对角线上元素的和称为矩阵的迹，也是特征值的和
    Wtr = Wxx + Wyy
    return Wdet / Wtr

再获得响应函数后，通过阈值进行角点的局部抑制。并且通过对于图像边缘像素角点的消除以及通过最小距离（找窗口内的极大值）进一步减少角点的冗余。图中的二值化图片是只做了阈值的局部抑制的结果。灰度图是最后提取的结果。

# 从一幅Harris响应图像中返回角点。min_dist为分割角点和图像边界的最少像素数目
def get_harris_points(harrisim, min_dist = 10, threshold = 0.1):

    # 寻找高于阈值的候选角点
    corner_threshold = harrisim.max() * threshold
    #print(corner_threshold)

    harrisim_t = (harrisim > corner_threshold) * 1
    plt.imshow(harrisim_t, plt.cm.gray)
    
    # 得到候选点的坐标(取出是角点的坐标)
    coords = array(harrisim_t.nonzero()).T
    #print(coords.shape)

    # 以及它们的Harris响应值
    candidate_values = [harrisim[c[0],c[1]] for c in coords]

    # 对候选点按照Harris响应值进行排序
    index = argsort(candidate_values)

    # 将可行点的位置保存到数组中
    allowed_location = zeros(harrisim.shape)
    # 相当于把外面一圈有响应值的点先舍去（匹配主体在中心）
    allowed_location[min_dist:-min_dist, min_dist:-min_dist] = 1

    # 按照min_distance原则，选择最佳的Harris角点
    filtered_coords = []
    for i in index:
        if allowed_location[coords[i,0],coords[i,1]] == 1:
            filtered_coords.append(coords[i])
            allowed_location[(coords[i,0] - min_dist):(coords[i,0] + min_dist), (coords[i,1] - min_dist):(coords[i,1] + min_dist)] = 0
    
    return filtered_coords

# 绘制图像中检测到的角点
def plot_harris_point(image, filtered_coords):
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords],[p[0] for p in filtered_coords],'*')
    axis('off')
    show()
    
if "__main__" == __name__:
    # 打开灰度图convert('L')
    img = array(Image.open("harris/test1.jpg").convert('L'))

    harrisim = compute_harris_response(img)

    # harrisim1 = 255 - harrisim
    # img1 = Image.fromarray(harrisim1)
    # figure()
    # gray()
    # imshow(img1)
    # show()

    filtered_coords = get_harris_points(harrisim,6)
    plot_harris_point(img, filtered_coords)

2. Harris角点匹配

2.1 角点匹配过程

角点匹配步骤：
1. 将检测出来的角点进行特征描述
2. 将匹配的两张图片的所有角点特征描述通过归一化互相关获得匹配的得分
3. 通过两张图片互相的匹配（两个版本：1->2,2->1）进行匹配点的筛选

2.2 角点特征描述

Harris角点的特征描述很直观，就是角点周围像素块的灰度值。具体来说就是以角点为中心划出来的一个patch。

# 获得角点的特征描述（划分以角点为中心的5*5区域）
def get_descriptors(image, filtered_coords, wid = 5):
    desc = []
    for coords in filtered_coords:
        patch = image[coords[0] - wid:coords[0] + wid + 1, coords[1] - wid:coords[1] + wid + 1].flatten()
        desc.append(patch)
    return desc

2.3 归一化互相关

如上述代码可得，每张图片都会产生若干个特征描述（几个角点几个特征描述)，将两幅图像的特征描述进行**穷举比对（一张图片中的每一个角点特征描述都分别与另一张图片中的所有角点特征描述进行匹配）**最后获得一系列的匹配得分，再通过阈值进行筛选，最后获得匹配结果。

而获得匹配得分的方式是通过归一化互相关，公式如下：
$$ncc\left({\mathbf{I}}_1,{\mathbf{I}}_2\right)=\frac{1}{n-1}\sum _{\mathbf{x}}\frac{\left({\mathbf{I}}_1(\mathbf{x})-{\mu }_1\right)}{{\sigma }_1}\cdot \frac{\left({\mathbf{I}}_2(\mathbf{x})-{\mu }_2\right)}{{\sigma }_2}$$

# 归一化互相关获得得分
def match(desc1, desc2, threshold = 0.5):
    n = len(desc1[0])
    d = -ones((len(desc1),len(desc2)))
    for i in tqdm(range(len(desc1))):
        for j in range(len(desc2)):
            d1 = (desc1[i] - mean(desc1[i])) / std(desc1[i])
            d2 = (desc2[j] - mean(desc2[j])) / std(desc2[j])
            ncc_value = sum(d1 * d2) / (n-1)
            if ncc_value > threshold:
                d[i,j] = ncc_value

    ndx = argsort(-d)
    matchscores = ndx[:,0]
    return matchscores

# 进行两边对称版本的匹配
def match_twosided(desc1, desc2, threshold = 0.5):
    matches_12 = match(desc1,desc2,threshold)
    matches_21 = match(desc2,desc1,threshold)

    ndx_12 = where(matches_12 >= 0)[0]

    # 筛去不匹配的点
    for n in ndx_12:
        if matches_21[matches_12[n]] != n:
            matches_12[n] = -1
    
    return matches_12

def appendimages(img1,img2):
    rows1 = img1.shape[0]
    rows2 = img2.shape[0]

    if rows1 < rows2:
        img1 = concatenate((img1, zeros((rows2 - rows1, img1.shape[1]))),axis = 0)
    elif rows1 > rows2:
        img2 = concatenate((img2, zeros((rows1 - rows2, img2.shape[1]))),axis = 0)

    return concatenate((img1,img2), axis = 1)

def plot_matches(img1, img2, locs1, locs2, matchscores, show_below = False):
    img3 = appendimages(img1, img2)
    if show_below:
        img3 = vstack((img3,img3))

    imshow(img3)

    cols1 = img1.shape[1]
    for i,m in enumerate(matchscores):
        if m > 0:
            plot([locs1[i][1],locs2[m][1] + cols1],[locs1[i][0],locs2[m][0]],'c')
    axis('off')
    
if "__main__" == __name__:
    # 打开灰度图convert('L')
    img1 = array(Image.open("harris/test1.jpg").convert('L'))
    img2 = array(Image.open("harris/test2.jpg").convert('L'))

    wid = 5 
    harrisim = compute_harris_response(img1,5)
    filtered_coords1 = get_harris_points(harrisim, wid + 1)
    d1 = get_descriptors(img1,filtered_coords1,wid)

    harrisim = compute_harris_response(img2,5)
    filtered_coords2 = get_harris_points(harrisim, wid + 1)
    d2 = get_descriptors(img2,filtered_coords2,wid)

    print("starting matching")
    matches = match_twosided(d1,d2)

    figure()
    gray()
    plot_matches(img1,img2,filtered_coords1,filtered_coords2,matches)
    show()

2.4 匹配结果可视化