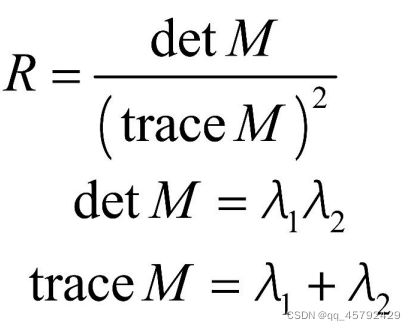qq_45792429

计算机视觉（二）：局部图像描述子

计算机视觉二：局部图像描述子

一、序
- 1、角点（corner points）
- 2. 如何判断是否是好的角点检测算法
二、Harris角点检测器
- 1、基本思想
- 2、数学表达
- 3、角点计算流程
- 4、算法实现
- - 4.1 角点响应函数
  - 4.2 筛选角点
  - 4.3 显示角点
  - 4.4 结果显示
- 5. 寻找对应点
- - 5.1 兴趣点描述子
  - - 5.1.1 获取图像像素块，并使用归一化的互相关矩阵进行比较
    - 结果显示
三、SIFT算法
- 1、产生
- 2、了解
- - 2.1 兴趣点
  - 2.2 描述子
  - 2.3 检测兴趣点
  - 2.4 匹配描述子
四、匹配地理标记图像
- 1、下载地理标记图像
- 2、使用局部描述子匹配
- 3、可视化连接的图像

一、序

局部图像描述子主要是为了寻找图像间的对应点和对应区域。以下内容将出现两种用于图像匹配的局部描述子算法。
特征匹配的基本流程：

根据特定准则，提取图像中的特征点
提取特征点周围的图像块，构造特征描述符
通过特征描述符对比，实现特征匹配
特征点必须具有不变性

特征可以分为以下几类：

角点：Harris算子，SUSAN算子。FSAT算子
梯度特征点：SIFT、SURF、GLOH、ASIFT、PSIFT算子
边缘特征（线性）：Canny算子、Marr算子
纹理特征：灰度共生矩阵，小波Gabor算子
快速特征匹配的基本策略：以图像中稳定角点的领域训练特征分类器，为输入图像的特征分类

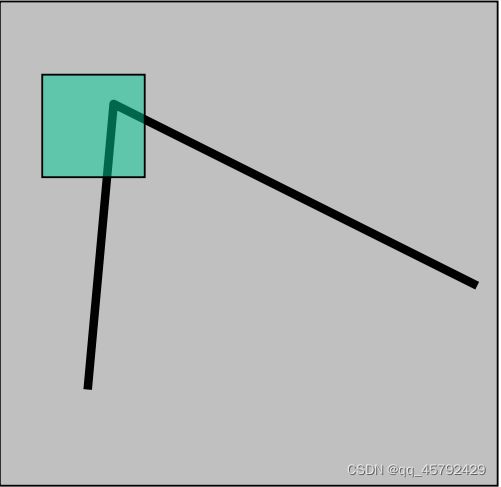
1、角点（corner points）

局部窗口沿各方向移动，均产生明显变化的点
图像局部曲率突变的点

经典的角点检测算法
Harris角点检测
CSS角点检测

2. 如何判断是否是好的角点检测算法

检测出图像中“真实的”角点
准确的定位性能
很高的稳定性
具有对噪声的鲁棒性
具有较高的计算效率

二、Harris角点检测器

1、基本思想

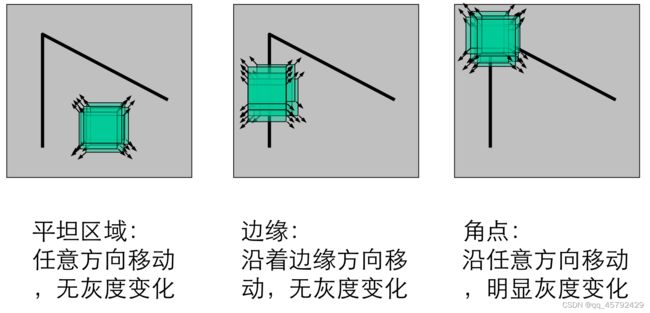
从图像局部的小窗口观察图像特征，利用角点定义判断，如下图

如果在平坦区域：那么超任意方向移动，都无灰度变化
如果在边缘处移动：沿着边缘方向移动，无灰度变化
在角点处：沿任意方向移动，有明显的灰度变化

2、数学表达

将图像窗口平移==[u,v]产生灰度变化E(u,v)==

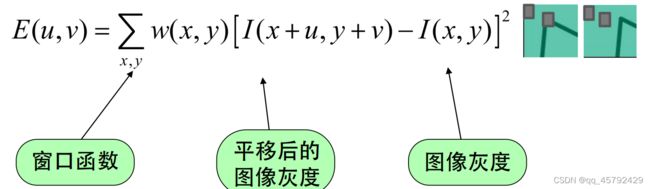
我们可以利用泰勒展开来获得上图式子中的E和I
窗口函数的两种表示：

对于局部微小的移动量[u,v]，我们可以获得以下近似值

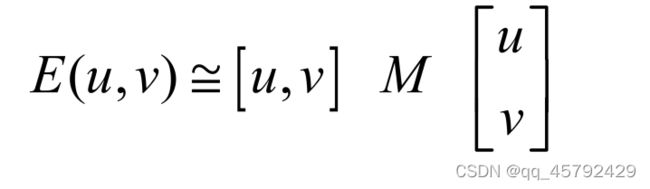
M是由图像的导数求得的2X2的矩阵。
所以窗口移动导致的图像变化量其实就是对对称矩阵M的特征值分析，通过两个特征值的大小我们可以对图像点进行分类：

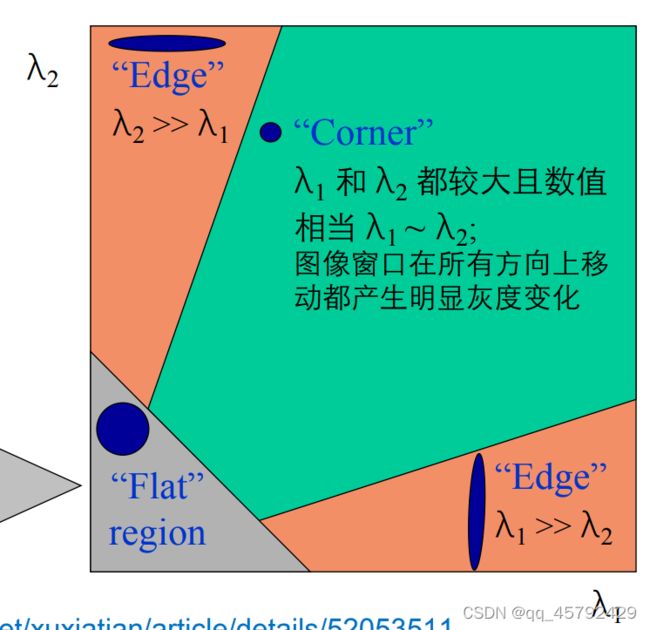
当两个特征值都很小时，图像窗口在所有方向上移动都无明显灰度变化
我们可以定义一个角点响应函数R：

我们将上面的区域划分换一种划分方式，则为：

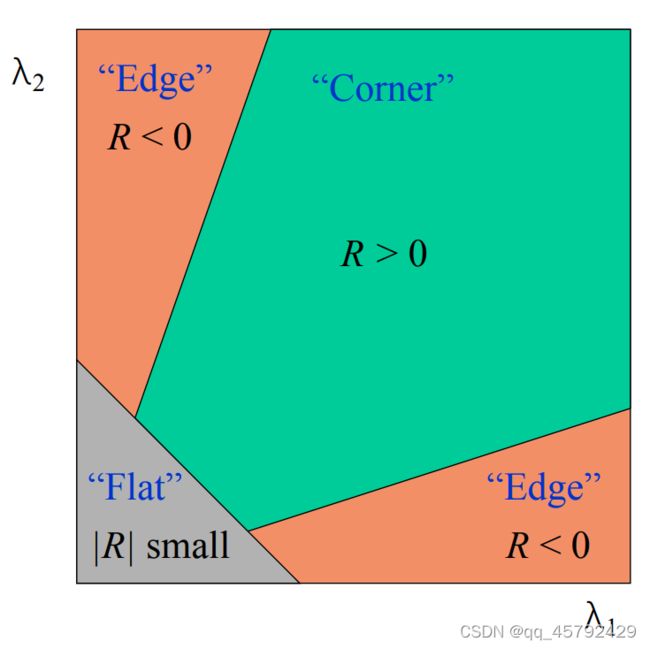
我们可以看到：
在角点时：R为大叔之正数
在边缘点时：R为大数值负数
在平坦区时：R为小数值

3、角点计算流程

对角点响应函数R进行阈值处理
R>threshold
提取R的局部极大值

为了消除参数k的影响，也可以采用商来计算响应：

4、算法实现

4.1 角点响应函数

from scipy.ndimage import filters


def compute_harris_response(im,sigma=3):
    """ Compute the Harris corner detector response function 
        for each pixel in a graylevel image. """
    
    
    imx = zeros(im.shape)
    filters.gaussian_filter(im, (sigma,sigma), (0,1), imx)
    imy = zeros(im.shape)
    filters.gaussian_filter(im, (sigma,sigma), (1,0), imy)
    
    Wxx = filters.gaussian_filter(imx*imx,sigma)
    Wxy = filters.gaussian_filter(imx*imy,sigma)
    Wyy = filters.gaussian_filter(imy*imy,sigma)
    
    Wdet = Wxx*Wyy - Wxy**2
    Wtr = Wxx + Wyy
    
    return Wdet / (Wtr*Wtr)

4.2 筛选角点

def get_harris_points(harrisim,min_dist=10,threshold=0.1):
    
    # find top corner candidates above a threshold
    corner_threshold = harrisim.max() * threshold
    harrisim_t = (harrisim > corner_threshold) * 1
    
    # get coordinates of candidates
    coords = array(harrisim_t.nonzero()).T
    
    # ...and their values
    candidate_values = [harrisim[c[0],c[1]] for c in coords]
    
    # sort candidates
    index = argsort(candidate_values)
    
    # store allowed point locations in array
    allowed_locations = zeros(harrisim.shape)
    allowed_locations[min_dist:-min_dist,min_dist:-min_dist] = 1
    
    # select the best points taking min_distance into account
    filtered_coords = []
    for i in index:
        if allowed_locations[coords[i,0],coords[i,1]] == 1:
            filtered_coords.append(coords[i])
            allowed_locations[(coords[i,0]-min_dist):(coords[i,0]+min_dist), 
                        (coords[i,1]-min_dist):(coords[i,1]+min_dist)] = 0
    
    return filtered_coords

4.3 显示角点

def plot_harris_points(image,filtered_coords):
    
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords],
                [p[0] for p in filtered_coords],'*')
    axis('off')
    show()

4.4 结果显示

原图：

5. 寻找对应点

5.1 兴趣点描述子

分配给兴趣点的一个向量，描述该点附近的图像的表观信息。描述子约到，寻找到的对应点越好。描述子通常是由周围图像像素块的灰度值，以及用于比较归一互相关矩阵构成的。

5.1.1 获取图像像素块，并使用归一化的互相关矩阵进行比较

def get_descriptors(image,filtered_coords,wid=5):
    
    desc = []
    for coords in filtered_coords:
        patch = image[coords[0]-wid:coords[0]+wid+1,
                            coords[1]-wid:coords[1]+wid+1].flatten()
        desc.append(patch)
    
    return desc

def match(desc1,desc2,threshold=0.5):
    
    n = len(desc1[0])
    
    # pair-wise distances
    d = -ones((len(desc1),len(desc2)))
    for i in range(len(desc1)):
        for j in range(len(desc2)):
            d1 = (desc1[i] - mean(desc1[i])) / std(desc1[i])
            d2 = (desc2[j] - mean(desc2[j])) / std(desc2[j])
            ncc_value = sum(d1 * d2) / (n-1) 
            if ncc_value > threshold:
                d[i,j] = ncc_value
            
    ndx = argsort(-d)
    matchscores = ndx[:,0]
    
    return matchscores

def match_twosided(desc1,desc2,threshold=0.5):
    
    matches_12 = match(desc1,desc2,threshold)
    matches_21 = match(desc2,desc1,threshold)
    
    ndx_12 = where(matches_12 >= 0)[0]
    
    # remove matches that are not symmetric
    for n in ndx_12:
        if matches_21[matches_12[n]] != n:
            matches_12[n] = -1
    
    return matches_12

匹配点可视化

def appendimages(im1,im2):
    
    # select the image with the fewest rows and fill in enough empty rows
    rows1 = im1.shape[0]    
    rows2 = im2.shape[0]
    
    if rows1 < rows2:
        im1 = concatenate((im1,zeros((rows2-rows1,im1.shape[1]))),axis=0)
    elif rows1 > rows2:
        im2 = concatenate((im2,zeros((rows1-rows2,im2.shape[1]))),axis=0)
    # if none of these cases they are equal, no filling needed.
    
    return concatenate((im1,im2), axis=1)
def plot_matches(im1,im2,locs1,locs2,matchscores,show_below=True):
    
    im3 = appendimages(im1,im2)
    if show_below:
        im3 = vstack((im3,im3))
    
    imshow(im3)
    
    cols1 = im1.shape[1]
    for i,m in enumerate(matchscores):
        if m>0:
            plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
    axis('off')

结果显示

三、SIFT算法

1、产生

David G.Lowe教授总结了基于特征不变技术的检测方法，在图像尺度空间基础上，提出对图像缩放、旋转保存不变性的图像局部特征描述算子–SIFT，即尺度不变特征变换。
SIFT算法可以解决以下问题：

目标的旋转、缩放、平移
图像仿射/投影变换
弱光照影响
部分目标遮挡
杂物场景
噪声

2、了解

实质可以归为在不同尺度空间商查找特征点（关键点）的问题

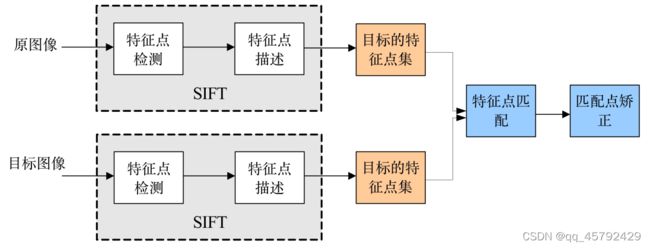
流程如下：

提取关键点
对关键点附加详细信息（局部特征），即描述符
通过特征点（附带上特征向量的关键点）的两两比较找出相互匹配的若干对特征点，建立对应关系

SIFT要查找的点是一些十分突出的点，不会因光照、尺度、旋转等因素的改变而消失，比如：角点、边缘点、暗区域的点以及亮区域的暗点。也就是说SIFT希望选出在尺度、旋转、亮度都具有不变性的点

主要思想是通过对原始图像进行尺度变换，获得图像多尺度下的空间表示。从而实现边缘、角点检测和不同分辨率上的特征提取，以满足特征点的尺度不变性。尺度越大图像越模糊。

2.1 兴趣点

SIFT特征使用高斯差分函数来定位兴趣点：

DoG高斯差分金字塔：对应DOG算子，需构建DOG金字塔
通过高斯差分图像看出图像上的像素值变化情况。如果没有变化，也就没有特征。特征必须是变化尽可能多的点。DOG图像描绘的是目标轮廓。

DOG的局部极值点：特征点是由DOG空间得局部极值点组成的。每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。

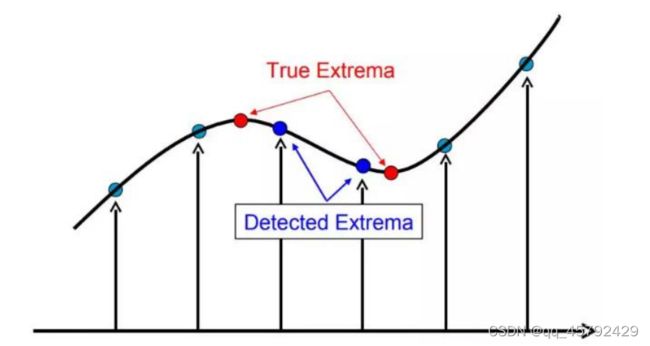
中间的监测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

去除边缘响应DOG函数在图像边缘有较强的边缘响应。DOG函数的峰值点在边缘方向有较大的主曲率，在垂直边缘的方向有较小的主曲率。主曲率可以通过计算在该点位置尺度的2×2的Hessian矩阵得到。

2.2 描述子

为了实现旋转不变性，基于每个点周围图像梯度的方向和大小。SIFT描述子又引入参考方向。SIFT描述子使用主方向描述参考方向。

2.3 检测兴趣点

使用开源工具包VLFeat提供的二进制文件来计算图像的SIFT特征。代码如下：

def process_image(imagename,resultname,params="--edge-thresh 10 --peak-thresh 5"):

    if imagename[-3:] != 'pgm':
        # create a pgm file
        im = Image.open(imagename).convert('L')
        im.save('tmp.pgm')
        imagename = 'tmp.pgm'

    cmmd = str("sift "+imagename+" --output="+resultname+
                " "+params)
    os.system(cmmd)
    print ('processed', imagename, 'to', resultname)
    
#读取特征数值到数值
def read_features_from_file(filename):
    
    f = loadtxt(filename)
    return f[:,:4],f[:,4:]

#输出结构保存到特征图片
def write_features_to_file(filename,locs,desc):
    savetxt(filename,hstack((locs,desc)))


#可视化
def plot_features(im,locs,circle=False):

    def draw_circle(c,r):
        t = arange(0,1.01,.01)*2*pi
        x = r*cos(t) + c[0]
        y = r*sin(t) + c[1]
        plot(x,y,'b',linewidth=2)

    imshow(im)
    if circle:
        for p in locs:
            draw_circle(p[:2],p[2]) 
    else:
        plot(locs[:,0],locs[:,1],'ob')
    axis('off')

结果显示：
待续。。。

2.4 匹配描述子

一图像中的特征匹配到另一幅图像的特征，使用两个特征距离和两个最匹配特征距离的比率。相对于图像的其他特征，该准则保证能够找到足够相似的唯一特征。能够降低错误的匹配数。

代码：

def match(desc1,desc2):
    
    desc1 = array([d/linalg.norm(d) for d in desc1])
    desc2 = array([d/linalg.norm(d) for d in desc2])
    
    dist_ratio = 0.6
    desc1_size = desc1.shape
    
    matchscores = zeros((desc1_size[0]),'int')
    desc2t = desc2.T # precompute matrix transpose
    for i in range(desc1_size[0]):
        dotprods = dot(desc1[i,:],desc2t) # vector of dot products
        dotprods = 0.9999*dotprods
        # inverse cosine and sort, return index for features in second image
        indx = argsort(arccos(dotprods))
        
        # check if nearest neighbor has angle less than dist_ratio times 2nd
        if arccos(dotprods)[indx[0]] < dist_ratio * arccos(dotprods)[indx[1]]:
            matchscores[i] = int(indx[0])
    
    return matchscores

该函数使用描述子向量间的家教作为距离度量。但是我们需要将描述子向量归一化到单位长度。因为匹配是单向的，所以我们可以先计算第二幅图兴趣点描述子向量的装置矩阵。

为了增加匹配的稳健性，我们可以再反过来执行一次该步骤，从第二幅图象中的特征向第一幅图像中的特征匹配。最后，我们保留同时满足这两种匹配准则的对应。代码如下：

def match_twosided(desc1,desc2):
    
    matches_12 = match(desc1,desc2)
    matches_21 = match(desc2,desc1)
    
    ndx_12 = matches_12.nonzero()[0]
    
    # remove matches that are not symmetric
    for n in ndx_12:
        if matches_21[int(matches_12[n])] != n:
            matches_12[n] = 0
    
    return matches_12