数据结构与算法python语言实现 Michael T.Goodrich- Chapter3&Chapter4课后习题

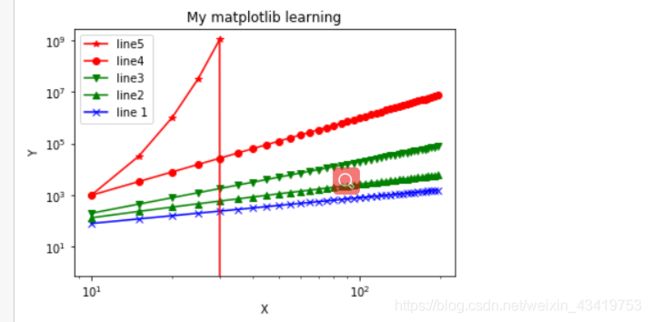
R3.1以log为坐标画出函数4n、4nlogn、2n³、n³、2ⁿ四个图形

import numpy as np
import matplotlib.pyplot as plt
import math
a = plt.subplot(1,1,1)
x = np.arange(10,200,5)
y2 =[4*m*math.log(m,2)for m in x]

#这里b表示blue，g表示green，r表示red，-表示连接线，--表示虚线链接
a1 = a.plot(x, 8*x, 'bx-', label = 'line 1')
a2 = a.plot(x,  y2, 'g^-', label = 'line2')
a3 = a.plot(x, 2*x**2, 'gv-', label = 'line3')
a4 = a.plot(x, x**3, 'ro-', label = 'line4')
a5 = a.plot(x, 2**x, 'p
*-', label = 'line5')

#标记图的题目，x和y轴
plt.title("My matplotlib learning")
plt.xlabel("X")

plt.ylabel("Y")


#显示图例
handles, labels = a.get_legend_handles_labels()
a.legend(handles[::-1], labels[::-1])
#转换成对数坐标
plt.semilogx(2)
plt.semilogy(2)
plt.show()

运行结果：

R-4.1 递归算法找出序列最大值，并给出算法的时间和空间复杂度

def sum_recursive(list):
    if len(list)==1:
        return list[0]
    return list[0] if list[0]>sum_recursive(list[1:]) else sum_recursive(list[1:])

sum_recursive([1,38,2,90])
90

算法时间复杂度O[n],空间复杂度O[n]

R-4.6计算第n个调和数

def harmonic_number(n):
    if n == 1:
        return 1
    else:
        return 1/n + harmonic_number(n-1)

harmonic_number(4)
2.083333333333333

R-4.7 将一串数字转换成整数

#R-4.7
INT_MIN = -2147483648
INT_MAX = 2147483647
def convert(s):
        """
        :type str: str
        :rtype: int
        """
        if len(s) is 0:
            return 0
        c = s[0]
        if c in ' ':
            # greedily eat space
            return self.convert(s[1:])
        
        depth = 0
        def incrementDepth():
            # in languages with a ++ operator this is unnecessary
            # because a++ evaluates to a (and increments a)
            nonlocal depth
            depth += 1
            return 0
        def inner(s):
            nonlocal depth
            if len(s) is 0:
                return 0
            c = s[0]
            if c not in "0123456789":
                return 0
            # this is the magic; we need to evaluate depth AFTER
            # recursing and BEFORE incrementing it
            return inner(s[1:]) + 10**(depth) * (ord(c) - 48) + incrementDepth()
        
        # non greedily eat other leading chars
        if c in "-":
            return max(-1 * inner(s[1:]), INT_MIN)
        if c in "+":
            return min(inner(s[1:]), INT_MAX)
        return min(max(inner(s), INT_MIN), INT_MAX)

s = '12123'
convert(s)
12123

C-4.9用简短的递归python函数，在不使用循环的条件下查找一个序列的最小值和最大值

def getMaxMin(nums,low,high):
    if low>= high:
        return nums[low],nums[high]
    mid = (low+high)//2
    leftmax,leftmin=getMaxMin(nums,low,mid)
    rightmax,rightmin=getMaxMin(nums,mid+1,high)
    if leftmax<rightmax:
        leftmax=rightmax
    if leftmin>rightmin:
        leftmin=rightmin

    return [leftmax,leftmin]

nums = [10,223,18,890,23,12,142]
low =0
high = len(nums)-1
getMaxMin(nums,low,high)(nums,low,high)

输出：(890，10)

C-4.10 用递归算法计算以2为底的n的对数的整数部分

def log2(a,n = 0):
    if a >=1:
        if a >= 1 and a< 2:
            return n
        return log2(a/2,n+1)
    else:
        if a>= 1/2 and a<1:
            return n-1
    return log2(a*2,n-1)

log2(5)
2

c.14汉诺塔问题

def move(n,a,b,c):
    if n == 1: 
        print(a,"--->",c)
    else:
        move(n-1,a,c,b)
        print(a,"--->",c)
        move(n-1,b,a,c)

move(4,'a','b','c')
a ---> b
a ---> c
b ---> c
a ---> b
c ---> a
c ---> b
a ---> b
a ---> c
b ---> c
b ---> a
c ---> a
b ---> c
a ---> b
a ---> c
b ---> c

C-4.16输出字符串的逆序以及判断是否是一个回文

def reverse(s,start,stop):
    
    if start < stop -1:
        s[start],s[stop-1] = s[stop-1],s[start]
        reverse(s,start+1,stop-1)
        return ''.join(s)

s = 'asdguasdga'
s = list(s)
start = 0
stop = len(s)
print(reverse(s,start,stop))
s == reverse(s,start,stop)

'agdsaugdsa'
False

C-4.19输出序列偶数值在奇数值前面

def chapter4_func19(arr,start,stop):
    if stop -start <1:
        return arr
    if stop - start >= 1:
        if arr[start] %2 ==0 and arr[stop] %2 ==0:
            return chapter4_func19(arr,start+1,stop)
        if arr[start] %2 == 1 and arr[stop] %2 == 1:
            return chapter4_func19(arr,start,stop-1)
        if arr[start] %2 == 1 and arr[stop]%2 ==0:
            arr[start],arr[stop] = arr[stop],arr[start]
            return chapter4_func19(arr,start+1,stop-1)
        if arr[start] %2 == 0 and arr[stop] %2 == 1:
            return chapter4_func19(arr,start +1 ,stop -1)

arr = [1,2,32,5,24,23,423]
start = 0
stop = len(arr) -1
chapter4_func19(arr,start,stop)


[24, 2, 32, 5, 1, 23, 423]

c-4.21用递归算法找到序列S 中总和为k的两个整数，找到输出True、否则False

def chapter4_func21(arr,start,stop,k):
    if stop- start <1:
        return arr[start] + arr[stop] == k
           
    
    if stop -start >= 1:
        if arr[stop] + arr[start] == k:
            return True
        
        if arr[start] + arr[stop] > k:
            return chapter4_func21(arr,start,stop-1,k)
        if  arr[start] + arr[stop] <k:
            return chapter4_func21(arr,start+1,stop,k)

arr = [1,3,5,6,7,120,123]
start = 0
stop = len(arr) -1
k = 178
chapter4_func21(arr,start,stop,k)

False