NumPy学习笔记(1)- NumPy基础
NumPy应用场景
- 与SciPy(Scientific Python)和Matplotlib一起使用,可代替Matlab
- SciPy:开源Python算法库和数学工具包,包含最优化、线性代数、积分、插值、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算模块。
- Matplotlib:利用通用的图形用户界面工具包,如 Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口(API)
NumPy比python原生数组计算更高效的原因
- 内存:NumPy在内存空间中连续存储数据,而python列表每个元素是分散的
- 向量化运算:NumPy内置了并行运算功能
- 底层代码:NumPy底层用C编写,内部解除了GIL(全局解释锁)
目录
文章目录
- 1-NumPy对象和数据类型
-
- 1-1 Ndarray对象
-
- Ndarray构成
- 对象创建
-
- 实例
- 1-2 数据类型
-
- dtype对象
-
- 构造dtype对象
- 实例1
- 实例2
- 内建类型
- 1-3 ndarray属性
- 1-4 创建数组
-
- ndarray构造器
- 其他方式
-
- numpy.empty
- numpy.zeros
- numpy.ones
- 从已有数组创建
-
- numpy.asarray
- numpy.frombuffer
- numpy.fromiter
- 从数值范围创建
-
- numpy.arange
- numpy.linspace
- numpy.logspace
- 1-5 NumPy切片和索引
-
- 基本索引方式
-
- n≥3维度数组的索引
- 高级索引
-
- 整数数组索引
- 布尔索引
- 花式索引
- 2 - NumPy运算
-
- 2-1 Broadcast
- 2-2 迭代数组
-
- 迭代访问顺序
-
- 默认访问顺序
- 指定访问顺序
- 修改数组中元素的值
- 使用外部循环
- 广播迭代
- 2-3 数组运算
-
- NumPy数组操作
-
- 修改数组形状
- 翻转数组
- 修改数组维度
- 连接数组
- 分割数组
- 数组元素的添加与删除
- 2-4 位运算
- 3 - 常用函数
-
- 3-1 字符串函数
- 3-2 数学函数
-
- 三角函数
- 指数和对数
- 3-3 算术函数
- 3-4 统计函数
- 专用的通用函数
- 3-5 排序、条件筛选函数
-
- numpy.sort()
- numpy.lexsort()
- np.msort(a)
- sort_complex(a)
- partition(a, kth[, axis, kind, order])
- index functions
-
- numpy.argmax()和numpy.argmin()
- numpy.argsort()
- argpartition(a, kth[, axis, kind, order])
- numpy.nonzero()
- numpy.where()
- numpy.extract()
- 4 - 扩展
-
- 4-1 字节交换
- 4-2 副本和视图
-
- 赋值
- 视图/浅拷贝
- 副本/深拷贝
- 4-3 矩阵库
-
- 转置矩阵
- matlib.empty()
- matlib.zeros()
- matlib.ones()
- matlib.eye()
- matlib.identity()
- 4-4 线性代数
-
- numpy.dot()
- numpy.vdot()
- numpy.inner()
- numpy.matmul()
- numpy.linalg.det()
- numpy.linalg.solve()
- numpy.linalg.inv()
- 4-5 IO
-
- numpy.save()
- numpy.savez()
- savetxt()
- 4-6 Matplotlib
-
- 基本操作
- 字体设置
-
- 使用官方字体
- 自定义字体文件
- 绘制散点图
- 绘制正弦图
- plt.subplot
- 将图形绘制在同一区域
- plt.bar()
- numpy.histogram()与直方图
1-NumPy对象和数据类型
1-1 Ndarray对象
NumPy 最重要的一个特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
Ndarray构成
ndarray 内部由以下内容组成
- 一个指向数据(内存或内存映射文件中的一块数据)的指针。
- 数据类型或 dtype,描述在数组中的固定大小值的格子。
- 一个表示数组形状(shape)的元组,表示各维度大小的元组。
- 一个跨度元组(stride),其中的整数指的是为了前进到当前维度下一个元素需要"跨过"的字节数。
对象创建
numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)
- object:数组或嵌套的数列
- dtype:数据类型,可选
- copy:对象是否需要复制,可选
- order:创建数组的样式,C为行方向,F为列方向,A为任意方向(默认)
- subok:默认返回一个与基类类型一致的数组
- ndmin:指定生成数组的最小维度
实例
import numpy as np
a = np.array([1,2,3])
print('a:\n',a,'\n')
#多于一个维度
b = np.array([[1,2],[3,4]])
print('b:\n',b,'\n')
#最小维度
c = np.array([1,2,3,4,5], ndmin = 2)
print('c:\n',c,'\n')
# dtype参数
d = np.array([1,2,3], dtype = complex)
print('d:\n',d)
输出结果:
a:
[1 2 3]
b:
[[1 2]
[3 4]]
c:
[[1 2 3 4 5]]
d:
[1.+0.j 2.+0.j 3.+0.j]
1-2 数据类型
numpy的数值类型是dtype对象的实例,并对应唯一的字符,包括np.bool_, np.int32, np.float32等。
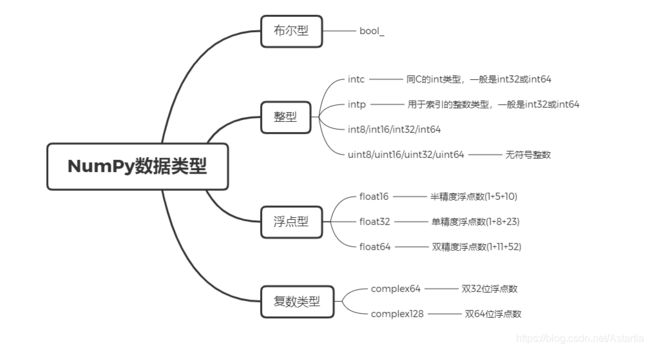
dtype对象
数据类型对象(numpy.dtype 类的实例)用来描述与数组对应的内存区域是如何使用,它描述了数据的以下几个方面:
- 数据的类型(整数,浮点数或者 Python 对象)
- 数据的大小(例如, 整数使用多少个字节存储)
- 数据的字节顺序(小端法或大端法)在结构化类型的情况下,字段的名称、每个字段的数据类型和每个字段所取的内存块的部分
- 如果数据类型是子数组,那么它的形状和数据类型是什么。
字节顺序是通过对数据类型预先设定 < 或 > 来决定的。 < 意味着小端法(最小值存储在最小的地址,即低位组放在最前面)。> 意味着大端法(最重要的字节存储在最小的地址,即高位组放在最前面)
构造dtype对象
numpy.dtype(object, align, copy)
- object - 要转换为的数据类型对象
- align - 如果为true,填充字段使其类似C的结构体
- copy - 复制dtype对象,如果为false,则是对内置数据类型对象的引用
实例1
import numpy as np
# 创建结构化数据类型
dt = np.dtype([('age', np.int8)])
print(dt)
# 将数据类型应用于ndarray对象
a = np.array([(10,),(20,),(30,)], dtype = dt)
print(a)
# 类型字段名可以用于存取实际的age列
print(a['age'])
输出结果:
[('age', 'i1')]
[(10,) (20,) (30,)]
[10 20 30]
实例2
import numpy as np
student = np.dtype([('name','S20'),('age','i1'),('marks','f4')])
print(student)
a = np.array([('Jack',21,98),('Rose',19,100),('@lbert',25,150)], dtype = student)
print(a)
输出结果:
[('name', 'S20'), ('age', 'i1'), ('marks', ')]
[(b'Jack', 21, 98.) (b'Rose', 19, 100.) (b'@lbert', 25, 150.)]
内建类型
| 字符 | 对应类型 |
|---|---|
| b | boolean |
| i | integer |
| u | 无符号整型 |
| f | float |
| c | complex |
| m | timedelta |
| M | datetime |
| O | (python)object |
| S,a | (byte-)字符串 |
| U | Unicode |
| V | 原始数据void |
1-3 ndarray属性
NumPy 数组的维数称为秩(rank),每一个线性的数组称为是一个轴(axis),也就是维度(dimensions)。
比如说,二维数组相当于是两个一维数组,其中第一个一维数组中每个元素又是一个一维数组。所以一维数组就是 NumPy 中的轴(axis),第一个轴相当于是底层数组,第二个轴是底层数组里的数组。而轴的数量——秩,就是数组的维数。很多时候可以声明 axis。axis=0,表示沿着第 0 轴进行操作,即对每一列进行操作;axis=1,表示沿着第1轴进行操作,即对每一行进行操作。
| attribute | description |
|---|---|
| ndarray.ndim | 秩,即轴的数量或维度的数量 |
| ndarray.shape | 数组的维度 |
| ndarray.size | 数组元素的总个数 |
| ndarray.dtype | ndarray对象的元素类型 |
| ndarray.itemsize | ndarray对象中每个元素的大小,以字节为单位 |
| ndarray.flags | ndarray对象的内存信息 |
| ndarray.real | ndarray元素的实部 |
| ndarray.imag | ndarray元素的虚部 |
| ndarray.data | 包含实际数组元素的缓冲区 |
1-4 创建数组
ndarray构造器
- 见1.1
其他方式
numpy.empty
- 创建一个指定形状、数据类型且未初始化的数组
import numpy as np
x = np.empty([3,2], dtype = int)
print(x)
输出结果:
[[0 0]
[0 0]
[0 0]]
numpy.zeros
- 创建指定大小数组,数组元素以0填充
import numpy as np
# 默认为浮点数
x = np.zeros(5)
print(x)
# 设置类型未整数
y = np.zeros((5,), dtype = np.int)
print(y)
# 自定义类型
z = np.zeros((2,2), dtype = [('x', 'i4'),('y','i4')])
print(z)
输出结果:
[0. 0. 0. 0. 0.]
[0 0 0 0 0]
[[(0, 0) (0, 0)]
[(0, 0) (0, 0)]]
numpy.ones
- 创建指定形状的数组,数组元素以1来填充
从已有数组创建
numpy.asarray
import numpy as np
# 将列表转换为ndarray
x = [1,2,3]
a = np.asarray(x)
print(a)
# 将元组转换为ndarray
b = np.asarray(x)
print(b)
# 设置dtype参数
c = np.asarray(x, dtype = float)
print(c)
输出结果:
[1 2 3]
[1 2 3]
[1. 2. 3.]
numpy.frombuffer
- 用于实现动态数组,接受buffer输入参数,以流的形式读入转化成ndarray对象
- 注意,buffer是字符串的时候,Python3默认str是Unicode类型,所以要转成bytestring,在原str前加上b
import numpy as np
s = b'Hello World'
a = np.frombuffer(s, dtype = 'S1')
print(a)
输出结果:
[b'H' b'e' b'l' b'l' b'o' b' ' b'W' b'o' b'r' b'l' b'd']
numpy.fromiter
- 从可迭代对象中建立ndarray对象,返回一维数组
import numpy as np
# 使用range函数创建列表对象
list = range(5)
it = iter(list)
#使用迭代器创建ndarray
x = np.fromiter(it, dtype=float)
print(x)
输出结果:
[0. 1. 2. 3. 4.]
从数值范围创建
numpy.arange
numpy.arrange(start, stop, step, dtype)
import numpy as np
x = np.arange(start=10, stop=20, step=2, dtype=float)
print(x)
输出结果:
[10. 12. 14. 16. 18.]
numpy.linspace
- 用于创建一个等差数列一维数组。
np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
| 参数 | 说明 |
|---|---|
| num | 样本数量,default 50 |
| endpoint | 是否包含终点值,default True |
| retstep | 是否显示间距,default False |
import numpy as np
# 设置不包含终点值
a = np.linspace(10, 20, 5, endpoint = False)
print(a)
# 显示间距
b = np.linspace(1, 10, 10, retstep=True)
print(b)
c = np.linspace(1,10,10)
print(c)
print(c.reshape([10,1]))
输出结果:
[10. 12. 14. 16. 18.]
(array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]), 1.0)
[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
[[ 1.]
[ 2.]
[ 3.]
[ 4.]
[ 5.]
[ 6.]
[ 7.]
[ 8.]
[ 9.]
[10.]]
numpy.logspace
- 用于创建等比数列。
numpy.logspace(start, stop, num, endpoint=True, base=10.0, dtype=None)
| 参数 | 说明 |
|---|---|
| start | 序列的起始值为base**start |
| stop | 序列的终止值为base**stop |
| base | 对数log的底数 |
import numpy as np
a = np.logspace(start=0, stop=9, num=5, base=3)
print(a)
输出结果:
[1.00000000e+00 1.18446661e+01 1.40296115e+02 1.66176064e+03
1.96830000e+04]
1-5 NumPy切片和索引
基本索引方式
import numpy as np
a = np.arange(10)
print(a)
# 通过内置slice函数切割
s = slice(2,7,2) #从索引2开始到索引7结束,间隔为2
print(a[s])
# 通过冒号分隔切片参数start:stop:step切片
print(a[2:7:2])
# 切割多维数组
b = np.array([[1,2,3],[3,4,5],[4,5,6]])
print(b)
print(b[1:]) #选择第二行及之后所有行
print(b[1,1:]) #选择第二行中第二列及之后的所有数
输出结果:
[0 1 2 3 4 5 6 7 8 9]
# 通过内置slice函数切割
[2 4 6]
# 通过冒号分隔切片参数start:stop:step切片
[2 4 6]
# 切割多维数组
[[1 2 3]
[3 4 5]
[4 5 6]]
#选择第二行及之后所有行
[[3 4 5]
[4 5 6]]
#选择第二行中第二列及之后的所有数
[4 5]
n≥3维度数组的索引
注意:使用[]进行数组索引是是从后往前索引的,即从中括号最外层向内进行索引,以下示例说明了这个问题。
import numpy as np
a = np.arange(8).reshape(2,2,2)
print ('原数组:')
print (a)
print ('获取数组中一个值:')
print(np.where(a==6))
print(a[1,1,0]) # 索引为[1,1,0],坐标为(0,0,1)
print ('\n')
输出结果:
原数组:
[[[0 1]
[2 3]]
[[4 5]
[6 7]]]
获取数组中一个值:
(array([1], dtype=int64), array([1], dtype=int64), array([0], dtype=int64))
6
高级索引
整数数组索引
以下实例获取数组中(0,0),(1,1)和(2,0)位置处的元素。
import numpy as np
x = np.array([[1,2],[3,4],[5,6]])
y = x[[0,1,2],[0,1,0]]
print(y)
##这里没太看懂
m = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
print ('我们的数组是:' )
print (m)
print ('\n')
rows = np.array([[0,0],[3,3]])
cols = np.array([[0,2],[0,2]])
n = m[rows,cols]
print ('这个数组的四个角元素是:')
print (n)
输出结果:
[1 4 5]
我们的数组是:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
这个数组的四个角元素是:
[[ 0 2]
[ 9 11]]
布尔索引
import numpy as np
x = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
print ('我们的数组是:')
print (x)
print ('\n') # 现在我们会打印出大于 5 的元素
print ('大于 5 的元素是:')
print (x[x > 5])
#使用取补运算符~
a = np.array([np.nan, 1,2,np.nan,3,4,5])
print (a[~np.isnan(a)])
输出结果:
我们的数组是:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
大于 5 的元素是:
[ 6 7 8 9 10 11]
[1. 2. 3. 4. 5.]
花式索引
花式索引指的是利用整数数组进行索引。
花式索引根据索引数组的值作为目标数组的某个轴的下标来取值。对于使用一维整型数组作为索引,如果目标是一维数组,那么索引的结果就是对应位置的元素;如果目标是二维数组,那么就是对应下标的行。
花式索引跟切片不一样,它总是将数据复制到新数组中。
import numpy as np
x=np.arange(32).reshape((8,4))
print (x[np.ix_([1,5,7,2],[0,3,1,2])])
输出结果:
[[ 4 7 5 6]
[20 23 21 22]
[28 31 29 30]
[ 8 11 9 10]]
注意:x[np.ix_([1,5,7,2],[0,3,1,2])]这句话会输出一个4*4的矩阵,其中的元素分别是:
x[1,0] x[1,3] x[1,1] x[1,2]
x[5,0] x[5,3] x[5,1] x[5,2]
x[7,0] x[7,3] x[7,1] x[7,2]
x[2,0] x[2,3] x[2,1] x[2,2]
2 - NumPy运算
2-1 Broadcast
(Broadcast)是 numpy 对不同形状(shape)的数组进行数值计算的方式, 对数组的算术运算通常在相应的元素上进行。
如果两个数组 a 和 b 形状相同,即满足 a.shape == b.shape,那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同,且各维度的长度相同。
当运算中的数组形状不同时,将会自动触发broadcast机制。
import numpy as np
a = np.array([[ 0, 0, 0],
[10,10,10],
[20,20,20],
[30,30,30]])
b = np.array([1,2,3])
print(a + b)
输出结果:
[[ 1 2 3]
[11 12 13]
[21 22 23]
[31 32 33]]
等效运算:
import numpy as np
a = np.array([[ 0, 0, 0], [10,10,10], [20,20,20], [30,30,30]])
b = np.array([1,2,3])
bb = np.tile(b, (4, 1)) # 重复 b 的各个维度
print(a + bb)
Rules for broadcast
- 规则1:如果两个数组的维度数不相同,那么小维度数组的形状会在最左边补1
- 规则2:如果两个数组的形状在任何一个维度上都不匹配,那么数组的形状会沿着维度为1的维度扩展以匹配另外一个数组的形状
- 规则3:如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于1,那么会引发异常
2-2 迭代数组
迭代访问顺序
默认访问顺序
import numpy as np
a = np.arange(6).reshape(2,3)
print(a)
for x in np.nditer(a):
print(x, end=",")
输出结果:
[[0 1 2]
[3 4 5]]
0,1,2,3,4,5,
以上实例不是使用标准 C 或者 Fortran 顺序,选择的顺序是和数组内存布局一致的,这样做是为了提升访问的效率,默认是行序优先(row-major order,或者说是 C-order)。 这反映了默认情况下只需访问每个元素,而无需考虑其特定顺序。
我们可以通过迭代上述数组的转置来看到这一点,并与以 C 顺序访问数组转置的 copy 方式做对比,如下实例:
import numpy as np
a = np.arange(6).reshape(2,3)
print(a)
print("使用默认方式:")
for x in np.nditer(a):
print(x, end=",")
print("\n转置:\n",a.T)
print('转置后迭代访问顺序与默认相同:')
for x in np.nditer(a.T):
print(x, end=",")
print("\n使用以C顺序访问数组转置的copy方式:")
for x in np.nditer(a.T.copy(order='c')):
print(x, end=",")
输出结果:
[[0 1 2]
[3 4 5]]
使用默认方式:
0,1,2,3,4,5,
转置:
[[0 3]
[1 4]
[2 5]]
转置后迭代访问顺序与默认相同:
0,1,2,3,4,5,
使用以C顺序访问数组转置的copy方式:
0,3,1,4,2,5,
指定访问顺序
import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print ('原始数组是:')
print (a)
print ('\n以 C 风格顺序排序:')
for x in np.nditer(a, order = 'C'):
print (x, end=", " )
print ('\n以 F 风格顺序排序:')
for x in np.nditer(a, order = 'F'):
print (x, end=", " )
输出结果:
原始数组是:
[[ 0 5 10 15]
[20 25 30 35]
[40 45 50 55]]
以 C 风格顺序排序:
0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55,
以 F 风格顺序排序:
0, 20, 40, 5, 25, 45, 10, 30, 50, 15, 35, 55,
修改数组中元素的值
nditer 对象有另一个可选参数 op_flags。 默认情况下,nditer 将视待迭代遍历的数组为只读对象(read-only),为了在遍历数组的同时,实现对数组元素值得修改,必须指定 read-write 或者 write-only 的模式。
import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print(a)
for x in np.nditer(a, op_flags=['readwrite']):
x[...]=2*x # 必须使用x[...]而不是x=2*x
print(a)
输出结果
[[ 0 5 10 15]
[20 25 30 35]
[40 45 50 55]]
[[ 0 10 20 30]
[ 40 50 60 70]
[ 80 90 100 110]]
使用外部循环
- 使用flags参数遍历列值:
| 参数 | 说明 |
|---|---|
| c_index | 可以跟踪C顺序的索引 |
| f_index | 可以跟踪Fortran顺序的索引 |
| multi-index | 每次迭代可以跟踪一种索引类型 |
| external_loop | 给出的值是具有多个值的一维数组,而不是一个一个的数 |
import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print(a)
for x in np.nditer(a, flags=['external_loop'], order='F'):
print(x)
输出结果:
[[ 0 5 10 15]
[20 25 30 35]
[40 45 50 55]]
[ 0 20 40]
[ 5 25 45]
[10 30 50]
[15 35 55]
广播迭代
如果两个数组是可广播的,nditer 组合对象能够同时迭代它们。 假设数组 a 的维度为 3X4,数组 b 的维度为 1X4 ,则使用以下迭代器(数组 b 被广播到 a 的大小)。
import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print(a)
b = np.array([1,2,3,4], dtype = int)
print(b)
for x,y in np.nditer([a,b]):
print("%d:%d" % (x,y),end=",")
输出结果:
[[ 0 5 10 15]
[20 25 30 35]
[40 45 50 55]]
[1 2 3 4]
0:1,5:2,10:3,15:4,20:1,25:2,30:3,35:4,40:1,45:2,50:3,55:4,
2-3 数组运算
NumPy数组操作
修改数组形状
| expression | description |
|---|---|
| reshape(arr, newshape, order=‘C’) | 可以通过order参数指定顺序 |
| flat | ndarray.flat是一个数组元素迭代器 |
| flatten(order=‘C’) | order:‘C’ – 按行,‘F’ – 按列,‘A’ – 原顺序,‘K’ – 元素在内存中的出现顺序 |
| numpy.ravel(a, order=‘C’) | 返回的是数组视图(view,有点类似 C/C++引用reference的意味),修改会影响原始数组。 |
另一种常见的修改数组形状的操作是为已有的数组建立新的空白轴,可以通过简单地在一个切片中使用np.newaxis达成,例如:
import numpy as np
a = np.array([1,2,3])
b = a.reshape((1,3))
c = a[:, np.newaxis]
d = a[np.newaxis, :]
print(a)
print(b)
print(c)
print(d)
输出结果:
[1 2 3]
[[1 2 3]]
# a[:, np.newaxis] 在最内层新建轴
[[1]
[2]
[3]]
# a[np.newaxis, :] 在最外层新建轴
[[1 2 3]]
翻转数组
| expression | description |
|---|---|
| transpose(arr, axes) | 整数列表,对应维度,通常所有维度都会对换 |
| ndarray.T | =self.transpose() |
| rollaxis(arr, axis, start=0) | 向后滚动指定的轴,start默认为零,表示完整的滚动。会滚动到特定位置 |
| swapaxes | 对换数组的两个轴 |
import numpy as np
# 创建了三维的 ndarray
a = np.arange(8).reshape(2,2,2)
print ('原数组:')
print (a)
print ('获取数组中一个值:')
print(np.where(a==6))
print(a[1,1,0]) # 为 6
print ('\n') # 将轴 2 滚动到轴 0(宽度到深度)
print ('调用 rollaxis 函数:')
b = np.rollaxis(a,2,0)
print (b)
# 查看元素 a[1,1,0],即 6 的坐标,变成 [0, 1, 1]
# 最后一个 0 移动到最前面
print(np.where(b==6))
print ('\n')
# 将轴 2 滚动到轴 1:(宽度到高度)
print ('调用 rollaxis 函数:')
c = np.rollaxis(a,2,1)
print (c)
# 查看元素 a[1,1,0],即 6 的坐标,变成 [1, 0, 1]
# 最后的 0 和 它前面的 1 对换位置
print(np.where(c==6))
print ('\n')
输出结果:
原数组:
[[[0 1]
[2 3]]
[[4 5]
[6 7]]]
获取数组中一个值:
(array([1], dtype=int64), array([1], dtype=int64), array([0], dtype=int64))
6
调用 rollaxis 函数:
[[[0 2]
[4 6]]
[[1 3]
[5 7]]]
(array([0], dtype=int64), array([1], dtype=int64), array([1], dtype=int64))
调用 rollaxis 函数:
[[[0 2]
[1 3]]
[[4 6]
[5 7]]]
(array([1], dtype=int64), array([0], dtype=int64), array([1], dtype=int64))
修改数组维度
| expression | description |
|---|---|
| broadcast(x,y) | 对y广播x,拥有 iterator 属性,基于自身组件的迭代器元组 |
| numpy.broadcast_to(array, shape, subok) | 将数组广播到新形状。它在原始数组上返回只读视图。 |
| numpy.expand_dims(arr, axis=0) | axis:新轴插入的位置(before) |
| numpy.squeeze(arr, axis=0) | axis:整数或整数元组,用于选择形状中一维条目的子集 |
连接数组
| expression | description |
|---|---|
| numpy.concatenate((a1, a2, …), axis=0) | 用于沿指定轴连接相同形状的两个或多个数组 |
| numpy.stack(arrays, axis) | axis:返回数组中的轴,输入数组沿着它来堆叠 |
| numpy.hstack | numpy.stack 函数的变体,它通过水平堆叠来生成数组 |
import numpy as np
a = np.array([
[1,2],
[3,4]
])
b = np.array([
[5,6],
[7,8]
])
c = np.concatenate((a,b), axis=1)
d = np.hstack((a,b))
print(c==d)
e = np.concatenate((a,b))
print(e)
print(',e.shape, '>\n')
f = np.stack((a,b), axis=0)
print(f)
print(',f.shape,'>\n')
g = np.stack((a,b), axis=1)
print(g)
print(',g.shape,'>')
输出结果:
# c = np.concatenate((a,b), axis=1)
# d = np.hstack((a,b))
[[ True True True True]
[ True True True True]]
# e = np.concatenate((a,b))
[[1 2]
[3 4]
[5 6]
[7 8]]
<shape of e: (4, 2) >
# f = np.stack((a,b), axis=0)
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
<shape of f: (2, 2, 2) >
# g = np.stack((a,b), axis=1)
[[[1 2]
[5 6]]
[[3 4]
[7 8]]]
<shape of g: (2, 2, 2) >
以上结果可以简单理解为:
- 对于二维数组,在axis=1上进行拼接(concatenate)等同于使用hstack函数
- stack函数将会增加维度,axis参数确定了拼接后列和深度的位置,axis=0时厚度即为深度,axis=1时原来的列变为深度。
分割数组
| expression | description |
|---|---|
| numpy.split(ary, indices_or_sections, axis=0) | 将一个数组分割为多个子数组;indices_or_sections:如果是一个整数,就用该数平均切分,如果是一个数组,为沿轴切分的位置(左开右闭) |
| hsplit | 将一个数组水平分割为多个子数组(按列) |
| vsplit | 将一个数组垂直分割为多个子数组(按行) |
数组元素的添加与删除
| expression | description |
|---|---|
| numpy.resize(arr, shape) | 回指定大小的新数组。如果新数组大小大于原始大小,则包含原始数组中的元素的副本。 |
| numpy.append(arr, values, axis=None) | 在数组的末尾添加值 |
| numpy.insert(arr, obj, values, axis) | 在给定索引之前,沿给定轴在输入数组中插入值;如果未提供轴,则输入数组会被展开 |
| Numpy.delete(arr, obj, axis) | 返回从输入数组中删除指定子数组的新数组。 与 insert() 函数的情况一样,如果未提供轴参数,则输入数组将展开。 |
| numpy.unique(arr, return_index, return_inverse, return_counts) | 用于去除数组中的重复元素 |
import numpy as np
a = np.array([[1,2,3],[4,5,6]])
print ('第一个数组:')
print (a)
print ('\n')
print ('向数组添加元素:')
print (np.append(a, [7,8,9]))
print ('\n')
print ('沿轴 0 添加元素:')
print (np.append(a, [[7,8,9]],axis = 0))
print ('\n')
print ('沿轴 1 添加元素:')
print (np.append(a, [[5,5],[7,8]],axis = 1))
输出结果:
第一个数组:
[[1 2 3]
[4 5 6]]
向数组添加元素:
[1 2 3 4 5 6 7 8 9]
沿轴 0 添加元素:
[[1 2 3]
[4 5 6]
[7 8 9]]
沿轴 1 添加元素:
[[1 2 3 5 5]
[4 5 6 7 8]]
2-4 位运算
(略)
3 - 常用函数
3-1 字符串函数
待补充
3-2 数学函数
三角函数
指数和对数
| expression | description |
|---|---|
| np.exp(x) | e x e^x ex |
| np.exp2(x) | 2 x 2^x 2x |
| np.power(x, y) | x y x^y xy |
| np.log(x) | ln x \ln{x} lnx |
| np.log10(x) | log 10 x \log_{10}{x} log10x |
| np.log2(x) | log 2 x \log_{2}{x} log2x |
| np.expm1(x) | e x − 1 e^x-1 ex−1 |
| np.log1p(x) | ln ( 1 + x ) \ln{(1 + x)} ln(1+x) |
| np.logaddexp(a,b) | log ( e a + e b ) \log{(e^a+e^b)} log(ea+eb) |
3-3 算术函数
python运算符对应表:
| Python运算符 | NumPy通用函数 | 描述 |
|---|---|---|
| + | np.add | 加法运算 |
| - | np.subtract | 减法运算 |
| - | np.negative | 负数运算 |
| * | np.multiply | 乘法运算 |
| / | np.divide | 除法运算 |
| // | np.floor_divide | 向下整除运算 |
| ** | np.power | 指数运算 |
| % | np.mod | 模 |
| abs() | np.absolute/np.abs | 绝对值 |
3-4 统计函数
| expression | description |
|---|---|
| numpy.amin(arr, axis=None) | 计算数组中的元素沿指定轴的最小值 |
| numpy.amax(arr, axis=None) | 计算数组中的元素沿指定轴的最大值 |
| numpy.ptp() | 计算数组中元素最大值与最小值的差(最大值 - 最小值) |
| numpy.percentile(arr, q, axis=None) | q: 要计算的百分位数,在 0 ~ 100 之间 |
| numpy.median(arr, axis) | 中位数 |
| numpy.mean() | 均值 |
| numpy.average(a, axis=None, weights=None, returned=False) | 根据在另一个数组中给出的各自的权重计算数组中元素的加权平均值 |
| numpy.std() | 标准差 |
| numpy.var() | 样本方差 |
专用的通用函数
除了上述常用函数,NumPy还提供了很多通用函数,包括双曲三角函数、比特位运算、比较运算符、弧度转化为角度的运算、取整和求余运算等。还有一个更加专用的通用函数来源,就是子模块scipy.special,例如Gamma函数、高斯积分等等。
3-5 排序、条件筛选函数
NumPy提供了多种排序函数,这些排序函数实现不同的排序算法,每个排序算法的特征在于执行速度、最坏情况性能、所需的工作空间和算法稳定性。
numpy.sort()
返回输入数组的排序副本。
numpy.sort(a, axis, kind, order)
- axis: 如果没有,数组会被展开,沿着最后的轴排序
- kind: 默认为’quicksort’(快速排序)
- order: 如果数组包含字段,则是要排序的字段
import numpy as np
a = np.random.randn(3,3,3).round(2)
print(a)
print(np.sort(a)) # 按行排序(最里面一层)
print(np.sort(a, axis=0)) # 按深度排序(最外面一层)
print(np.sort(a, axis=1)) # 按中间层排序
numpy.lexsort()
用于对多个序列进行排序,排序时优先照顾靠后的列,相当于按照多个维度进行排序,返回索引序列。
import numpy as np
nm = ('raju','anil','ravi','amar')
dv = ('f.y.', 's.y.', 's.y.', 'f.y.')
ind = np.lexsort((dv,nm))
print ('调用 lexsort() 函数:')
print (ind)
print ('使用这个索引来获取排序后的数据:')
print ([nm[i] + ", " + dv[i] for i in ind]) # 小技巧
输出结果:
调用 lexsort() 函数:
[3 1 0 2]
使用这个索引来获取排序后的数据:
['amar, f.y.', 'anil, s.y.', 'raju, f.y.', 'ravi, s.y.']
np.msort(a)
按第一个轴排序(最外面一层),等价于np.sort(a, axis=0)
sort_complex(a)
对复数按照先实部后虚部的顺序进行排序。
partition(a, kth[, axis, kind, order])
指定一个数,对数组进行分区。
import numpy as np
arr = np.array([46,57,23,39,1,10,0,120])
print(arr)
## partition的规则是先分区后排序
print(np.partition(arr, 2)) #表示比29小的数排前面,比29大的数排后面
输出结果:
[ 46 57 23 39 1 10 0 120]
[ 0 1 10 39 57 23 46 120]
index functions
返回序列值
numpy.argmax()和numpy.argmin()
沿指定轴返回最大值和最小值的索引。
numpy.argsort()
返回数组值从小到大的索引值。
import numpy as np
a = np.random.randn(3,3,3).round(2)
print(a)
print(np.argsort(a)) # 按行排序(最里面一层)
print(np.argsort(a, axis=0)) # 按深度排序(最外面一层)
print(np.argsort(a, axis=1)) # 按中间层排序
输出结果:
[[[ 0.75 -0.7 -0.34]
[ 1.18 -0.1 1.14]
[-0.6 -1.18 -1.15]]
[[ 0.67 -0.5 0.11]
[ 1.04 -0.86 -0.07]
[ 0.71 -0.57 -1.26]]
[[ 1.57 -0.55 -0.56]
[-0.08 -0.19 -0.34]
[ 0.05 0.01 -0.01]]]
[[[1 2 0]
[1 2 0]
[1 2 0]]
[[1 2 0]
[1 2 0]
[2 1 0]]
[[2 1 0]
[2 1 0]
[2 1 0]]]
[[[1 0 2]
[2 1 2]
[0 0 1]]
[[0 2 0]
[1 2 1]
[2 1 0]]
[[2 1 1]
[0 0 0]
[1 2 2]]]
[[[2 2 2]
[0 0 0]
[1 1 1]]
[[0 1 2]
[2 2 1]
[1 0 0]]
[[1 0 0]
[2 1 1]
[0 2 2]]]
argpartition(a, kth[, axis, kind, order])
可以通过关键字kind指定算法沿着指定轴对数组进行分区,返回的是一个索引序列。
numpy.nonzero()
返回数组中非零元素的索引。
numpy.where()
返回数组中满足给定条件的元素的索引。
import numpy as np
a = np.random.randn(3,3,3).round(2)
print(a)
m = a.flatten().mean()
print(m)
print(a[np.where(a>m)]) # 获取大于均值的元素(返回列表)
输出结果:
[[[ 0.96 -0.39 -0.54]
[-0.36 -0.07 -0.61]
[-0.82 1.04 -0.24]]
[[-0.38 1.49 0.6 ]
[ 0.57 -0.45 1.26]
[-0.64 0.5 -1.3 ]]
[[-1.5 -0.7 -0.66]
[ 0.73 -0.46 0.94]
[-0.43 -2.01 -1.79]]]
-0.19481481481481483
[ 0.96 -0.07 1.04 1.49 0.6 0.57 1.26 0.5 0.73 0.94]
numpy.extract()
根据某个条件从数组中抽取元素。
import numpy as np
a = (100*np.random.randn(3,3,3).round(2))
print(a)
condition = np.mod(a,3)==1 # 满足模3余1
print(condition)
print(np.extract(condition,a)) # 获取满足条件的元素
输出结果:
[[[ -73. -112. 148.]
[ 44. -57. 9.]
[ 161. -53. -93.]]
[[ -61. -31. 88.]
[-193. 82. -16.]
[ 147. 13. 80.]]
[[ 18. -5. 32.]
[-283. -40. -20.]
[ 114. 1. 39.]]]
[[[False False True]
[False False False]
[False True False]]
[[False False True]
[False True False]
[False True False]]
[[False True False]
[False False True]
[False True False]]]
[148. -53. 88. 82. 13. -5. -20. 1.]
4 - 扩展
4-1 字节交换
(略)
4-2 副本和视图
副本是一个数据的完整的拷贝,如果我们对副本进行修改,它不会影响到原始数据,物理内存不在同一位置。
视图是数据的一个别称或引用,通过该别称或引用亦便可访问、操作原有数据,但原有数据不会产生拷贝。如果我们对视图进行修改,它会影响到原始数据,物理内存在同一位置。
赋值
赋值不会创建数组对象的副本,它会使用原始数组的相同id()来访问它,因此,被赋值对象的任何改变都会同时影响原始对象。
视图/浅拷贝
ndarray.view()方法会创建一个新的数组对象,更改新的数组形状不会影响到原始数据的形状。
import numpy as np
a = (100*np.random.randn(1,3,4).round(2))
# 视图对象与原数组存储位置不同
print(id(a))
print(a[0,0,0])
b = a.view()
print(id(b))
# 修改视图对象的形状不会影响到原数组
b.shape = (2,2,3)
print(b.shape)
print(a.shape)
# 修改内容会影响到原始数据
b[0,0,0] += 1
print(b[0,0,0])
print(b[0,0,0]==a[0,0,0])
输出结果:
# 视图对象与原数组存储位置不同
1958816723472
-68.0
1958816723552
# 修改视图对象的形状不会影响到原数组
(2, 2, 3)
(1, 3, 4)
# 修改内容会影响到原始数据
-67.0
True
切片器原理也是创建视图,修改视图将影响到原始数组。
副本/深拷贝
ndarray.copy()创建一个副本。对副本数据进行修改不会影响到原始数据,它们物理内存不在同一位置。
4-3 矩阵库
NumPy中包含了一个矩阵库numpy.matlib,该模块中的函数返回的是一个矩阵,而不是ndarray对象。
这个库快要废掉了,建议不要用。
转置矩阵
ndarray.T
matlib.empty()
返回一个随机数填充的矩阵。
numpy.matlib.empty(shape, dtype, order)
- shape: 整数或整数元组
- order: C(行序优先)或F(列序优先)
matlib.zeros()
返回一个零矩阵。
matlib.ones()
返回一个以1填充的矩阵。
matlib.eye()
返回一个广义的对角矩阵。
numpy.matlib.eye(n, M,k, dtype)
- n: 行数
- M: 列数,默认为n
- k:对角线索引
import numpy as np
import numpy.matlib
a = np.matlib.eye(n = 3, M = 4, k = 1)
print(a)
输出结果:
[[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
matlib.identity()
返回给定大小的单位矩阵。
4-4 线性代数
NumPy提供了线性代数函数库linalg,包含了线性代数所需的所有功能
numpy.dot()
简单记一下,dot()计算二维矩阵的矩阵乘积。
numpy.dot(a, b, out=None)
- numpy.dot() 对于两个一维的数组,计算的是这两个数组对应下标元素的乘积和(数学上称之为内积);对于二维数组,计算的是两个数组的矩阵乘积;对于多维数组,它的通用计算公式如下,即结果数组中的每个元素都是:数组a的最后一维上的所有元素与数组b的倒数第二维上的所有元素的乘积和:
dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])
numpy.vdot()
计算两个向量的内积。如果第一个参数是复数,那么它的共轭复数会用于计算。如果参数是多维数组,将自动展开计算。
numpy.inner()
- 对于一维数组,返回向量内积;
- 对于n>=2,返回最后一个轴上的和的乘积。
numpy.matmul()
numpy.matmul 函数返回两个数组的矩阵乘积。虽然它返回二维数组的正常乘积,但如果任一参数的维数大于2,则将其视为存在于最后两个索引的矩阵的栈,并进行相应广播。
另一方面,如果任一参数是一维数组,则通过在其维度上附加 1 来将其提升为矩阵,并在乘法之后被去除。
对于二维数组,它就是矩阵乘法。
numpy.linalg.det()
计算矩阵行列式。
numpy.linalg.solve()
给出了矩阵形式的线性方程的解。
numpy.linalg.inv()
计算逆矩阵(inverse matrix)。
import numpy as np
a = np.array([
[1,1,1],
[0,2,5],
[2,5,-1]
])
b = np.array([6,-4,27])
print(a)
print(b)
# 解法1:
x = np.linalg.solve(a,b)
print(x)
# 解法2:
## 求逆矩阵
ainv = np.linalg.inv(a)
print(ainv)
## 逆矩阵*向量b
y = np.dot(ainv,b)
print(y)
print(x==y)
输出结果:
[[ 1 1 1]
[ 0 2 5]
[ 2 5 -1]]
[ 6 -4 27]
[ 5. 3. -2.]
[[ 1.28571429 -0.28571429 -0.14285714]
[-0.47619048 0.14285714 0.23809524]
[ 0.19047619 0.14285714 -0.0952381 ]]
[ 5. 3. -2.]
[ True False False]
4-5 IO
Numpy 可以读写磁盘上的文本数据或二进制数据。
NumPy 为 ndarray 对象引入了一个简单的文件格式:npy,npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息。
常用的 IO 函数有:
- load() 和 save() 函数是读写文件数组数据的两个主要函数,默认情况下,数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中。
- savez() 函数用于将多个数组写入文件,默认情况下,数组是以未压缩的原始二进制格式保存在扩展名为 .npz 的文件中。
- loadtxt() 和 savetxt() 函数处理正常的文本文件(.txt 等)
numpy.save()
numpy.save(file, arr, allow_pickle=True, fix_imports=True)
- allow_pickle: 可选,布尔值,允许使用 Python pickles 保存对象数组,Python 中的 pickle 用于在保存到磁盘文件或从磁盘文件读取之前,对对象进行序列化和反序列化。
- fix_imports: 可选,为了方便 Pyhton2 中读取 Python3 保存的数据
numpy.savez()
将多个数组保存到以 npz 为扩展名的文件中。
numpy.savez(file, *args, **kwds)
- file:要保存的文件,扩展名为 .npz,如果文件路径末尾没有扩展名 .npz,该扩展名会被自动加上。
- args: 要保存的数组,可以使用关键字参数为数组起一个名字,非关键字参数传递的数组会自动起名为 arr_0, arr_1, … 。
- kwds: 要保存的数组使用关键字名称。
savetxt()
以简单的文本文件格式存储数据,对应的使用 loadtxt() 函数来获取数据。
np.loadtxt(FILENAME, dtype=int, delimiter=’ ')
np.savetxt(FILENAME, a, fmt="%d", delimiter=",")
- delimiter:可以指定各种分隔符、针对特定列的转换器函数、需要跳过的行数等
4-6 Matplotlib
Matplotlib 是 Python 的绘图库。 它可与 NumPy 一起使用,提供了一种有效的 MatLab 开源替代方案。 它也可以和图形工具包一起使用,如 PyQt 和 wxPython。
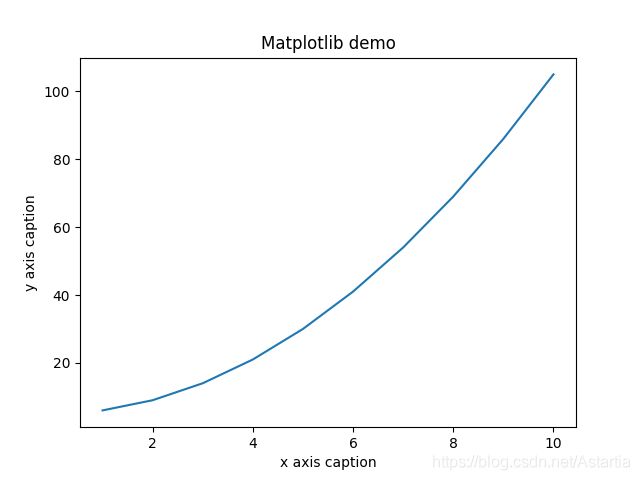
基本操作
import numpy as np
from matplotlib import pyplot as plt
# 基本操作
x = np.arange(1,11)
y = x**2+5
plt.title("Matplotlib demo")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
plt.plot(x,y)
plt.show()
输出结果:
字体设置
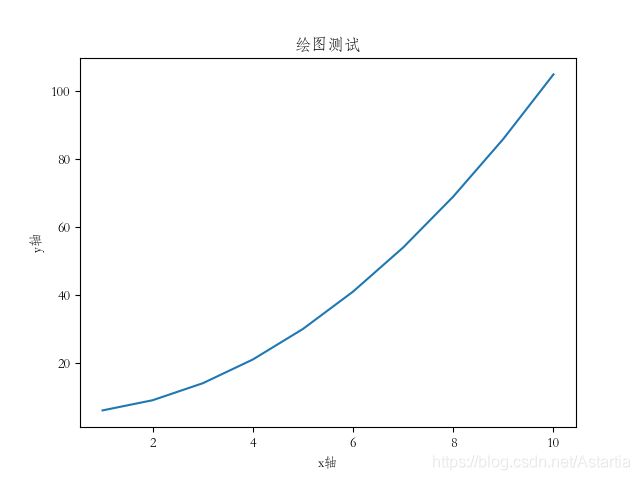
使用官方字体
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1,11)
y = x**2+5
# 获取字体列表
f = sorted([f.name for f in matplotlib.font_manager.fontManager.ttflist])
# 设置中文字体
plt.rcParams['font.family']=['STFangsong']
plt.title("绘图测试")
plt.xlabel("x轴")
plt.ylabel("y轴")
plt.plot(x,y)
plt.show()
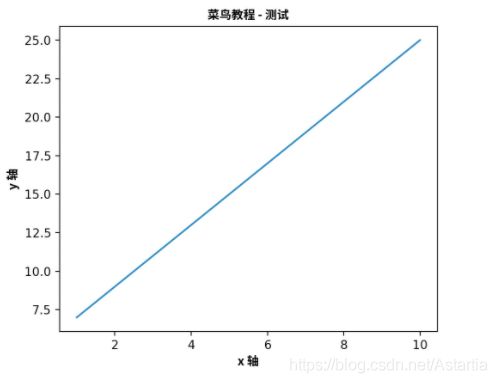
自定义字体文件
import numpy as np
from matplotlib import pyplot as plt
import matplotlib
x = np.arange(1,11)
y = x**2+5
# fname 为 你下载的字体库路径,注意 SourceHanSansSC-Bold.otf 字体的路径
zhfont1 = matplotlib.font_manager.FontProperties(fname="SourceHanSansSC-Bold.otf")
x = np.arange(1,11)
y = 2 * x + 5
plt.title("菜鸟教程 - 测试", fontproperties=zhfont1)
# fontproperties 设置中文显示,fontsize 设置字体大小
plt.xlabel("x 轴", fontproperties=zhfont1)
plt.ylabel("y 轴", fontproperties=zhfont1)
plt.plot(x,y)
plt.show()
绘制散点图
作为线性图的替代,可以通过向 plot() 函数添加格式字符串来显示离散值。
import numpy as np
from matplotlib import pyplot as plt
import matplotlib
x = np.arange(1,11)
y = x**2+5
plt.title("Matplotlib demo")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
plt.plot(x,y,"ob") # 蓝色圆点
plt.show()
还可以设置品红色水平线标记:)
plt.plot(x,y,"_m") # 品红色水平线标记
绘制正弦图
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-np.pi, np.pi, 0.01)
y = np.sin(x)
plt.title("sine wave")
plt.plot(x,y)
plt.show()
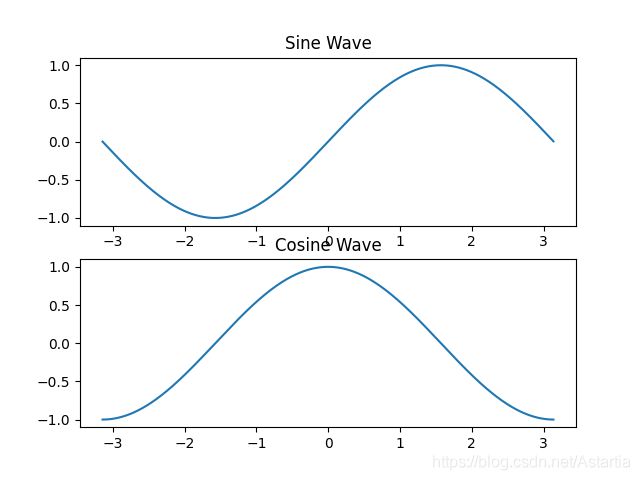
plt.subplot
在同一张图中绘制不同的图形。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-np.pi, np.pi, 0.01)
y1 = np.sin(x)
y2 = np.cos(x)
# 建立subplot网格,高为2,宽为1
plt.subplot(2,1,1) # 激活第一个网格
# 绘制第一个图象
plt.plot(x, y1)
plt.title("Sine Wave")
# 绘制第二个图象
plt.subplot(2,1,2) # 激活第二个网格
plt.plot(x, y2)
plt.title("Cosine Wave")
plt.show()
将图形绘制在同一区域
利用numpy.array(y1,y2).T生成对应shape的数组,并将其整个作为对象放入y轴。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-np.pi, np.pi, 0.01)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x,np.array([y1,y2]).T)
plt.show()
或者使用以下语句,分两次将曲线添加至绘图区域中:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-np.pi, np.pi, 0.01)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x,y1,color='g')
plt.plot(x,y2,color='b')
plt.show()
plt.bar()
from matplotlib import pyplot as plt
x1 = [5,8,10]
y1 = [12,16,6]
x2 = [6,7,9]
y2 = [6,8,7]
plt.bar(x1, y1, align = 'center')
plt.bar(x2, y2, color = 'g', align = 'center')
plt.title('Bar Graph')
plt.ylabel('Population (in million)')
plt.xlabel('Month')
plt.show()
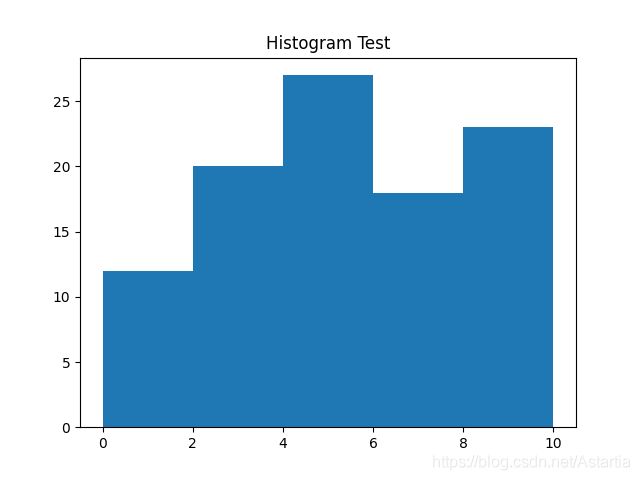
numpy.histogram()与直方图
numpy.histogram()函数是数据的频率分布的图形表示。水平尺寸相等的矩形对应于类间隔,称为bin,变量height对应于频率。
numpy.histogram()将输入数组和bin作为两个参数。bin数组中的连续元素用作每个bin的边界。
import numpy as np
from matplotlib import pyplot as plt
a = np.random.rand(100).round(1)*10
print(a)
b = np.linspace(start=0,stop=10,num=6)
print(b)
# 查看numpy.histogram的内容
h = np.histogram(a, bins = b)
print(h)
# 绘制直方图
plt.hist(a, bins = b)
plt.title("Histogram Test")
plt.show()
输出结果:
[ 0. 2. 4. 6. 8. 10.]
(array([12, 20, 27, 18, 23], dtype=int64), array([ 0., 2., 4., 6., 8., 10.]))