pytorch之卷积神经网络
本文是我在参阅了多方面的博客资源之后的笔记整理，相信我，不需要再寻找其他的资源，只需要认认真真，完完整整的看我这篇博客的内容以及提及的资源，理解torch.nn.Conv1d()和torch.nn.Conv2d()就完全足够。本博客的目的，就是节省你的学习时间，一篇就全！不懂的可以随时评论，帮助解答~
1. 卷积层的理解
卷积层是用一个固定大小的矩形区去席卷原始数据，将原始数据分层一个个和卷积核大小相同的小块，然后将这些小块和卷积核相乘之后再相加输出一个卷积值（注意，这里是一个单独的数值，不再是矩阵了）。
卷积的本质就是使用卷积核的参数来提取原始数据的特征，通过矩阵的点乘运算，提取出和卷积核特征一致的值，如果卷积层有多个卷积核，就会提取多个特征，神经网络会自动学习卷积核的参数值，使得每个卷积核代表一个特征。
【这里可以通过线性代数来理解，将每个卷积核看做是一组特征向量的基，然后通过线性变换，就可以得到在这组特征向量基下获取到的特征】
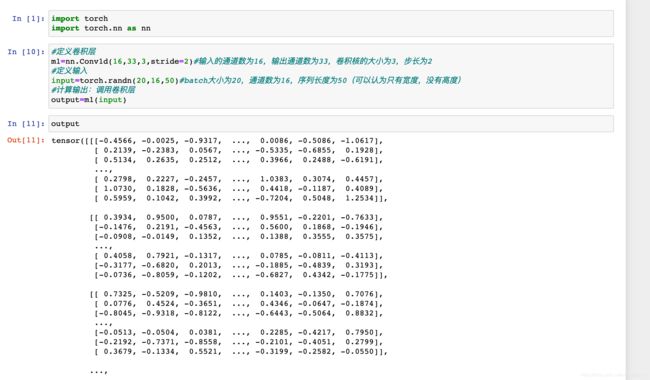
2. torch.nn.Conv2d()
官方文档文档
中文文档
-
输入格式
注意下面的说明：
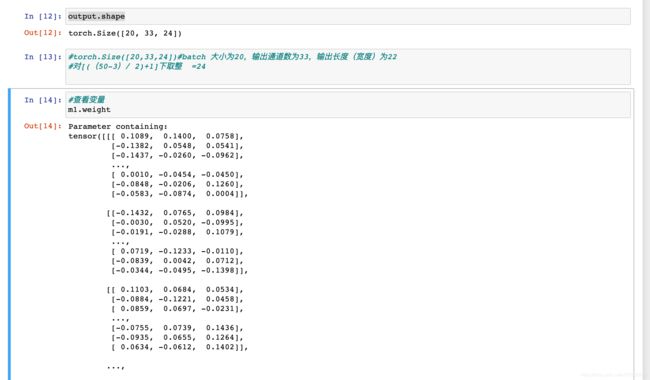
即参数kernel_size, string, padding, dilation 也可以是一个int的数据，此时卷积height和weight的数值相同；也可以是一个tuple数组，tuple的第一维表示height的数值，tuple的第二维表示width的数值。 -
H o u t 和 W o u t 的 计 算 H_{out} 和 W_{out} 的计算 Hout和Wout的计算：
-
参数说明
in_channels （int）:输入信号的通道数
out_channels (int): 卷积产生的通道数
kerner_size (int or tuple, 可选): 卷积核的尺寸 （注意看一下上面的说明）
stride (int or tuple，可选): 卷积的步长
padding （int or tuple，可选）：输入的每一条边补充0的个数
dilation (int or tuple，可选): 卷积核元素之间的间距
groups (int，可选), 从输入通道到输出通道的阻塞连接数
bias(bool,可选)：如果bias=True，添加偏置，默认为True。
默认情况：
def __init__(self, in_channels, out_channels, kernel_size, stride=1,
padding=0, dilation=1, groups=1, bias=True):
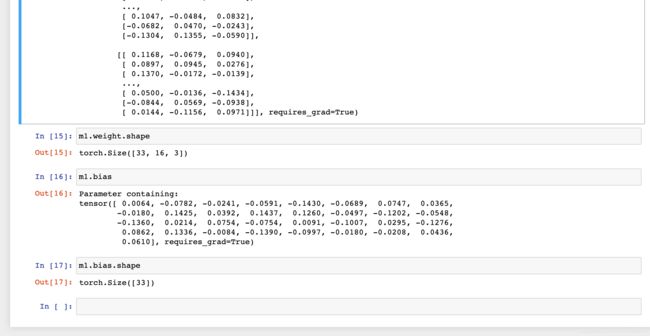
- 变量（可读取和调用）
- 示例：
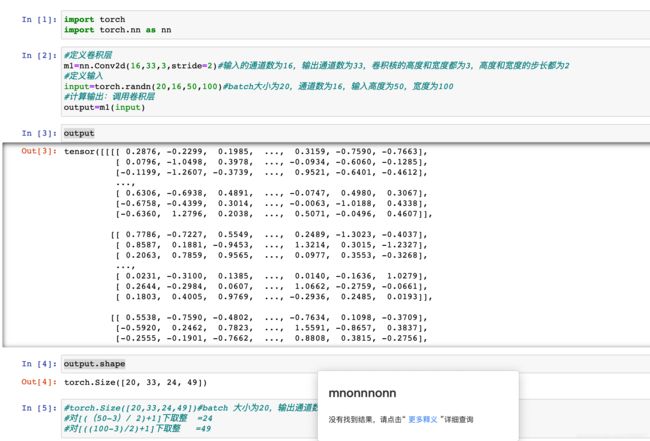保持边界信息，如果没有加padding的话，输入图片最边缘的像素点信息只会被卷积核操作一次，但是图像中间的像素点会被扫描很多遍，那么就会在一定程度上降低边界信息的参考程度，但是在加入padding之后，在实际处理过程中就会从新的边界（加入padding后的边界，这里也就说明了，padding操作是在卷积之前进行的）进行操作，就从一定程度上解决了这个问题。
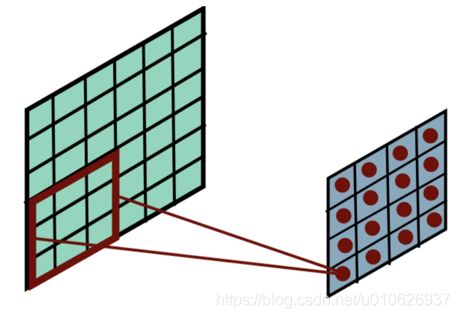
如下图所示，对6x6的原图像使用3x3的卷积核进行卷积操作后得到的图像是一个4x4的图像(6-3+1=4)，也就是说每次进行卷积后，原始图像都会变小失真，所以没有办法设计层数足够多的深度神经网络，除此之外还有另一个重要的原因是，原始图像中的边缘像素永远都不会位于卷积核的中心，只有原始图像的4x4的像素会位于中心，这样会使得边缘像素对网络的影响小于位于中心点的像素的影响，不利于抽取特征。
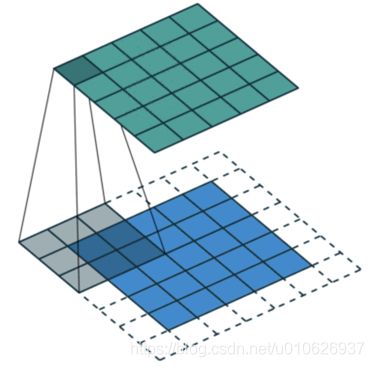
所以，为了解决这个问题，一般会在原始图像的周围填充一圈像素，如下图所示，将原来的输入图像（率），四周各填充一圈0之后吧，就变成了底部的蓝色图，这个时候，原图像的边缘的位置就可以位于卷积核中心了。
另外还有一些其他的用途：
（2）可以在利用padding对属兔尺寸有差异的图片进行不起，使得输入图片尺寸一致。
（3）在卷积神经网络的卷积层加入padding，可以使得卷积层的输入维度和输出维度一致（这只是其中的一个用途，真正的作用还是（1））；在卷积神经网络的池化层加入padding，一般就是保持边界信息。
3.2 通道（channel）的理解
一般的图像都是三通道，分别是R，G, B，所以卷积核也应该为三个通道，通过卷积核作用后生成的图像也会有三个，如图所示：
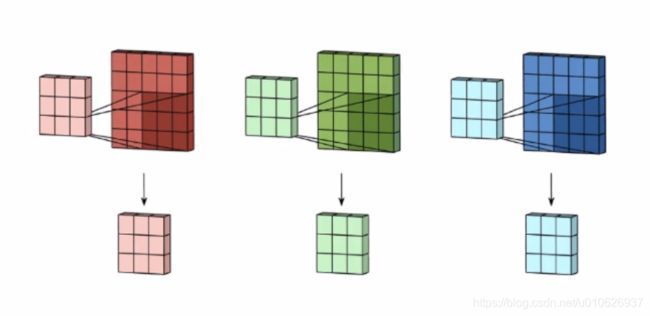
得到三个图像后，然后把这三个图像通过矩阵相加的计算，最后得到一个“合成”图像，如图所示：
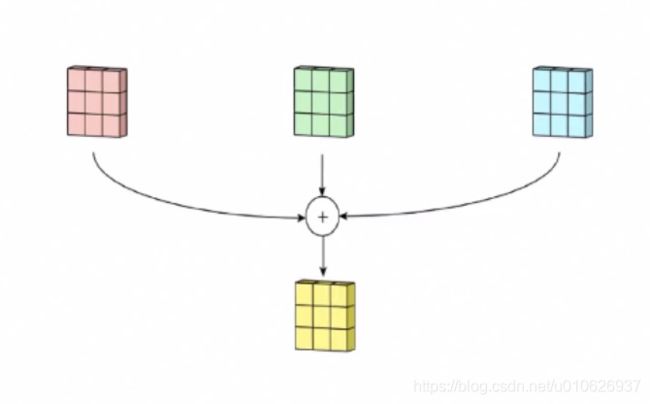
最后，将这个图像与一个偏置项（bias）向加后就会得到一个最终的结果，偏置项不影响结果的矩阵形状，只是影响矩阵的值，如图，
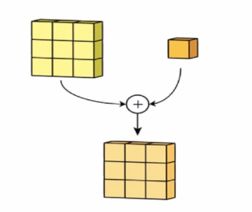
进一步理解：
如果对于一个三通道即：32x32x3的图像，使用一个：5x5x3的卷积核，最终会得到一个：28x28x1的特征图，如图：
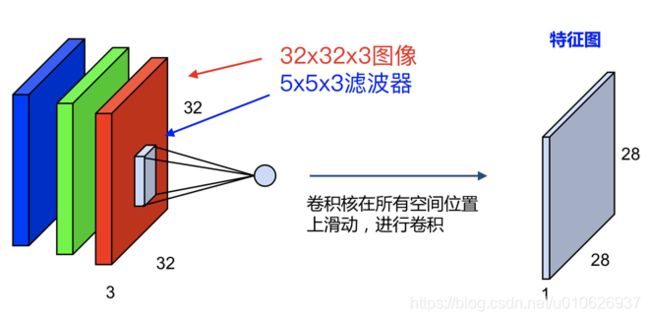
如果使用两个：
5x5x3的卷积核，最终会得到两个：28x28x1的特征图，即：28x28x2，如图：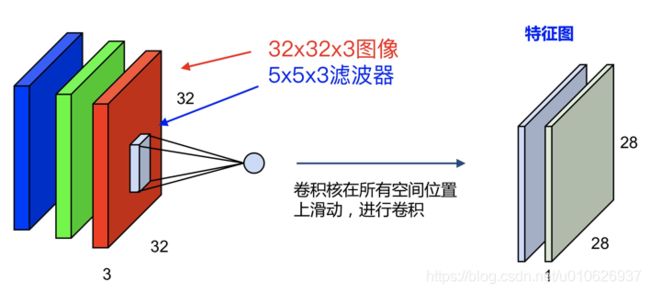
如果使用六个：5x5x3的卷积核，最终会得到六个：28x28x1的特征图，即：28x28x6，如图：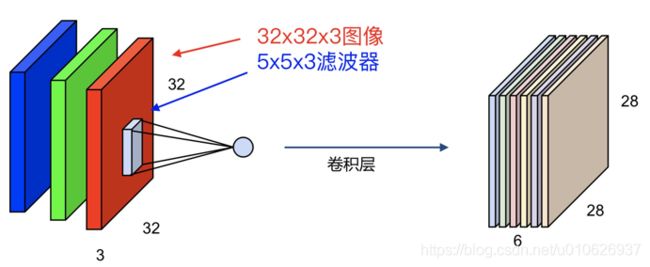
请记住：
卷积过程中，输入层有多少个通道，卷积核就有多少个通道，但是卷积核的数量是任意的，卷积核的数量决定了卷积后特征图的数量。
4. torch.nn.Conv1d()
其实我们平时最常用的就是二维卷积，所以要掌握好二维卷积的用法，一维卷积和三维卷积和二维卷积很相似，论说，应该从一维卷积开始介绍，但是由于二维卷积使用的最多，所以放在前面了；一般来说，一维卷积用于文本数据，二维卷积用于图像数据，三维卷积用于视频数据。
一维卷积可以用于文本数据，只对宽度进行卷积，对高度不卷积。通常，输入大小为word_embedding_dim*max_length，其中word_embedding_dim为词向量的维度大小，max_length为最大句子长度。一维卷积核在句子长度的方向上活动，进行卷积操作。
其参数和二维卷积torch.nn.Conv2d()参数是一样的，其默认形式如下：
class torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
-
官网介绍
-
值得注意的地方：
-
参数
在使用方面，和Conv2d()的最大不同之处在于in_channels、out_channels、kernel_size的大小。
-
示例
其实，一维的卷积可以看做是高度为1的二维卷积，举例说明一下：
进一步应用实例说明
一维卷积 torch.nn.Conv1d()在文本上的应用
class torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
- in_channels:z在文本应用中，即为词向量的维度。
- out_channels:卷积产生的通道数，有多少个out_channels, 就需要多少个一维卷积（也就是卷积核的数据量）;
- kernel_size:卷积核的尺寸；卷积核的第二个维度由in_channels决定，所以实际上卷积核的大小为kernel_size*in_channels
- padding:对输入的每一条边，补充0的层数。
任务：
输入：批大小为32，句子最大长度为35，词向量的维度为256；
目标：句子分类，共2类。
#基于卷积的文本分类实例
import torch
import torch.nn as nn
import torch.nn.functional as F
#这句coding定义了多个窗口的卷积
convs=nn.ModuleList([nn.Sequential(nn.Conv1d(in_channels=5,out_channels=100,kernel_size=h),
nn.ReLU(),
nn.MaxPool1d(kernel_size=35-h+1))
for h in [2,3,4]])
#conv1=nn.Conv1d(in_channels=256,out_channels=100,kernel_size=(2,3,4))
fc=nn.Linear(in_features=100*3,out_features=2)
input=torch.randn(32,35,256)
print(input.shape)
input=input.permute(0,2,1)
print(input.shape)
output=[conv(input) for conv in convs]
print(output[0].shape)
print([out.shape for out in output])
output=torch.cat(output,dim=1)
print(output.shape)
output=output.view(-1,output.size(1))
out=F.dropout(input=output,p=0.3)
out=fc(out)
print(out.shape)
假设window_size = [2,3, 4]，即共有四个卷积核，基于上述代码，具体计算过程如下：
- 原始输入大小为(32, 35, 256)，经过permute(0, 2, 1)操作后，输入的大小变为(32, 256, 35)；
- 使用1个卷积核进行卷积，可得到1个大小为32 x 100 x 1的输出，共4个卷积核，故共有4个大小为32 x 100 x 1的输出；
- 将上一步得到的4个结果在dim = 1上进行拼接，输出大小为32 x 300 x 1；
- view操作后，输出大小变为32 x 300；
- 全连接，最终输出大小为32 x 2，即分别预测为2类的概率大小。
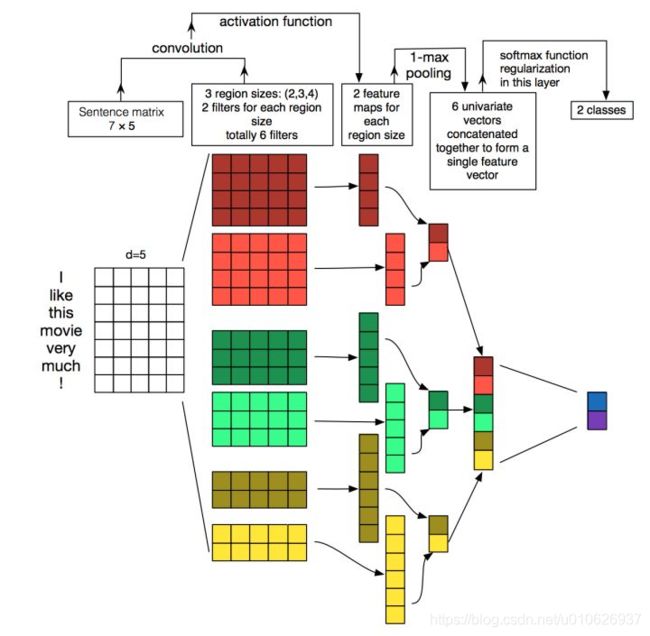
一维卷积的图解过程
Yoon Kim在2014年发表的论文Convolutional Neural Networks for Sentence Classification中，给出了一个非常形象的图，诠释了文本卷积模型的框架，如下所示。
二维卷积torch.nn.Conv2d()在图像上的应用。
class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
任务：
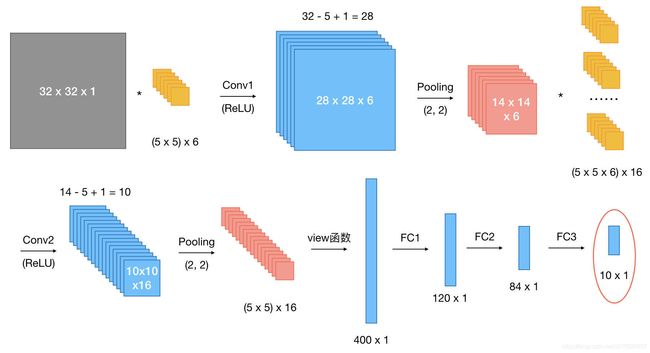
假设现有大小为32 x 32的图片样本，输入样本的channels为1，该图片可能属于10个类中的某一类。
我们假设整体的网络结构为：[conv + relu +pooling]2 +FC3
原始输入样本的大小为：[1,1,32,32]:batch数为1，通道数为1，高度为32，宽度为32
代码如下：
#基于卷积的图片分类，这次以类函数的方式给出，比较符合平时的实验设计
import torch
import torch.nn as nn
import torch.nn.functional as F
class CNN(nn.Module):
def __init__(self):
nn.Module.__init__(self)
self.conv1=nn.Conv2d(1,6,5)#第一个卷积层
self.conv2=nn.Conv2d(6,16,5)#第二个卷积层
self.fc1=nn.Linear(5*5*16,120)
self.fc2=nn.Linear(120,84)
self.fc3=nn.Linear(84,10)
def forward(self,x):
#输入x -> conv1 -> relu ->2*2 窗口的最大池化
x=self.conv1(x)
x=F.relu(x)
x=F.max_pool2d(x,2)
#输入x ->conv2 ->relu ->2*2窗口的最大池化
x=self.conv2(x)
x=F.relu(x)
x=F.max_pool2d(x,2)
x=x.view(x.size()[0],-1)
x=F.relu(self.fc1(x))
x=F.relu(self.fc2(x))
x=self.fc3(x)
return x
x=torch.randn(1,1,32,32)
model=CNN()
y=model(x)
print(y.shape)
二维卷积的图解过程
#注意
- 在pytorch 中，池化操作默认的stride大小与卷积核的大小一致；
- 如果池化核的大小为一个方阵，则仅需要指明一个数，即，kenel_size参数为常数n,表示池化核大小为n*n。