植物大战 二叉树 堆——纯C
“竹杖芒鞋轻胜马，谁怕？一蓑烟雨任平生”
猛戳订阅 纯C详解数据结构专栏
这里是目录
- 前言
- 堆的概念
- 创建结构体
- 初始化结构体
- 销毁结构体
- 向堆中插入数据
-
- 1.堆的物理结构和逻辑结构
- 2.完全二叉树下标规律
- 3.插入数据思路
- 依次打印堆的值
- 删除堆顶的值
- 判断堆是否为空
- 求堆中有几个元素
- 得到堆顶的值
- 堆排序
- 总体代码
-
- Heap.h
- Heap.c
- Test.c
前言
此篇详细实现二叉树中的一个顺序结构的实现——堆。并实现堆排序
重点是堆的规律和堆的实现
堆的概念
堆：将一些元素按完全二叉树的顺序存储方式存储在一个一维数组中。这就是堆。
完全二叉树：通俗讲就是只有最后一层的节点可以满，也可以不满。但是最后一层之前的节点要满，这就叫做完全二叉树。
小堆大堆：将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。（必须满足堆的性质）
堆的性质：
1.堆中某个节点的值总是不大于或不小于其父节点的值
2.堆总是一棵完全二叉树。
注意：
1.普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。
2.现实中我们通常把堆(一种特殊的二叉树)使用顺序结构的数组来存储。
3.需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。
接下来我们用纯C实现小堆
创建结构体
因为完全二叉树更适合使用顺序结构存储。而堆就是完全二叉树，所以我们需要创建顺序表
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;//a指向只一个堆数组
size_t size;//记录堆的大小
size_t capacity;//堆的最大容量
}HP;
初始化结构体
这一步必须要有，相当于创建变量了。
//初始化结构体
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
销毁结构体
因为是动态版的顺序表，有动态开辟就需要动态内存释放，也就是free掉a所指向的空间。
//销毁结构体
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
//free掉及时置空，防止野指针
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
向堆中插入数据
在插入数据之前，我们需要先知道堆的一个技巧。
1.堆的物理结构和逻辑结构
前面的步骤打造了一个堆的轮廓，你说它是堆吧，其实本质就是一个物理结构在内存中连续的顺序表罢了。也就是数组。如图下标从0开始。
但是要用到它的逻辑结构，需要把它想象成一个完全二叉树，就是下面图片这个样子。
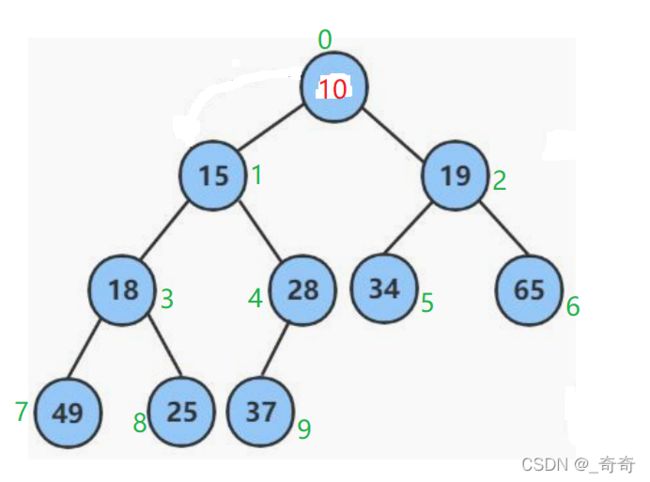
好了，现在我们要向堆中插入数据了，因为顺序表尾插效率高O(1),且尾插不会大幅度改变堆的结构。所以插入数据指的是尾插。
2.完全二叉树下标规律
注意：
1.尾插注意的是size的大小，size一直指向的是即将插入的那个空间。
2.和顺序表唯一不同的是尾插后需要向上调整数据，保持小堆的从上往下依次增大的结构
3.堆中的下标是有规律的。规律公式如下
这里需要强调的是对于父亲下标的计算。父亲的下标计算公式为：parent = (child - 1) / 2;
举个例子。因为假如左子树是7，右子树是8。7-1初以2是3, 但8-1初以2是3.5。但是计算机计算的结果也是3。
结论：所以管他是左子树，还是右子树，都能计算出其父亲的下标。
3.插入数据思路
最重要的思路是向上调整思想
我们以向堆中插入一个8为例。
因为size指向的是顺序表中即将插入的位置，所以直接插入就好了，但要及时让size++。
注意：尾插后size还需要指向下一个即将插入的位置。如图
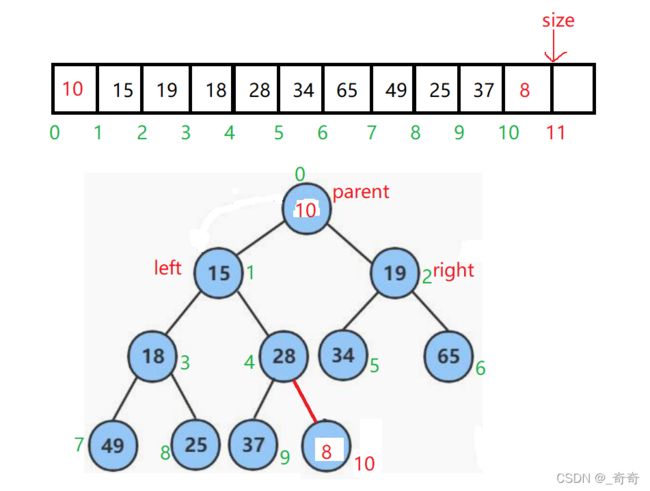然后开始向上调整8的位置。
思路：
1.让child依次和其parent比较，假如child小的话就交换两者的数据，使child的值依次向上走。然后迭代执行child = parent;parent = (child - 1) / 2;用来迭代parent和child的位置，直到child等于0。结束循环。
2.我觉得思路不难，难在把思路转换为代码然后实现。
3.注意实参传递的实参分别是数组首元素的地址，和新插入元素的下标。
//交换
void HeapSwap(HPDataType* pa, HPDataType* pb)
{
HPDataType tmp = *pa;
*pa = *pb;
*pb = tmp;
}
//向上调整
void AdjustUp(HPDataType* a, size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
//因为需要多次用到交换算法，所以写成一个函数，方便调用。
HeapSwap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//插入堆
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//除了AdjustUp
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
//注意realloc的用法
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)* newcapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
++php->size;
//唯一不同于顺序表的地方，向上调整算法
AdjustUp(php->a, php->size - 1);
}
依次打印堆的值
插入堆后，为了可视化，我们还是打印一下看看效果。
void HeapPrint(HP* php)
{
assert(php);
for (size_t i = 0; i < php->size; ++i)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
删除堆顶的值
删除也是一门艺术。今天的我是站在巨人的肩膀上学习堆的删除。
大佬们的算法思路是：
1.先让堆顶的值和堆尾的值交换O(1)，然后删除O(1)交换后堆尾的值。
2.再使用向下调整O(logN)算法，先比较left和right哪个小，谁小就让parent和谁交换，然后依次迭代，使堆顶的值向下调整。直到child大于size结束循环。
因为这样的时间复杂度是相当牛的。
注意：这里有几个地方代码技巧非常绝。
1.假设左子树就是最小的值。然后比较左右子树的大小后进行调整到底谁是最小的就OK了。这是非常的绝。因为你需要关注到底是左子树小还是右子树小！
//非常绝的一个思路
if (child+1 < size &&
a[child + 1] < a[child])
{
++child;
}
删除代码如下。
//向下调整
AdjustDown(HPDataType* a,size_t size, size_t root)
{
size_t parent= root;
size_t child= parent * 2 + 1;
while (child < size)
{
//判断哪个孩子小。
if (child+1 < size && a[child + 1] < a[child])
{
++child;
}
//交换父亲和孩子的值
if (a[child] < a[parent])
{
HeapSwap(&a[parent], &a[child]);
//迭代
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//删除堆顶的值
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
//交换堆顶和堆尾的值。然后删除堆尾的值
HeapSwap(php->a, &php->a[php->size - 1]);
--php->size;
//向下调整
AdjustDown(php->a, php->size, 0);
}
判断堆是否为空
当size为0时，堆即为空。
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
求堆中有几个元素
size标记的就是有几个元素。
//求堆中有几个元素
size_t HeapSize(HP* php)
{
assert(php);
return php->size;
}
得到堆顶的值
需要注意的是size最少为1.当size为0时，就意味着堆已经为空。所以我们需要assert断言size不为0.
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
堆排序
堆排序即利用堆的思想来进行排序，总共分为两个步骤：
- 建堆
升序：建大堆
降序：建小堆（我们这里用的是建小堆） - 利用堆删除思想来进行排序
void HeapSort(HPDataType* a, int size)
{
HP hp;
HeapInit(&hp);
//先创建一个小堆
for (int i = 0; i < size; i++)
{
HeapPush(&hp, a[i]);
}
size_t j = 0;
//利用堆删除思想来进行排序
while (!HeapEmpty(&hp))
{
a[j] = HeapTop(&hp);
j++;
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main()
{
//对a数组进行排序
int a[] = { 4,2,7,8,5,1,0,6 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
时间复杂度分析：
时间复杂度为O(N*logN)。比冒泡排序上升了一个档次哦。
但是空间复杂度有待改进。
但是空间复杂度因为占用了一个数组所以是O(N)。
空间复杂度改进的话需要很多字来详解。下篇博文继续叙述。
总体代码
Heap.h
#define _CRT_SECURE_NO_WARNINGS
#pragma once
#include Heap.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
//初始化结构体
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
//销毁结构体
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
//交换
void HeapSwap(HPDataType* pa, HPDataType* pb)
{
HPDataType tmp = *pa;
*pa = *pb;
*pb = tmp;
}
//向上调整
void AdjustUp(HPDataType* a, size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
HeapSwap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//插入堆
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)* newcapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
++php->size;
//向上调整
AdjustUp(php->a, php->size - 1);
}
//向下调整
AdjustDown(HPDataType* a,size_t size, size_t root)
{
size_t parent= root;
size_t child= parent * 2 + 1;
while (child < size)
{
if (child+1 < size && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
HeapSwap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//删除堆的值
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
//交换堆顶和堆尾的值。然后删除堆尾的值
HeapSwap(php->a, &php->a[php->size - 1]);
--php->size;
//向下调整
AdjustDown(php->a, php->size, 0);
}
//打印堆
void HeapPrint(HP* php)
{
assert(php);
for (size_t i = 0; i < php->size; ++i)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
//判断堆是否为空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
//求堆中有几个元素
size_t HeapSize(HP* php)
{
assert(php);
return php->size;
}
//得到堆顶的值
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
Test.c
#define _CRT_SECURE_NO_WARNINGS
#include "Heap.h"
void testHeap()
{
HP hp;
HeapInit(&hp);
HeapPush(&hp, 5);
HeapPush(&hp, 4);
HeapPush(&hp, 3);
HeapPush(&hp, 2);
HeapPush(&hp, 1);
HeapPrint(&hp);
/*HeapPop(&hp);
HeapPrint(&hp);*/
HeapDestroy(&hp);
}
void HeapSort(HPDataType* a, int size)
{
HP hp;
HeapInit(&hp);
for (int i = 0; i < size; i++)
{
HeapPush(&hp, a[i]);
}
size_t j = 0;
while (!HeapEmpty(&hp))
{
a[j] = HeapTop(&hp);
j++;
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main()
{
/*testHeap();*/
int a[] = { 4,2,7,8,5,1,0,6 };
HeapSort(a, sizeof(a) / sizeof(int));
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}