2021第十二届蓝桥杯Python组国赛/决赛 题解
2021第十二届蓝桥杯Python组国赛/决赛 题解
前言
2021年第十二届蓝桥杯国赛/决赛,因为疫情原因没有像往年一样前往北京参赛,而是在自己学校的机房进行考试,形式上类似蓝桥杯省赛,但由于参加国赛的都是在省赛上获得省一的同学,所以人数相对较少,换到了一个较小的机房统一考试,而这间机房正好就在我实验室隔壁,早上不用站在考场外干等了。
这届蓝桥杯也是本人第一次参加编程竞赛,之前无任何经验,这段时间通过把蓝桥杯省赛、国赛作为一个阶段性目标,让自己的代码水平比平时划水时提高了不少,这里不敢说自己算法水平有多大的提高,因为蓝桥杯和一些专业的编程赛事相比,还是有一些差距的。
由于我写这篇博客的时候,网上还找不到Python组的真题,所以就从其他组别的真题中找相同的题目先作题解了。
试题A 带宽

签到题,但我不会,往年省赛是考过这样的单位转换题的,考试时想着 b 和 B 之间好像是差一个 8倍的关系,结果答了个 200 * 8 = 1600。
正确答案应该是 200 // 8 = 25.
试题B 纯质数

本题也算签到题,我在考场上的想法就是直接对每个数分别判断:
1)是否为质数。
2)是否为纯质数。
判断是否为质数我觉得参加国赛的同学应该都能写对,但之后判断是否为纯质数就要注意不要漏数字了。
根据题意,一个数的某个数位上一旦出现质数,则该数就不是纯质数,那么数位上可能出现的质数应该是 0, 1, 4, 6, 8, 9,我自己在做的时候就漏掉了 0 。
代码如下:
其中判断质数的函数写法,我在之前写过的几篇省赛题解博客中有过详细介绍,感兴趣或者这里看不太明白的同学可以查看以前写的博客,主要思路围绕着“6的倍数”。
我们将关注点放在 6的倍数 上。任何一个数字对 6 取余,得到的余数都是在 0 ~ 5 之间,于是我们可以将任何一个数字表示为下列形式:
0)对6取余为0:6n
6的倍数,能被6整除,显然不是质数。
1)对6取余为1:6n + 1
2)对6取余为2:6n + 2
6n + 2 = 2 * (3n + 1),能被2整除,显然不是质数
3)对6取余为3:6n + 3
6n + 3 = 3 * (2n + 1),能被3整除,显然不是质数
4)对6取余为4:6n + 4
6n + 4 = 2 * (3n + 2),能被2整除,显然不是质数
5)对6取余为5:6n + 5
由此可见,只要一个数字对6取余的结果不为 1 或者 5 ,那么可以确定它一定不是质数。由此我们可以“剪枝”掉大量无用的计算。
那么对于那些余数为 1 或 5的数呢?它们就一定是质数吗?
答案是否定的,一个简单的反例是 24,24作为6的倍数,它的前后分别是 23 和 25,25作为余数为 1 的数字,却是质数,说明对于余数为 1 和 5 的数字,我们并不能确定它一定是质数,我们还需要对这些数单独进行判断。
代码中优化部分说的就是这部分,即对余数为 1 或 5 的数字单独判断是否为质数,那么我优化了什么呢?
正常判断一个数字是否为质数,我们需要从 2 开始遍历到该数的平方根,看是否能被整除,如果能被其中任意一个数除尽,则该数不是质数,若其中没有任意一个数能除尽,则该数为质数。
但仔细观察我们前面“剪枝”掉的数字,其中一部分是 2 * (3n + 1),即所有能被 2 整除的数字,也就是全部的偶数,全部的偶数都被我们“剪枝”掉了;同时 3 * (2n + 1) 说明我们同时也“剪枝”掉了全部能被 3 整除的数字。综上所述,我们可以跳过 2、3、4,从5开始尝试,并且跳过那些偶数进行判断,在Python中可以设置遍历步长为2来跳过那些偶数。这就是优化部分的思路。
最后这部分优化的思路,是在另一位Python组国赛选手ZBR同学的帮助下得出的,ZBR同学数学方面的思维在编程上带来了巨大的优势。
import math
# 判断一个数是否为质数
def is_prime(n):
if n == 1 or n == 4:
return False
if n == 2 or n == 3:
return True
if n % 6 == 1 or n % 6 == 5:
# 优化的地方
for i in range(5, int(math.sqrt(n) + 1), 2):
if n % i == 0:
return False
return True
else:
return False
# 判断一个数是否为纯质数
def is_pprime(n):
x = '014689'
for s in str(n):
if s in x:
return False
return True
res = 0
# 遍历题目范围中的每个数,依次判断质数与纯质数与否
for num in range(1, 20210605 + 1):
if is_pprime(num) and is_prime(num):
res += 1
print(res)
正确答案是 1903
顺带一提,如果忘记了 0 ,那么错误答案应该是5599或者5601之类的。
试题C 完全日期

本题我觉得也算签到题,至少因为我个人参加的是Python组,而Python处理日期有专门的datetime模块,非常的方便。
关键是要掌握两个点吧:
1)如何正确地遍历目标日期范围。
2)如何正确地判断一个日期是否为完全日期。
对于第一点,可以使用datetime模块中的datetime类和timedelta类完成。
对于第二点,可以解析出datetime类中的年月日信息进行求和处理。
说白了,本题只要你掌握了合适的API函数,基本就没啥坑点。
import datetime
import math
start = datetime.datetime(year=2001, month=1, day=1)
end = datetime.datetime(year=2021, month=12, day=31)
res = 0
for i in range(1, (end - start).days + 1):
cur = start + datetime.timedelta(days=i)
s = str(cur.year) + str(cur.month) + str(cur.day)
n = sum(list(map(int, s)))
if pow(int(math.sqrt(n)), 2) == n:
res += 1
print(res)
正确答案是977
试题D 最小权值

本题作为填空题的压轴,有一定的难度。考场上我先是观察了这个计算权重的式子,看能不能观察出一些端倪,然后我观察到,如果左子树或者右子树的节点数为0,那么该权重计算式就可以简化成这样:

此时考场上的我喜出望外,对于这样两种情况,显然选择前面系数为2的第二种情况,即右子树节点为0,将全部节点集中在左子树,同时递归地进行相同的处理,这样就可以得到一棵这样的树:
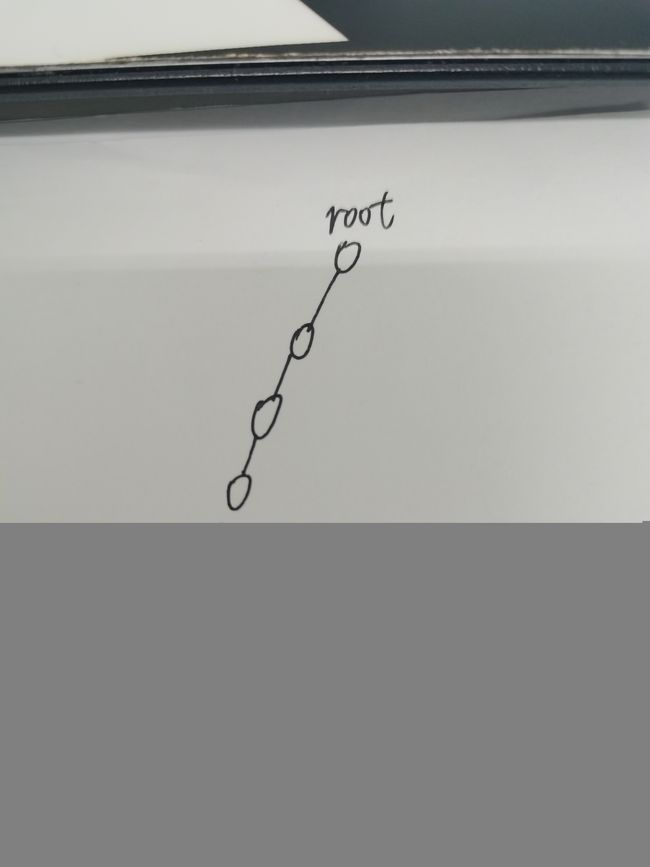
对于这样一棵树,我们转化后的权重计算式可以通过函数递归的形式进行计算,也就是这样:
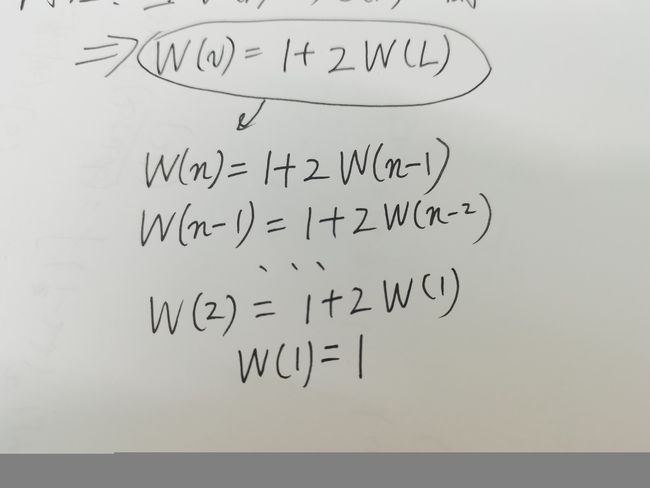
接着就是用代码来实现了:
def f(n):
if n == 1:
return 1
return 1 + 2 * f(n - 1)
print(f(2021))
结果一运行,发现栈溢出。没错,这就是Python不擅长递归的体现,Python递归的栈有限,一旦超出默认栈深度,就会抛出异常。
于是我在考场上是这样想的,我们递归个100次,然后把前100次递归的结果记录一下,接着跑 101次 - 200次递归,依次记录结果,直到 2021次都完成。虽然方法笨了点,但好歹不是无法解决的问题!
就在我兴高采烈地跑 f(100)的时候,却给出了这样的答案:
print(f(100))
# 1267650600228229401496703205375
没错,这个数字好像有点大啊,而且这才递归了100次,我们要递归2021次才行啊。我本能地反应过来,哦,我应该是忘记设置mod,结果应该是要对mod取余的吧,结果一看题目,本题根本没有要求对某个数取余。
这个时候警觉的我意识到,答案应该不可能这么大,代码逻辑非常简单,不可能写错,所以问题出在我的思路上,也就是我把全部结点集中在左子树上这个想法很可能是错的!一切都要推翻重新思考!
之后思考了一段时候无果,我就先去做后面的题目了,等回过头来再看本题时,一个念头油然而生,今年这一套题做下来,怎么一道动态规划的题目都没有啊,没错,动态规划是蓝桥杯非常爱出的一种题型,考前本人花了大功夫准备动态规划的,可是大题里全连一道DP题都没有。这一点让我萌生了,是否可以试着用DP的思路来解本题呢?
首先DP的第一步,定义状态,dp[i] 表示节点数为 i 的树的最小权重。
第二步,设计状态转移方程。对于 dp[i],树本身的根节点需要占用一个节点,因此剩余的 i - 1个节点要被左树和右树分配,左树分配 left 个节点,left 的取值范围是 0 ~ i - 1,那么右树可以被分配 right 个节点,right = i - 1 - left。
再结合题目给出的权重计算公式,那么得到状态转移方程为

第三步,设置DP数组的初值,显然根据题意有
dp[0] = 0,dp[1] = 1
代码如下:
dp = [float('inf') for _ in range(2021 + 1)]
dp[0], dp[1] = 0, 1
for i in range(2, 2021 + 1):
for left in range(i):
right = i - 1 - left
dp[i] = min(dp[i], 1 + 2 * dp[left] + 3 * dp[right] + left * left * right)
print(dp[-1])
答案是 2653631372
本题不保证答案的正确性,因为我也只是尝试着用DP去解题,无后效性和最优子结构之类的并没有通过证明去验证。
试题E 大写

本题是编程题中的签到题。对于Python,有现成的API函数可以使用,upper()函数可以将字符串中所有小写字母转化成大写字母,我觉得参加Python组国赛的同学应该能会用这个函数吧
print(input().upper())
生性多疑的我,在考场上不断阅读本题题干,试图找出该题隐藏的坑点,可惜无果,我记得给出的数据范围,保证了输入字符串长度是在100以内的。
考虑输入字符串的长度是因为,有些题因为输入字符串过长,会采用换行输入的方式,而一旦换行,对于Python input()函数就不那么友好了,我们就需要提前获取目标字符串长度,然后不断重复接受直到长度符合要求为止。这一点是我在洛谷等OJ上做题经常遇到的情况,但是对于本题应该不会发生,因为数据范围非常小。
试题F 123
本题我自己写得实在不太好。直接上ZBR同学的代码,应该是可以AC本题拿满分的代码
import math
# 求1-N的和
def getSum(n):
return (n*n+n)//2
# 求前N个数列 [1] , [1,2] , [1,2,3] , [1,2,3,4], ... , [1,2,3,...,N] 的所有数字之和 即对(n^2+n)/2求和
def getSum2(n):
return (n**3 + 3 * n*n + 2 * n) // 6
# 求第N个数在123数列中第几个数列的第几个 求解二次方程 (x^2+x)/2<=N
def findPosition(n):
if n == 0:
return (0, 0)
m = math.floor((math.sqrt(8*n + 1)-1) / 2)
c = (m*m+m) // 2
if n == c:
return (m, m)
else:
return (m + 1, n - c )
T = int(input())
# 策略是前N项数字和减去前M-1项数字的和
for i in range(T):
[M, N] = list(map(int, input().split()))
(M1, M2) = findPosition(M-1) # 计算得到第M-1个数字在第M1个数列的第M2项
(N1, N2) = findPosition(N) # 计算得到第N个数字在第N1个数列的第N2项
print(getSum2(N1-1) + getSum(N2) - getSum2(M1-1) - getSum(M2))
试题G 冰山
本题没有什么好的办法,就用模拟的方式写了,其实也就是暴力法吧
n, m, k = list(map(int, input().split()))
nums = list(map(int, input().split()))
for _ in range(m):
x, y = list(map(int, input().split()))
temp = []
i = 0
while i < len(nums):
nums[i] += x
if nums[i] > k:
temp.extend([1] * (nums[i] - k))
nums[i] = k
i += 1
elif nums[i] <= 0:
nums.pop(i)
else:
i += 1
nums.extend(temp)
nums.append(y)
print(sum(nums))
试题H 和与乘积

本题考察的点,说白了就是求区间和 以及 区间积,由于本人考前对于动态规划的准备比较多,而动态规划中有一部分就是专门讲得前缀和,当我们用O(N)的空间预处理出一个前缀和数组后,就可以在O(1)的时间内去得到一个区间内数字的和,前缀和的想法源自于重复计算结果的记忆化存储,例如,当我们想求区间 [1, 3] 和区间 [2, 5] 的数字和时,重复区间 [2, 3] 就被我们求了两次,这就是无用的重复计算,通过事先将可能的每个中间结果存储在前缀和数组中,我们每次就都可以迅速获得目标区间的区间和。
同理,前缀积就是前缀和的一个变种,同样可以在O(1)时间内获得目标区间的区间积。两者都是基于牺牲空间换取时间的思想。
另外一个可以使用前缀和 以及前缀积的点在于,本题的数组元素不会发生改变,所以前缀和前缀积数组一旦维护出来也不会改变,只要不断遍历就可以得到答案。
另外还有一点值得注意,就是前缀积数组存储的积,在数据量较大的情况下,可能会非常的大,ZBR同学就在考完后和我说过,他在做这题时,想到求积一定会爆int,所以采用了别的方式处理,但是其实Python的int类型理论上是可以存储无限大的整数,是不需要担心爆int 问题的。
n = int(input())
nums = list(map(int, input().split()))
sums, prod = [0], [1]
for num in nums:
sums.append(sums[-1] + num)
prod.append(prod[-1] * num)
res = 0
for left in range(n + 1):
for right in range(left, n + 1):
if sums[right] - sums[left - 1] == prod[right] // prod[left - 1]:
res += 1
print(res)
为了验证前缀和的性能,我和ZBR同学讨论用Python random模块去生成2W ~ 20W以内的测试用例,结果发现随便一个5W规模的测试用例都无法在5s内跑完,事实上它一直在跑,就没出答案过,所以我觉得这段代码一定不能AC,但可以拿一部分分数。
试题I 二进制问题

本题可以用暴力法得一些分,也可以用排列组合去骗一些分,但是骗分有风险,骗分需谨慎。
n, k = list(map(int, input().split()))
res = 0
for num in range(1, n + 1):
if bin(num).count('1') == k:
res += 1
print(res)
另一个骗分写法是这样的,我们先求出 边界数N 的二进制位数c,然后题目就转换为在 c 位数字中取 k 个位置放1 有多少种组合,也就是组合数(c, k)。
之所以说是骗分,是因为很可能相同二进制位数中,那些大于 N 的数字也是可行解,所以该方法只能碰运气。
本题只用暴力法的话,大多数人应该都能写出来,所以才试着用这样骗分的方式碰运气,其实是考场上没考虑到 大于N但位数相同的情况,考完和ZBR同学讨论才意识到的。
# 骗分咯
from itertools import combinations
n, k = list(map(int, input().split()))
c = len(bin(n)) - 2
comb = combinations(range(c), k)
print(len(list(comb)))
试题J 翻转括号序列


本题是标准的括号序列匹配问题,吧。对于题目中的操作1,我个人在考场上觉得应该是没有什么好的办法去优化的,只能一个个字符老老实实地去翻转(修改)。而操作2才是真正值得想办法解决的问题。
我本人在学习栈这种数据结构时记得,栈的应用中,对于表达式匹配问题就有天然的优势,也就是说我们可以通过栈这种数据结构去验证一个括号序列是否合法。具体方式如下:
1)初始时,栈为空,我们依次遍历括号序列中的每一个字符
2)若当前栈为空,或当前遍历到的字符是 左括号,则将该左括号入栈
3)若当前栈顶元素为左括号(这里隐含了栈非空),且当前遍历到的字符是右括号,则发生匹配,我们将栈顶元素出栈。
4)遍历完整个括号序列后,若栈为空,说明全部字符都被匹配掉了,若栈中还有元素剩余,则说明该序列不合法。
基于这一点,我们可以考虑本题,从给定的 L 开始遍历括号序列,采用上述的出入栈策略,当某个时刻(除了初始时刻),栈为空,说明目前为止的序列都是合法的,我们此时记录一下当前的下标,作为R,那么 [L , R]就是一段合法的括号序列。
直到遍历到括号序列末端,记录下最远的R就是我们的答案。
n, m = list(map(int, input().split()))
nums = list(input())
print(nums)
for _ in range(m):
a, *b = list(map(int, input().split()))
if a == 1:
left, right = b[0], b[1]
for i in range(left, right + 1):
nums[i] = '(' if nums[i] == ')' else ')'
else:
start = b[0] - 1
i = start
res = start
stack = []
for i in range(start, n):
if nums[i] == '(':
stack.append('(')
else:
if not stack:
break
elif stack[-1] == '(':
stack.pop()
if not stack:
res = i
print(res + 1 if res != start else 0)
总结
总结一下,本次蓝桥杯是我第一次参加编程竞赛,也可能是最后一次,省赛一度以为自己没了,但还是以全省第三的名次进了省一,相反国赛的难度让我觉得一般,但出来以后发现考试结果可能并没有那么好,我绝不是那种看到题目简单就大意粗心的人,只能说没发挥好吧,很多地方不该出错的都出错了,编程大题很难拿到高分,在这种情况下第一第二个填空题都错了,丢了10分,以至于国一的目标很可能达不到,顺带一提,看贴吧里的反映,好像周三也就是6.9出国赛成绩,希望能让我拿个奖就好吧。这段时间也算是通过蓝桥杯这个阶段性目标,好好复习准备了一下算法,不至于说整天浑水摸鱼了。
最后,虽然自己没啥经验,但是通过本次国赛还是能给出一点经验,注重基础,务必把简单题签到题的分那满了,编程大题不说样例分吧,至少暴力解法要能写出来,然后尽可能优化自己的暴力解法,能剪枝的地方务必剪枝,如果能用上一些稍微好点的数据结构和算法,那再往上面去写。对于蓝桥杯来说,能拿到这些分数,省赛省一肯定是没问题的,国赛能拿什么名次,我就不知道了。
基础很重要、基础很重要、基础很重要。