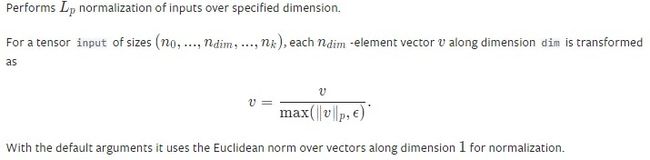【Pytorch】常见的人脸身份识别损失函数
【Pytorch】常见的人脸身份识别损失函数
实验环境准备:人脸多角度多光照的图像数据集MUCT(276个受试者)+ MobileNetV3
文章目录
-
- 【Pytorch】常见的人脸身份识别损失函数
-
- 0、Softmax(激活函数)
- 1、NLLLoss(负对数似然损失)
-
- 1)源码解析
- 2)实验
- 2、CrossEntropyLoss(损失函数)
-
- 1)源码解析
- 2)实验
- 3、Center loss(损失函数 - 2016)
-
- 1)源码解析
- 2)实验
- 4、L2-Softmax(损失约束 - 2017 特征归一化)
-
- 1)源码
- 2)实验
- 5、SphereFace loss(损失约束 - 2017 权重归一化)
-
- 1)源码
- 2)实验
- 6、cosFace Loss(损失约束 - 2018 特征权重归一化)
-
- 1)源码
- 2)实验
- 7、ArcFace loss(损失约束 - 2018 特征权重归一化)
-
- 1)源码解析
- 2)实验
- 3)ArcFace Loss为Nan怎么解决
- 8、参考源码
0、Softmax(激活函数)
参考TORCH.NN.FUNCTIONAL.SOFTMAX
为了区分下面提到的softmax loss(也就是多分类的交叉熵损失函数),以及L2-softmax loss,ArcFace loss,cosFace loss等,这里有必要先提一下Softmax激活函数。Softmax激活函数如下:
S o f t m a x ( x i ) = e x p ( x i ) ∑ j = 1 e x p ( x j ) Softmax(x_i) = \frac{exp(x_i)}{\sum_{j = 1}exp(x_j)} Softmax(xi)=∑j=1exp(xj)exp(xi)
该函数的目的是将input中的每个元素缩放至[0,1]区间上(归一化),且各元素之和为1,且输出向量的维数和输入向量的维数保持不变。
而对于Softmax损失函数式子如下,只不过下面的 w x + b wx + b wx+b是全连接层(nn.Linear(inputSize,outputSize)) 的输出;而取对数的作用其实是将Softmax归一化结果进行再次变换,用于表示 x i + 1 x_{i + 1} xi+1(线性变换后的特征可用于分类任务)属于各个类别 { y 1 , . . . , y n } \{y_1,...,y_n\} {y1,...,yn}的概率; m m m表示mini-batch的大小,求和的目的是计算当前批量任务的总损失值。
L S = − ∑ i = 1 m l o g e W y i T x i + b y i ∑ j = 1 n e W j T x i + b j = − ∑ i = 1 m l o g S o f t m a x ( x i ) L_S = - \sum_{i = 1}^m log\frac{e^{W^T_{y_i}x_i + b_{yi}}}{\sum_{j=1}^ne^{W^T_jx_i + b_j}} = - \sum_{i = 1}^m log Softmax(x_i) LS=−i=1∑mlog∑j=1neWjTxi+bjeWyiTxi+byi=−i=1∑mlog Softmax(xi)
L S L_S LS损失函数其实就是下面提到的CrossEntropyLoss,用于多分类的交叉熵损失函数。
Note:全连接层的输出结果才可用于Softmax归一化
假设模型部分结构如下:
... self.linear3 = nn.Linear(960, 1280) self.bn3 = nn.BatchNorm1d(1280) self.hs3 = hswish() self.linear4 = nn.Linear(1280, num_classes = 276) #输出类别数为276假设batch_size为4,则最后一层全连接层的输入维数为: [ 4 , 1280 ] [4, 1280] [4,1280],输出维数为: [ 4 , 276 ] [4, 276] [4,276],该层权重 W W W维数为 [ 1280 , 276 ] [1280,276] [1280,276];其中 W W W中的每一列表示第 j j j个类别的权重向量。
接着代入上面的Softmax函数,即可实现对 W T X ∈ R [ 4 , 276 ] W^TX \in R[4,276] WTX∈R[4,276] 的线性变换后的特征进行归一化操作。
1、NLLLoss(负对数似然损失)
NLLLoss - Negative Log Likelihood Loss 参考NLLLOSS - pytorch
l ( x , y ) = L = { l 1 , . . . , l N } T , l n = − w y n x n , y n , w c = w e i g h t [ c ] ∗ 1 { c ≠ i g n o r e _ i n d e x } l(x,y) = L = \{l_1,...,l_N\}^T, l_n = -w_{y_n}x_{n,y_n},w_c = weight[c] * 1 \{c \neq ignore\_index\} l(x,y)=L={l1,...,lN}T,ln=−wynxn,yn,wc=weight[c]∗1{c=ignore_index}
其中 x x x是输入, y y y是目标输出, w w w是权重, N N N是batch size, C C C为类别数。
对于input和target(每个元素为类别标签),它有一定要求:
The input given through a forward call is expected to contain log-probabilities of each class. input has to be a Tensor of size either ( m i n i b a t c h , C ) (minibatch, C) (minibatch,C)or ( m i n i b a t c h , C , d 1 , d 2 , . . . , d K ) (minibatch, C, d_1, d_2, ..., d_K) (minibatch,C,d1,d2,...,dK) with K ≥ 1 K \geq 1 K≥1 for the K-dimensional case. The latter is useful for higher dimension inputs, such as computing NLL loss per-pixel for 2D images.
The target that this loss expects should be a class index in the range [ 0 , C − 1 ] [0, C-1] [0,C−1]where C = number of classes; if ignore_index is specified, this loss also accepts this class index (this index may not necessarily be in the class range).
- input维数为N x C,则target中每个元素的值要满足 0 <= value < C;
- input维数为N x C x height x width,则target中每个元素的值要满足 0 <= value < C
1)源码解析
import torch
import torch.nn as nn
#The negative log likelihood loss
#参考 https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html#torch.nn.NLLLoss
m = nn.LogSoftmax(dim=1) #logSoftmax = log(softmax) is an activation layer
loss = nn.NLLLoss()
# input is of size N x C = 3 x 5
# input = torch.randn(3, 5, requires_grad=True)
input = torch.tensor([[-1.0,-2.0,-3.0],[1.0,2.0,3.0],[5.0,7.0,3.0]],requires_grad=True)
# each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 2])
output = loss(m(input), target)
print(f"1: NLLLoss( logSoftmax(input) = {m(input)}, target = {target} ) = {output}")
print(f"torch.nn.functional.one_hot(target) * m(input) = {torch.nn.functional.one_hot(target) * m(input)}")
print(f"-torch.mean(torch.nn.functional.one_hot(target) * m(input)) * (input.shape[1]) = {-torch.mean(torch.nn.functional.one_hot(target) * m(input)) * (input.shape[1])}")
output.backward()
---
1: NLLLoss( logSoftmax(input) = tensor([[-0.4076, -1.4076, -2.4076],
[-2.4076, -1.4076, -0.4076],
[-2.1429, -0.1429, -4.1429]], grad_fn=<LogSoftmaxBackward>), target = tensor([1, 0, 2]) ) = 2.652714729309082
torch.nn.functional.one_hot(target) * m(input) = tensor([[-0.0000, -1.4076, -0.0000],
[-2.4076, -0.0000, -0.0000],
[-0.0000, -0.0000, -4.1429]], grad_fn=<MulBackward0>)
-torch.mean(torch.nn.functional.one_hot(target) * m(input)) * (input.shape[1]) = 2.652714729309082
你会发现,NLL_loss的计算原理如下:先对target进行one_hot编码,接着target和** l o g _ S o f t m a x ( i n p u t ) ∈ ( ∞ , 0 ] log\_Softmax(input) \in (\infty,0] log_Softmax(input)∈(∞,0]相乘**,得到的矩阵如下:
tensor([[-0.0000, -1.4076, -0.0000],
[-2.4076, -0.0000, -0.0000],
[-0.0000, -0.0000, -4.1429]]
再对各类别取平均(这里类别数为3),取负数得到最终的损失值:
-torch.mean(torch.nn.functional.one_hot(target) * m(input)) * (input.shape[1])
更多源码见官网 https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html#torch.nn.NLLLoss
2)实验
使用NLLLoss对MobileNetV3进行训练,简单修改如下:
class MobileNetV3_Large(nn.Module):
...
def forward(self, x):
#MobileNetV3_Large原来的模块
out = self.hs1(self.bn1(self.conv1(x)))
out = self.bneck(out)
out = self.hs2(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, 7)
out = out.view(out.size(0), -1)
out = self.hs3(self.bn3(self.linear3(out)))
out = self.linear4(out)
#新增模块
out = F.log_softmax(out) #无需保存参数,直接使用functional里的方法即可
return out
...
#接着在train.py中使用NLLLoss即可
out = model(sample)
loss = nll_loss(out,y) # 总损失: NLLLoss(log(softmax)) = crossEntropyLoss
检测效果如下:
Epoch 1/100: 100%|▉| 2800/2802 [01:24<00:00, 33.18 epoch = 0, train_loss = 22.36589876106807, train_acc = 0.0064285714285714285,test_loss = 7.780539038635435, test_acc = 0.001488095238095238 checkpoint1 is saved Epoch 2/100: 100%|▉| 2800/2802 [01:22<00:00, 33.85 epoch = 1, train_loss = 7.284130101885115, train_acc = 0.002142857142857143,test_loss = 6.771463133039928, test_acc = 0.00744047619047619 Epoch 3/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint2 is saved Epoch 3/100: 100%|▉| 2800/2802 [01:22<00:00, 34.05 epoch = 2, train_loss = 6.8465765258244105, train_acc = 0.005,test_loss = 6.706081149123964, test_acc = 0.00744047619047619 checkpoint3 is saved Epoch 4/100: 100%|▉| 2800/2802 [01:22<00:00, 34.03 epoch = 3, train_loss = 6.661047067642212, train_acc = 0.0032142857142857142,test_loss = 6.852347408022199, test_acc = 0.002976190476190476 Epoch 5/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint4 is saved Epoch 5/100: 100%|▉| 2800/2802 [01:22<00:00, 33.83 epoch = 4, train_loss = 6.594039328438895, train_acc = 0.002857142857142857,test_loss = 6.599982026077452, test_acc = 0.004464285714285714 ```
2、CrossEntropyLoss(损失函数)
参考CROSSENTROPYLOSS
l ( x , y ) = L = { l 1 , . . . , l N } T , l n = − w y n l o g e x p ( x n , y n ) ∑ c = 1 C e x p ( x n , c ) ⋅ 1 { y n ≠ i g n o r e _ i n d e x } l(x,y) = L = \{l_1,...,l_N\}^T,l_n = -w_{yn} log\frac{exp(x_{n,y_n})}{\sum_{c=1}^C exp(x_{n,c})} \cdot 1 \{y_n \neq ignore\_index\} l(x,y)=L={l1,...,lN}T,ln=−wynlog∑c=1Cexp(xn,c)exp(xn,yn)⋅1{yn=ignore_index}
The input is expected to contain raw, unnormalized scores for each class. input has to be a Tensor of size ( C ) (C) (C) for unbatched input, ( m i n i b a t c h , C ) (minibatch, C) (minibatch,C) or ( m i n i b a t c h , C , d 1 , d 2 , . . . , d K ) (minibatch, C, d_1, d_2, ..., d_K) (minibatch,C,d1,d2,...,dK) with K ≥ 1 K \geq 1 K≥1for the K-dimensional case. The last being useful for higher dimension inputs, such as computing cross entropy loss per-pixel for 2D images.
The target that this loss expects should be a class index in the range [ 0 , C − 1 ] [0, C-1] [0,C−1]where C = number of classes;
- input维数为N x C,则target中每个元素的值要满足 0 <= value < C;
- input维数为N x C x height x width,则target中每个元素的值要满足 0 <= value < C
1)源码解析
import torch
import torch.nn as nn
#参考 https://pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html#torch.nn.CrossEntropyLoss
# Example of target with class indices
loss = nn.CrossEntropyLoss()
# input = torch.randn(3, 5, requires_grad=True)
# target = torch.empty(3, dtype=torch.long).random_(5)
input = torch.tensor([[-1.0,-2.0,-3.0],[1.0,2.0,3.0],[5.0,7.0,3.0]],requires_grad=True)
# each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 2])
output = loss(input, target)
print(f"1: CrossEntropyLoss(input = {input}) = {output}")
output.backward()
---
1: CrossEntropyLoss(input = tensor([[-1., -2., -3.],
[ 1., 2., 3.],
[ 5., 7., 3.]], requires_grad=True)) = 2.652714729309082
你会发现,CrossEntropyLoss的计算结果与经过Softmax和取对数之后的NLLLoss计算结果一样。因此:
CrossEntropyLoss(out,y) = NLLLoss(log(softmax(x)),y)
2)实验
使用CrossEntropyLoss对MobileNetV3进行训练,简单修改如下:
#在train.py中使用NLLLoss即可
out = model(sample)
loss = cross_entropy_loss(out,y) # 总损失: NLLLoss(log(softmax)) = crossEntropyLoss
训练结果如下:
Epoch 1/100: 100%|▉| 2800/2802 [01:24<00:00, 33.26 epoch = 0, train_loss = 23.81213624749865, train_acc = 0.003928571428571429,test_loss = 7.5758026611237295, test_acc = 0.005952380952380952 Epoch 2/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint1 is saved Epoch 2/100: 100%|▉| 2800/2802 [01:22<00:00, 33.98 epoch = 1, train_loss = 7.077970628057208, train_acc = 0.0035714285714285713,test_loss = 6.91069389524914, test_acc = 0.002976190476190476 Epoch 3/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint2 is saved Epoch 3/100: 100%|▉| 2800/2802 [01:22<00:00, 33.86 epoch = 2, train_loss = 6.829764229910714, train_acc = 0.005,test_loss = 6.861410782450721, test_acc = 0.0 checkpoint3 is saved Epoch 4/100: 100%|▉| 2800/2802 [01:22<00:00, 33.89 epoch = 3, train_loss = 6.701256164142063, train_acc = 0.004642857142857143,test_loss = 6.797497911112649, test_acc = 0.001488095238095238 checkpoint4 is saved Epoch 5/100: 100%|▉| 2800/2802 [01:23<00:00, 33.72 epoch = 4, train_loss = 6.5600184038707186, train_acc = 0.004285714285714286,test_loss = 6.7159488428206675, test_acc = 0.001488095238095238 checkpoint5 is saved效果和NLLLoss一样的,只不过前者需要在MobileNetV3模型中添加一层log_softmax(不是模块),进行特征的缩放,而CrossEntropyLoss使用时无需修改模型层结构。
3、Center loss(损失函数 - 2016)
参考
- CenterLoss | 减小类间距离
- 损失函数改进之Center Loss
- Pytorch入门学习(八)-----自定义层的实现(甚至不可导operation的backward写法)
center loss的原理主要是在softmax loss的基础上,通过对训练集的每个类别在特征空间分别维护一个类中心,在训练过程,增加样本经过网络映射后在特征空间与类中心的距离约束,从而兼顾了类内聚合与类间分离。
最终通过将centerloss和softmax loss进行加权求和,实现整体的分类任务的学习。
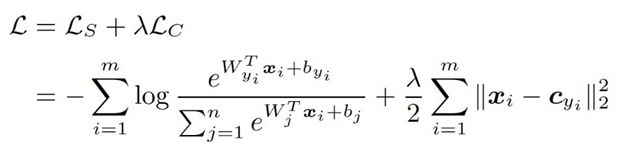
对于第二部分的center loss,
c y i c_{yi} cyi 表示第 y i yi yi个类别的特征中心(特征中心的维数和全连接之前的特征 x i x_{i} xi相同),主要通过初始化(反向更新)的center loss的中心参数,利用 y i y_i yi的索引获取指定的行的参数特征,用于计算特征和特征中心的距离。
x i x_i xi表示全连接层之前的特征,而全连接之后的特征 x i + 1 x_{i+1} xi+1用于计算softmax loss。
Centor loss算法流程如下:
1)源码解析
参考
- https://github.com/jxgu1016/MNIST_center_loss_pytorch/blob/master/MNIST_with_centerloss.py
- https://pytorch.org/docs/stable/notes/extending.html#extending-autograd
- pytroch中ctx和self的区别
class CenterLoss(nn.Module):
def __init__(self, num_classes, feat_dim, size_average=True):
super(CenterLoss, self).__init__()
self.centers = nn.Parameter(torch.randn(num_classes, feat_dim)) #Parameters are Tensor subclasses
self.centerlossfunc = CenterlossFunc.apply # pytorch中的model.apply(fn)会递归地将函数fn应用到父模块的每个子模块submodule,也包括model这个父模块自身
self.feat_dim = feat_dim
self.size_average = size_average
def forward(self, feat, label):
batch_size = feat.size(0)
feat = feat.view(batch_size, -1)
# To check the dim of centers and features
if feat.size(1) != self.feat_dim:
raise ValueError(
"Center's dim: {0} should be equal to input feature's dim: {1}".format(self.feat_dim, feat.size(1)))
loss = self.centerlossfunc(feat, label, self.centers) #通过输入特征,真实标签和特征中心正向传播计算损失
loss /= (batch_size if self.size_average else 1)
return loss
#https://pytorch.org/docs/stable/notes/extending.html#extending-autograd
class CenterlossFunc(Function):
@staticmethod
# ctx用在静态方法中, 调用的时候不需要实例化对象, 直接通过类名就可以调用, 所以self在静态方法中没有意义
#自定义的forward()方法和backward()方法的第一个参数必须是ctx; ctx可以保存forward()中的变量,以便在backward()中继续使用
def forward(ctx, feature, label, centers):
ctx.save_for_backward(feature, label, centers)
centers_batch = centers.index_select(0, label.long()) #等价于torch.index_select(centers, 0, label.long()),第二个参数0表示按行索引,1表示按列进行索引,第三个参数是一个tensor,就是索引的序号
return (feature - centers_batch).pow(2).sum() / 2.0
@staticmethod
def backward(ctx, grad_output):
feature, label, centers = ctx.saved_tensors
centers_batch = centers.index_select(0, label.long())
diff = centers_batch - feature
# init every iteration
counts = centers.new(centers.size(0)).fill_(1)
ones = centers.new(label.size(0)).fill_(1)
grad_centers = centers.new(centers.size()).fill_(0)
counts = counts.scatter_add_(0, label.long(), ones)
grad_centers.scatter_add_(0, label.unsqueeze(1).expand(feature.size()).long(), diff)
grad_centers = grad_centers / counts.view(-1, 1)
return - grad_output * diff, None, grad_centers
解释一下为什么要,以及什么时候要继承torch.autograd.function的Function模块:https://pytorch.org/docs/stable/notes/extending.html#extending-autograd
如果想给新添加的算子实现“autograd”自动求导的功能,则需要为每一个算子实现
Function子类。
- In general, implement a custom function(自定义方法) if you want to perform computations in your model that are not differentiable or rely on non-Pytorch libraries (e.g., NumPy), but still wish for your operation to chain with other ops and work with the autograd engine.
- In some situations, custom functions can also be used to improve performance and memory usage: If you implemented your forward and backward passes using a C++ extension, you can wrap them in
Functionto interface with the autograd engine. If you’d like to reduce the number of buffers saved for the backward pass, custom functions can be used to combine ops together.- If you can already write your function in terms of PyTorch’s built-in ops, its backward graph is (most likely) already able to be recorded by autograd. In this case, you do not need to implement the backward function yourself. Consider using a plain old Python function.
就是说如果我们想通过Numpy库(而非Pytorch库)来实现某个功能算子,又想将自定义的算子和其他算子进行链式绑定实现自动求导,此时则需要继承
torch.autograd.function.Function,通过底层的C++扩展包来实现forward,backward前向和反向传播的方法。 如果我们使用pytorch构建的算子来自定义方法,则此时的计算图会在正向传播时,通过自动求导将计算图的拓扑结构进行保存。
具体的函数(
save_for_backward(),mark_dirty()等)介绍参考官网
2)实验
使用CenterLoss对MobileNetV3进行训练,简单修改如下:
class MobileNetV3_Large(nn.Module):
...
def forward(self, x):
out = self.hs1(self.bn1(self.conv1(x)))
out = self.bneck(out)
out = self.hs2(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, 7)
out = out.view(out.size(0), -1)
out = self.hs3(self.bn3(self.linear3(out)))
out1 = out #输出特征,用于计算centerloss
out2 = self.linear4(out) #用于计算softmax loss(return2)
return out1,out2
...
#接着在train.py中使用NLLLoss即可
softmax_loss = nn.CrossEntropyLoss().to(device) # NLLLoss
Center_Loss = CenterLoss(num_classes=num_classes,feat_dim=1280).to(device) #center_loss
weight = 0.3 #总损失: NLLLoss + center_loss * weight
for epoch in range(0,epoches):
feat,predict = model(sample)
#参考 https://github.com/jxgu1016/MNIST_center_loss_pytorch/blob/master/MNIST_with_centerloss.py
loss = softmax_loss(predict,y) + weight * Center_Loss(feat,y) # 总损失: NLLLoss + center_loss * weight
效果如下:
epoch = 44, train_loss = 197.36729516165596, train_acc = 0.002142857142857143,test_loss = 821.500404267084, test_acc = 0.005952380952380952
checkpoint45 is saved
Epoch 46/100: 100%|▉| 2800/2802 [01:25<00:00, 32.8
epoch = 45, train_loss = 197.30666959490094, train_acc = 0.004642857142857143,test_loss = 2388.358141308739, test_acc = 0.005952380952380952
Epoch 47/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint46 is saved
Epoch 47/100: 100%|▉| 2800/2802 [01:26<00:00, 32.4
epoch = 46, train_loss = 197.23798839024136, train_acc = 0.004642857142857143,test_loss = 80160891858.68933, test_acc = 0.005952380952380952
Epoch 48/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint47 is saved
Epoch 48/100: 100%|▉| 2800/2802 [01:25<00:00, 32.5
epoch = 47, train_loss = 197.2484938921247, train_acc = 0.0032142857142857142,test_loss = 1961.587382089524, test_acc = 0.004464285714285714
Epoch 49/100: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint48 is saved
Epoch 49/100: 100%|▉| 2800/2802 [01:25<00:00, 32.7
epoch = 48, train_loss = 197.18114281790596, train_acc = 0.005,test_loss = 2588.5203427814304, test_acc = 0.005952380952380952
checkpoint49 is saved
Epoch 50/100: 100%|▉| 2800/2802 [01:28<00:00, 31.5
epoch = 49, train_loss = 197.15495856148857, train_acc = 0.0035714285714285713,test_loss = 39041072659.06345, test_acc = 0.005952380952380952
checkpoint50 is saved
在使用MUCT数据集时,发现loss值一直降不下来
4、L2-Softmax(损失约束 - 2017 特征归一化)
参考
- L2_Softmax Loss
关于L2约束的Softmax loss出现的背景
人脸验证在LFW数据集上做的很好,但是在实际场景:存在大量视角、分辨率、图像质量变化和遮挡时,验证效果并没有那么理想。主要是两个原因造成的:
- 1.数据质量不均衡:目前常用的人脸识别公开训练集图像大都是高清、正脸人脸图像,很少包含无限制条件下的难以识别的人脸图像。现在大多数的DCNN模型,使用softmax loss做分类,使用前面提到的训练集训练出来的模型,对高质量的图像过拟合,但对难以识别的图像欠拟合。
- 2.softmax loss不适合做人脸验证任务:softmax loss只是保证学习到的特征不用做任何matric learning的时候,能够使得人脸特征可分。但是softmax loss并没有保证positive pairs学到的特征足够近而negative pairs学到的特征足够远,因此不是很适合去做人脸验证任务。另外一点是,softmax loss是要最大化给定的mini-batch中所有样本的条件概率。但是,由于高质量的人脸图像的特征范数较大,低质量人脸图像的特征范数较小,如果直接让容易验证的样本的范数比较大,让难以验证的样本的范数较小,则可以得到最小化的softmax loss。因此,如果直接使用softmax loss只关注了mini-batch中高质量的人脸图像,而忽略了该mini-batch中较少的低质量的人脸图像。
解决方法:
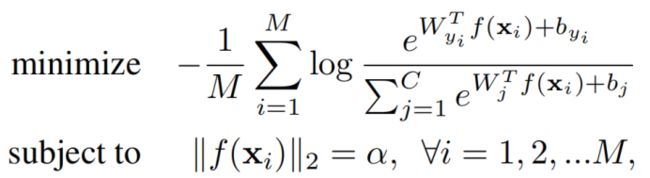
在满足关于 f ( x i ) f(x_i) f(xi)特征归一化到固定值 α \alpha α的约束下,最小化softmax loss。其中 f ( x i ) f(x_i) f(xi)是DCNN倒数第二层提取到的特征。
参数α有两种设置方式,一是在训练过程中设置α为固定值,二是通过训练获得。但是第二种方式得到的α会得到比较大的值,添加的限制太过宽松。作者建议设置为一个比较小的固定值。
作者也观察到α的值设置太小的时候,超球面的表面积太小,特征分布不开,最后验证准确率也不高。
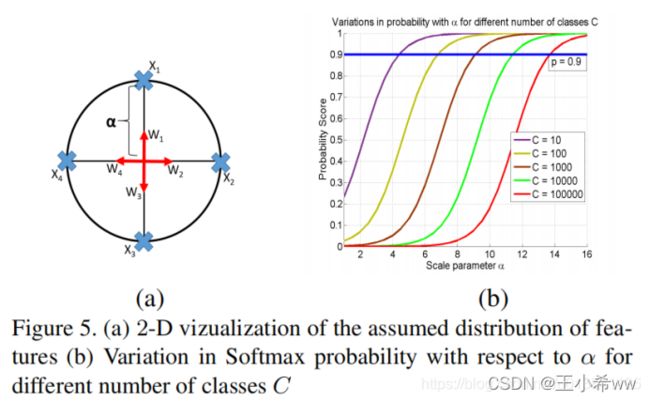
上图(b)表示以验证准确率p=0.9时,类别数C越大,需要的 α \alpha α值越大。
作者建议的 α \alpha α最小值为:
α l o w = l o g p ( C − 2 ) 1 − p \alpha_{low} = log \frac{p(C - 2)}{1 - p} αlow=log1−pp(C−2)
实现细节就是增加一个L2归一化层,进行特征的缩放处理,最后再乘上 α \alpha α
这里可以使用
F.normalize来计算 L p L_p Lp范数 。参考 https://pytorch.org/docs/stable/generated/torch.nn.functional.normalize.html?highlight=normalize#torch.nn.functional.normalize
- 由于损失函数使得所有人脸图像的特征的范数大小相同,所以softmax loss不会只偏重于对easy samples的学习,也会对diffcult samples进行学习;
- 还是由于特征的范数大小一致,所以所有的特征样本的特征都分布于一个固定半径的超球面上,此时最小化softmax loss等价于最大化positive pairs之间的余弦相似度,同时最小化negative pairs之间的余弦相似度。
简单来说,就是由于softmax loss在图片分类的优化过程中,仅关注特征范数大的高质量的图片,忽略了范数低的图片,为了解决图片质量对模型的训练效果的问题,提出要归一化特征,使得模型学到的特征既能够关注高质量的图片,也能够关注低质量的图片。
1)源码
#L2归一化层
class NormLinear(nn.Module):
def __init__(self, in_features, classes, weight_norm=False, feature_norm=False):
super(NormLinear, self).__init__()
self.weight_norm = weight_norm
self.feature_norm = feature_norm
self.classes = classes
self.in_features = in_features
self.weight = nn.Parameter(torch.Tensor(classes, in_features))
nn.init.normal_(self.weight, std=0.01)
def forward(self, x):
weight = F.normalize(self.weight, 2, dim=-1) if self.weight_norm else self.weight
if self.feature_norm:
x = F.normalize(x, 2, dim=-1)
return F.linear(x, weight)
def extra_repr(self):
return 'in_features={}, out_features={}'.format(self.in_features, self.classes)
class L2Softmax(nn.Module):
r"""L2Softmax from
`"L2-constrained Softmax Loss for Discriminative Face Verification"
`_ paper.
Parameters
----------
classes: int.
Number of classes.
alpha: float.
The scaling parameter, a hypersphere with small alpha
will limit surface area for embedding features.
p: float, default is 0.9.
The expected average softmax probability for correctly
classifying a feature.
from_normx: bool, default is False.
Whether input has already been normalized.
Outputs:
- **loss**: loss tensor with shape (1,). Dimensions other than
batch_axis are averaged out.
"""
def __init__(self, embedding_size, classes, alpha=64, p=0.9):
super(L2Softmax, self).__init__()
alpha_low = math.log(p * (classes - 2) / (1 - p))
assert alpha > alpha_low, "For given probability of p={}, alpha should higher than {}.".format(p, alpha_low)
self.alpha = alpha
self.linear = NormLinear(embedding_size, classes, True, True)
def forward(self, x, target):
x = self.linear(x)
x = x * self.alpha
return x
2)实验
使用L2-softmax对MobileNetV3进行训练,简单修改如下:
class MobileNetV3_Large(nn.Module):
def __init__(self, num_classes=1000):
...
self.linear4 = nn.Linear(1280, num_classes)
self.l2_softmax = L2Softmax(embedding_size=num_classes,classes=num_classes)
def forward(self, x):
out = self.hs1(self.bn1(self.conv1(x)))
out = self.bneck(out)
out = self.hs2(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, 7)
out = out.view(out.size(0), -1)
out = self.hs3(self.bn3(self.linear3(out)))
out = self.linear4(out)
out = self.l2_softmax(out,None) #使用L2归一化 * α来处理特征
return out
...
#接着在train.py中使用NLLLoss即可
softmax_loss = nn.CrossEntropyLoss().to(device) # NLLLoss
for epoch in range(0,epoches):
out = model(sample)
loss = cross_entropy_loss(out,y)
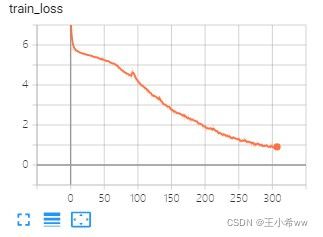
效果如下:
epoch = 302, train_loss = 0.8345055354858881, train_acc = 0.7542857142857143,test_loss = 24.628671884536743, test_acc = 0.002976190476190476
Epoch 304/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint303 is saved
Epoch 304/500: 100%|▉| 2800/2802 [01:22<00:00, 34.
epoch = 303, train_loss = 0.8892281786871276, train_acc = 0.7414285714285714,test_loss = 24.245324452718098, test_acc = 0.004464285714285714
Epoch 305/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint304 is saved
Epoch 305/500: 100%|▉| 2800/2802 [01:22<00:00, 34.
epoch = 304, train_loss = 0.8428794197631734, train_acc = 0.7507142857142857,test_loss = 22.60235471384866, test_acc = 0.005952380952380952
checkpoint305 is saved
Epoch 306/500: 100%|▉| 2800/2802 [01:22<00:00, 33.
epoch = 305, train_loss = 0.8745315343341125, train_acc = 0.7621428571428571,test_loss = 23.958800395329792, test_acc = 0.002976190476190476
Epoch 307/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint306 is saved
会发现,train_loss和test_loss相差太大,模型存在过拟合。
5、SphereFace loss(损失约束 - 2017 权重归一化)
参考
- SphereFace: A-Softmax Loss
- 【Paper】SphereFace: A-Softmax Loss
文章作者主要提出了归一化权值(normalize weights and zero biases) 和角度间距(angular margin),基于这2个点,对传统的softmax进行了改进,从而实现了最大类内距离小于最小类间距离的识别标准,得到Angular Margin softmax loss。
在softmax loss的基础增加 ∣ ∣ W ∣ ∣ = 1 , b = 0 ||W|| = 1, b=0 ∣∣W∣∣=1,b=0的约束,并引入夹角得出Modified Softmax Loss公式如下:
L m o d i f i e d = 1 N ∑ i − l o g ( e ∣ ∣ x i ∣ ∣ c o s ( θ y i , i ) ∑ j e ∣ ∣ x i ∣ ∣ c o s ( θ j , i ) ) L_{modified} = \frac{1}{N} \sum_i - log(\frac{e^{||x_i||cos(\theta_{y_i},i)}}{\sum_j e^{||x_i||cos(\theta_j,i)}}) Lmodified=N1i∑−log(∑je∣∣xi∣∣cos(θj,i)e∣∣xi∣∣cos(θyi,i))
其中 ∣ ∣ w i ∣ ∣ = 1 ||w_i|| = 1 ∣∣wi∣∣=1,因此指数部分如下所示,Modified Softmax Loss依然满足全连层的输出作为softmax函数的输入这项基本条件。
∣ ∣ x i ∣ ∣ c o s ( θ y i , i ) = w i × x i ∣ ∣ w i ∣ ∣ = w i × x i ||x_i||cos(\theta_{y_i},i) = \frac{w_i \times x_i}{||w_i||} = w_i \times x_i ∣∣xi∣∣cos(θyi,i)=∣∣wi∣∣wi×xi=wi×xi
原始softmax loss和Modified Softmax Loss的特征分布结果如下:发现经过M-softmax之后不同类别的特征区域大小基本一致。
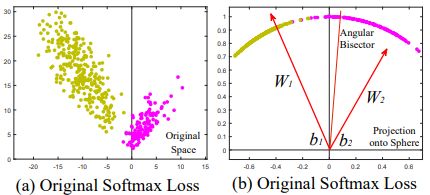
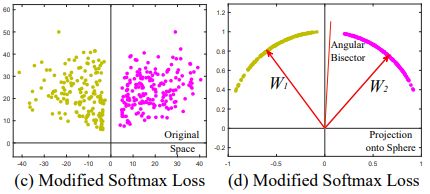
在此基础上,再引入angular,用m表示:
L a n g = 1 N ∑ i − l o g ( e ∣ ∣ x i ∣ ∣ c o s ( m θ y i , i ) e ∣ ∣ x i ∣ ∣ c o s ( m θ y i , i ) + ∑ j ≠ y i e ∣ ∣ x i ∣ ∣ c o s ( θ j , i ) ) L_{ang} = \frac{1}{N} \sum_i - log(\frac{e^{||x_i||cos(m\theta_{y_i},i)}}{e^{||x_i||cos(m\theta_{y_i},i)} +\sum_{j \neq y_i} e^{||x_i||cos(\theta_j,i)}}) Lang=N1i∑−log(e∣∣xi∣∣cos(mθyi,i)+∑j=yie∣∣xi∣∣cos(θj,i)e∣∣xi∣∣cos(mθyi,i))
经过化简之后最终产生Angular-softmax的loss公式:
L a n g = 1 N ∑ i − l o g ( e ∣ ∣ x i ∣ ∣ ψ ( θ y i , i ) e ∣ ∣ x i ∣ ∣ ψ ( θ y i , i ) + ∑ j ≠ y i e ∣ ∣ x i ∣ ∣ c o s ( θ j , i ) ) L_{ang} = \frac{1}{N} \sum_i - log(\frac{e^{||x_i||\psi(\theta_{y_i},i)}}{e^{||x_i||\psi(\theta_{y_i},i)} +\sum_{j \neq y_i} e^{||x_i||cos(\theta_j,i)}}) Lang=N1i∑−log(e∣∣xi∣∣ψ(θyi,i)+∑j=yie∣∣xi∣∣cos(θj,i)e∣∣xi∣∣ψ(θyi,i))
其中:
![]()
![]()
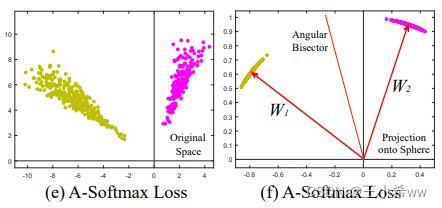
Angular Softmax Loss的特征分布结果如下:会发现A-Softmax不仅能对不同类别的特征生成大小基本一致的区域,而且类别间的间隔也很明显(类内聚合,类间分离)。
A-softmax与L-Softmax的区别:
A-Softmax与L-Softmax的最大区别在于A-Softmax的权重归一化了,而L-Softmax则没有。A-Softmax权重的归一化导致特征上的点映射到单位超球面上,而L-Softmax则不没有这个限制,这个特性使得两者在几何的解释上是不一样的。如果在训练时两个类别的特征输入在同一个区域时,如下图1所示。A-Softmax只能从角度上分度这两个类别,也就是说它仅从方向上区分类,分类的结果如图2所示;而L-Softmax,不仅可以从角度上区别两个类,还能从权重的模(长度)上区别这两个类,分类的结果如图3所示。在数据集合大小固定的条件下,L-Softmax能有两个方法分类,训练可能没有使得它在角度与长度方向都分离,导致它的精确可能不如A-Softmax。
1)源码
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
from torch.nn import Parameter
import math
def myphi(x,m):
x = x * m
return 1-x**2/math.factorial(2)+x**4/math.factorial(4)-x**6/math.factorial(6) + \
x**8/math.factorial(8) - x**9/math.factorial(9)
class AngleLinear(nn.Module):
def __init__(self, in_features, out_features, m = 4, phiflag=True):
super(AngleLinear, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.Tensor(in_features,out_features))
self.weight.data.uniform_(-1, 1).renorm_(2,1,1e-5).mul_(1e5)
self.phiflag = phiflag
self.m = m
self.mlambda = [
lambda x: x**0,
lambda x: x**1,
lambda x: 2*x**2-1,
lambda x: 4*x**3-3*x,
lambda x: 8*x**4-8*x**2+1,
lambda x: 16*x**5-20*x**3+5*x
]
def forward(self, input):
x = input # size=(B,F) F is feature len
w = self.weight # size=(F,Classnum) F=in_features Classnum=out_features
ww = w.renorm(2,1,1e-5).mul(1e5)
xlen = x.pow(2).sum(1).pow(0.5) # size=B
wlen = ww.pow(2).sum(0).pow(0.5) # size=Classnum
cos_theta = x.mm(ww) # size=(B,Classnum)
cos_theta = cos_theta / xlen.view(-1,1) / wlen.view(1,-1)
cos_theta = cos_theta.clamp(-1,1)
if self.phiflag:
cos_m_theta = self.mlambda[self.m](cos_theta)
theta = Variable(cos_theta.data.acos())
k = (self.m*theta/3.14159265).floor()
n_one = k*0.0 - 1
phi_theta = (n_one**k) * cos_m_theta - 2*k
else:
theta = cos_theta.acos()
phi_theta = myphi(theta,self.m)
phi_theta = phi_theta.clamp(-1*self.m,1)
cos_theta = cos_theta * xlen.view(-1,1)
phi_theta = phi_theta * xlen.view(-1,1)
output = (cos_theta,phi_theta)
return output # size=(B,Classnum,2)
class AngleLoss(nn.Module):
def __init__(self, gamma=0):
super(AngleLoss, self).__init__()
self.gamma = gamma
self.it = 0
self.LambdaMin = 5.0
self.LambdaMax = 1500.0
self.lamb = 1500.0
def forward(self, input, target):
self.it += 1
cos_theta,phi_theta = input
target = target.view(-1,1) #size=(B,1)
index = cos_theta.data * 0.0 #size=(B,Classnum)
index.scatter_(1,target.data.view(-1,1),1)
index = index.byte()
index = Variable(index)
self.lamb = max(self.LambdaMin,self.LambdaMax/(1+0.1*self.it ))
output = cos_theta * 1.0 #size=(B,Classnum)
output[index] -= cos_theta[index]*(1.0+0)/(1+self.lamb)
output[index] += phi_theta[index]*(1.0+0)/(1+self.lamb)
logpt = F.log_softmax(output)
logpt = logpt.gather(1,target)
logpt = logpt.view(-1)
pt = Variable(logpt.data.exp())
loss = -1 * (1-pt)**self.gamma * logpt
loss = loss.mean()
return loss
2)实验
使用angular_margin_softmax对MobileNetV3进行训练,简单修改如下:
class MobileNetV3_Large(nn.Module):
def __init__(self, num_classes=1000):
...
self.linear4 = nn.Linear(1280, 512)
self.angleLinear = AngleLinear(in_features=512,out_features=num_classes)
def forward(self, x):
out = self.hs1(self.bn1(self.conv1(x)))
out = self.bneck(out)
out = self.hs2(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, 7)
out = out.view(out.size(0), -1)
out = self.hs3(self.bn3(self.linear3(out)))
out = self.linear4(out)
out = self.angleLinear(out) #size = (B,Classnum,2),返回的是(cos_theta,phi_theta)
return out
...
#接着在train.py中使用NLLLoss即可
angle_loss = AngleLoss().to(device) #ArcFace输出结果是一个张量,不能进行反向传播,需要使用softmax函数(多类交叉熵)计算loss
for epoch in range(0,epoches):
...
out = model(sample) ## size=(B,Classnum,2)
loss = angle_loss(out,y) #A_softmax损失
...
train_loss += loss.item()
pred,pred_index = out[0].max(axis=1)
效果如下:
epoch = 5, train_loss = 6.160322679110935, train_acc = 0.004642857142857143,test_loss = 6.061383976822808, test_acc = 0.001488095238095238
checkpoint6 is saved
epoch = 6, train_loss = 6.13382915019989, train_acc = 0.007142857142857143,test_loss = 6.065926023891994, test_acc = 0.005952380952380952
checkpoint7 is saved
...
6、cosFace Loss(损失约束 - 2018 特征权重归一化)
参考
- cosface loss
- 【paper】CosFace: Large Margin Cosine Loss for Deep Face Recognition
CosFace(Additive Cosine margin)为加法余弦间隔,CosFace的 L M C L L_{MCL} LMCL(大间隔余弦损失函数)通过权重归一化,特征向量归一化到一个固定值s,并且让 c o s ( θ ) cos(θ) cos(θ)加上m(注意是加在了余弦上)进行softmax loss损失函数的优化。
L l m c = 1 / N ∑ i − l o g e s ( c o s ( θ y i , i ) − m ) e s ( c o s ( θ y i , i ) − m ) + ∑ j ≠ y i e s ( c o s ( θ j , i ) ) L_{lmc} = 1/N \sum_i - log\frac{e^{s(cos(\theta_{y_i},i) - m)}}{e^{s(cos(\theta_{yi,i})-m)} + \sum_{j \neq y_i}e^{s(cos(\theta_j,i))}} Llmc=1/Ni∑−loges(cos(θyi,i)−m)+∑j=yies(cos(θj,i))es(cos(θyi,i)−m)
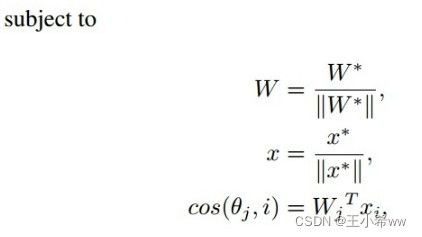
Note:这里的 c o s ( θ j , i ) cos(θ_j,i) cos(θj,i)是通过特征的线性加权计算得到的,因为余弦距离在Softmax loss中是这么计算的:
f j = W j T x = ∣ ∣ w j ∣ ∣ ⋅ ∣ ∣ x ∣ ∣ ⋅ c o s θ j f_j = W^T_jx = ||w_j|| \cdot ||x|| \cdot cos\theta_j fj=WjTx=∣∣wj∣∣⋅∣∣x∣∣⋅cosθj
不同损失函数的对比:
NSL是进行特征归一化的L2_softmax loss;A-Softmax是SphereFace loss;灰色部分是决策边界。
特征归一化处理的必要性:
原始未进行特征归一化的softmax loss既要学习特征向量的L2范数,又要学习特征向量和权重系数之间的夹角。强调L2范数去减小整体损失会弱化cosine的限制。距离来说,训练过程中调整容易区分的样本的特征范数比难以区分的样本的特征范数大得多的话,就可以很大程度上掩盖掉cosine函数的作用。如果加上特征的范数限制,那么cosine函数的值就直接决定分类的概率,那么训练完成后同一类样本的特征向量在超平面上就聚集到了一起,不同类的特征向量在超平面上就可以做到相互远离。
特征归一化的幅值s还必须足够大,这样所有的类别簇才可以在半径足够大的超球面上分散开。
s ≥ C − 1 C l o g ( C − 1 ) P W 1 − P W s \geq \frac{C-1}{C}log\frac{(C-1)P_W}{1 - P_W} s≥CC−1log1−PW(C−1)PW
C是要区分的类别数, P W P_W PW 是对每一类期望达到的最小分类准确率。
超参数m的设置规则
考虑二分类的情况,NSL的决策边界是 cos ( θ 1 ) − cos ( θ 2 ) = 0 \cos(\theta_1)-\cos(\theta_2)=0 cos(θ1)−cos(θ2)=0 ,如下图所示。从图上可以看出,对决策边界附近的样本, cos ( θ 1 ) \cos(\theta_1) cos(θ1)和 cos ( θ 2 ) \cos(\theta_2) cos(θ2) 很接近,它的类别是模糊不清的,就是把它分到哪一类都可以。而对于LMCL,对于类别1,其决策边界是 cos ( θ 1 ) − cos ( θ 2 ) = m \cos(\theta_1) - \cos(\theta_2) = m cos(θ1)−cos(θ2)=m也就是要求 θ 1 \theta_1 θ1要比 θ 2 \theta_2 θ2小很多。因此,类内的变化空间被压缩了,类间的变化空间被加大了。
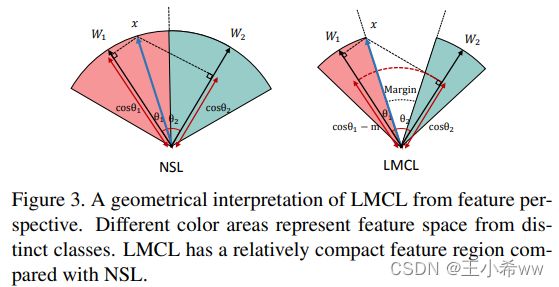
理论上,最优的分类结果是每一类的特征向量都与该类的权重W之间的夹角很小,也就是特征向量都分布在其所隶属的类权重向量的周围。那么理论上,m的取值范围为 0 ≤ m ≤ ( 1 − m a x ( W i T W j ) ) 0 \leq m \leq (1 - max(W_i^TW_j)) 0≤m≤(1−max(WiTWj)),m要大于等于0很好理解,之所以m要小于 ( 1 − m a x ( W i T W j ) ) (1 - max(W_i^TW_j)) (1−max(WiTWj))是因为,对于不同类别的样本,其最好情况下是分布在各自类别权重向量 W i W_i Wi 的周围,那么 W i T W j = ∣ ∣ W i ∣ ∣ ∣ ∣ W j ∣ ∣ cos ( θ i j ) = cos ( θ i j ) W_i^TW_j=||W_i||||W_j||\cos(\theta_{ij})=\cos(\theta_{ij}) WiTWj=∣∣Wi∣∣∣∣Wj∣∣cos(θij)=cos(θij), θ i j θ_{ij} θij就是上图右图中红色虚线表示的夹角,m肯定应该小于 cos ( θ i j ) \cos(\theta_{ij}) cos(θij)。m的取值范围应该为:
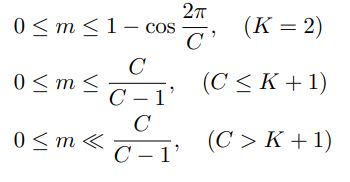
C是分类类别数,K是学习的特征的维度。作者举了个例子,8类人脸在不同m情况下学到的特征的分布情况。
由于C等于8,K=2方便可视化,所以 m ≤ 1 − cos ( 2 π ) 8 ≈ 0.29 m \leq 1 - \frac{\cos(2\pi)}{8} \approx 0.29 m≤1−8cos(2π)≈0.29
所以作者设置m为0,0.1,0.2.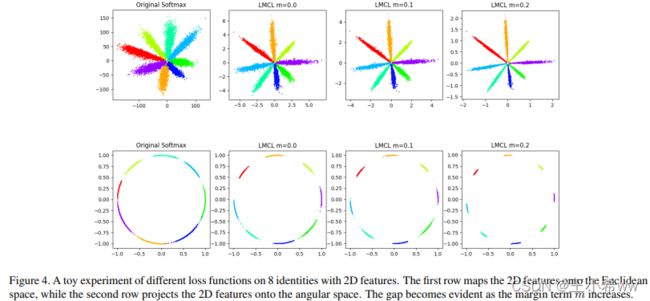
从上图可以看出,m越大,学习到的特征的判别力越好。
1)源码
import torch
import torch.nn as nn
import torch.nn.functional as F
#参考 https://blog.csdn.net/qq_34914551/article/details/104522030
class CosFaceLoss(nn.Module):
r"""Implement of large margin cosine distance: :
Args:
in_features: size of each input sample
out_features: size of each output sample
s: norm of input feature
m: margin
cos(theta) - m
"""
def __init__(self, in_features, out_features, s=30.0, m=0.40):
super(CosFaceLoss, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.s = s
self.m = m
self.weight = nn.Parameter(torch.FloatTensor(out_features, in_features))
nn.init.xavier_uniform_(self.weight)
def forward(self, input, label):
# --------------------------- cos(theta) & phi(theta) ---------------------------
cosine = F.linear(F.normalize(input), F.normalize(self.weight))
phi = cosine - self.m
# --------------------------- convert label to one-hot ---------------------------
one_hot = torch.zeros(cosine.size(), device='cuda')
# one_hot = one_hot.cuda() if cosine.is_cuda else one_hot
one_hot.scatter_(1, label.view(-1, 1).long(), 1)
# -------------torch.where(out_i = {x_i if condition_i else y_i) -------------
output = (one_hot * phi) + ((1.0 - one_hot) * cosine)
# you can use torch.where if your torch.__version__ is 0.4
output *= self.s
# print(output)
return output
def __repr__(self):
return self.__class__.__name__ + '(' \
+ 'in_features=' + str(self.in_features) \
+ ', out_features=' + str(self.out_features) \
+ ', s=' + str(self.s) \
+ ', m=' + str(self.m) + ')'
2)实验
使用cosFace loss对MobileNetV3进行训练,简单修改如下:
class MobileNetV3_Large(nn.Module):
def __init__(self, num_classes=1000):
...
self.linear4 = nn.Linear(1280, 512) #输出维数从num_classes修改为512
self.cosFace_loss = CosFaceLoss(in_features=512,out_features=num_classes)
def forward(self, x, y):
out = self.hs1(self.bn1(self.conv1(x)))
out = self.bneck(out)
out = self.hs2(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, 7)
out = out.view(out.size(0), -1)
out = self.hs3(self.bn3(self.linear3(out)))
out = self.linear4(out)
out = self.cosFace_loss(out,y)
return out
...
#接着在train.py中使用NLLLoss即可
softmax_loss = nn.CrossEntropyLoss().to(device) # NLLLoss
for epoch in range(0,epoches):
...
out = model(sample,y)
loss = cross_entropy_loss(out,y)
效果如下:
epoch = 0, train_loss = 19.490150450297765, train_acc = 0.0,test_loss = 18.7509761991955, test_acc = 0.0
checkpoint1 is saved
Epoch 2/500: 100%|▉| 2800/2802 [01:26<00:00, 32.31
epoch = 1, train_loss = 18.732188301086424, train_acc = 0.0,test_loss = 18.819916827338083, test_acc = 0.0
checkpoint2 is saved
Epoch 3/500: 100%|▉| 2800/2802 [01:25<00:00, 32.62
epoch = 2, train_loss = 18.447026476178852, train_acc = 0.0,test_loss = 18.377974646432058, test_acc = 0.0
checkpoint3 is saved
Epoch 4/500: 100%|▉| 2800/2802 [01:25<00:00, 32.57
epoch = 3, train_loss = 18.306991988590784, train_acc = 0.0,test_loss = 18.21899235816229, test_acc = 0.0
checkpoint4 is saved
Epoch 5/500: 100%|▉| 2800/2802 [01:25<00:00, 32.61
epoch = 4, train_loss = 18.136429609571184, train_acc = 0.0,test_loss = 18.920511461439588, test_acc = 0.0
Epoch 6/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint5 is saved
7、ArcFace loss(损失约束 - 2018 特征权重归一化)
参考
- ArcFace解析
ArcFace loss:Additive Angular Margin Loss(加性角度间隔损失函数),对特征向量和权重归一化,对θ加上角度间隔m,角度间隔比余弦间隔在对角度的影响更加直接。几何上有恒定的线性角度margen。
- ArcFace中是直接在角度空间θ中最大化分类界限,而CosFace是在余弦空间cos(θ)中最大化分类界限。
- 预处理(人脸对齐):人脸关键点由MTCNN检测,再通过相似变换得到了被裁剪的对齐人脸。
- 训练(人脸分类器):ResNet50 + ArcFace loss
- 测试:从人脸分类器FC1层的输出中提取512维的嵌入特征,对输入的两个特征计算余弦距离,再来进行人脸验证和人脸识别。
- 实际代码中训练时分为resnet model+arc head+softmax loss。resnet model输出特征;arc head将特征与权重间加上角度间隔后,再输出预测标签,求ACC时就用这个输出标签;softmax loss求预测标签和实际的误差。
- LFW上99.83%,YTF上98.02%
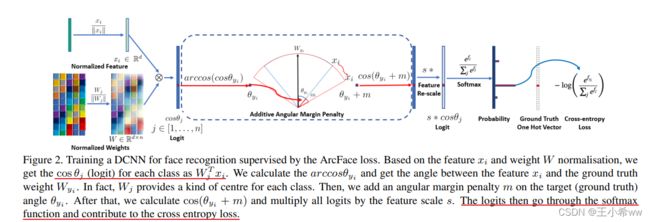
ArcFace loss实现过程:
ArcFace loss损失函数如下:
L = − 1 N ∑ i = 1 N l o g e s ( c o s ( θ y i + m ) ) e s ( c o s ( θ y i + m ) ) + ∑ j = 1 , j ≠ y i n e s ⋅ c o s θ j L = - \frac{1}{N} \sum_{i=1}^N log \frac{e^{s(cos(\theta_{y_i}+m))}}{e^{s(cos(\theta_{y_i}+m))} + \sum_{j=1,j \neq y_i}^n e^{s\cdot cos\theta_j}} L=−N1i=1∑Nloges(cos(θyi+m))+∑j=1,j=yines⋅cosθjes(cos(θyi+m))
在 x i x_i xi和 W j i W_{ji} Wji之间的θ上加上角度间隔m(注意是加在了角θ上),以加法的方式惩罚深度特征与其相应权重之间的角度,从而同时增强了类内紧度和类间差异。
惩罚θ角度的意思就是:训练时加上m就会使θ降低
解释Margin是如何使类内聚合类间分离的:比如训练时降到某一固定损失值时,有Margin和无Margin的e指数项是相等的,则有Margin的 θ y i θ_{yi} θyi就需要相对的减少了。这样来看有 Margin的训练就会把 i 类别的输入特征和权重间的夹角 θ y i θ_{yi} θyi缩小了,从一些角度的示图中可以看出,Margin把 θ y i θ_{yi} θyi挤得更类内聚合了, θ y i θ_{yi} θyi和其他θ类间也就更分离了。
L2归一化来修正单个权重 ∣ ∣ W j ∣ ∣ = 1 ||W_j||=1 ∣∣Wj∣∣=1(和L2_softmax有点像,都需要进行特征归一化约束之后,再使用softmax loss),还通过L2归一化来固定嵌入特征 ∣ ∣ x i ∣ ∣ ||x_i|| ∣∣xi∣∣,并将其重新缩放成s。特征和权重的归一化步骤使预测仅取决于特征和权重之间的角度。因此,所学的嵌入特征分布在半径为s的超球体上。
由于提出的加性角度间隔(additive angular margin)惩罚与测地线距离间隔(geodesic distance margin)惩罚在归一化的超球面上相等,因此我们将该方法命名为ArcFace。
Arcface的优点
性能高,易于编程实现,复杂性低,训练效率高
ArcFace直接优化geodesic distance margin(弧度),因为归一化超球体中的角和弧度的对应。ArcFace比Softmax的特征分布更紧凑,决策边界更明显,一个弧长代表一个类。
为了性能的稳定,ArcFace不需要与其他loss函数实现联合监督,可以很容易地收敛于任何训练数据集。
1)源码解析
#参考 https://blog.csdn.net/qq_40859461/article/details/86771136
import math
import torch
from torch import nn
from torch.nn import Parameter
import torch.nn.functional as F
class ArcFaceLoss(nn.Module):
def __init__(self, in_feature=128, out_feature=10575, s=32.0, m=0.50, easy_margin=False):
super(ArcFaceLoss, self).__init__()
self.in_feature = in_feature
self.out_feature = out_feature
self.s = s
self.m = m
self.weight = Parameter(torch.Tensor(out_feature, in_feature))
nn.init.xavier_uniform_(self.weight) #初始化卷积核: 目的是为了使得每一层的方差都尽可能相等, 使网络中的信息更好地流动. 则将每一层权重初始化为如下范围内的均匀分布
self.easy_margin = easy_margin
self.cos_m = math.cos(m)
self.sin_m = math.sin(m)
# make the function cos(theta+m) monotonic decreasing while theta in [0°,180°]
self.th = math.cos(math.pi - m)
self.mm = math.sin(math.pi - m) * m
def forward(self, x, label):
# cos(theta)
cosine = F.linear(F.normalize(x), F.normalize(self.weight)) #包含特征和权重的归一化操作
# cos(theta + m)
sine = torch.sqrt(1.0 - torch.pow(cosine, 2))
phi = cosine * self.cos_m - sine * self.sin_m
if self.easy_margin:
phi = torch.where(cosine > 0, phi, cosine)
else:
phi = torch.where((cosine - self.th) > 0, phi, cosine - self.mm)
#one_hot = torch.zeros(cosine.size(), device='cuda' if torch.cuda.is_available() else 'cpu')
one_hot = torch.zeros_like(cosine)
one_hot.scatter_(1, label.view(-1, 1), 1)
output = (one_hot * phi) + ((1.0 - one_hot) * cosine)
output = output * self.s
return output
2)实验
class MobileNetV3_Large(nn.Module):
def __init__(self, num_classes=1000):
...
self.linear4 = nn.Linear(1280, 512) #输出维数从num_classes修改为512
self.arc_loss = ArcFaceLoss(in_feature=512, out_feature=num_classes,
m=0.5) # ArcFace损失函数,输入的特征维数为身份类别数,输出特征维数为512,间隔m为0.3(自动进行特征和参数的归一化处理)
def forward(self, x, y):
out = self.hs1(self.bn1(self.conv1(x)))
out = self.bneck(out)
out = self.hs2(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, 7)
out = out.view(out.size(0), -1)
out = self.hs3(self.bn3(self.linear3(out)))
out = self.linear4(out)
out = self.arc_loss(out,y) #Arcface损失
return out
...
#接着在train.py中使用NLLLoss即可
softmax_loss = nn.CrossEntropyLoss().to(device) # NLLLoss
for epoch in range(0,epoches):
out = model(sample, y)
loss = cross_entropy_loss(out,y)
实验效果
Epoch 1/100: 100%|▉| 47568/47571 [46:39<00:00, 16.
epoch = 0, train_loss = 15.873860453981925, train_acc = 0.0,test_loss = 14.844074659837949, test_acc = 0.0
Epoch 2/100: 0%| | 0/47571 [00:00<?, ?img/s]checkpoint1 is saved
Epoch 2/100: 100%|▉| 47568/47571 [25:02<00:00, 31.
epoch = 1, train_loss = 13.400763185586426, train_acc = 0.0,test_loss = 14.149169119580776, test_acc = 0.0
checkpoint2 is saved
Epoch 3/100: 100%|▉| 47568/47571 [22:34<00:00, 35.WARNING:root:NaN or Inf found in input tensor.
Epoch 3/100: 100%|▉| 47568/47571 [25:00<00:00, 31.
epoch = 2, train_loss = nan, train_acc = 0.0009670366633030609,test_loss = nan, test_acc = 0.0015405864853378665
checkpoint3 is saved
Epoch 4/100: 100%|▉| 47568/47571 [22:39<00:00, 35.WARNING:root:NaN or Inf found in input tensor.
Epoch 4/100: 100%|▉| 47568/47571 [25:05<00:00, 31.
epoch = 3, train_loss = nan, train_acc = 0.0015556676757484023,test_loss = nan, test_acc = 0.0015405864853378665
会发现,当lr=0.01,epoch=2时,arcFace计算的损失值为nan,浏览了各大网站,解决方法有如下几种
- 降低学习率lr
- 增大模型训练时的batch_size,batch size最好是128,用多个GPU训练。参考https://github.com/deepinsight/insightface/issues/74
- 使用centerLoss或者L2-softmax进行模型预训练,参考https://github.com/deepinsight/insightface/issues/387
- 检查一下该损失函数在模型中是否用得正确,输出结果的取值范围是否在损失函数的定义域内。
3)ArcFace Loss为Nan怎么解决
参考
- 警惕!损失Loss为Nan或者超级大的原因
- Pytorch训练网络模型过程中Loss为负值的问题及其解决方案
- https://github.com/deepinsight/insightface/issues/1664
解决方法:
使用L2-softmax(看上面L2_softmax实验,模型过拟合了)的预训练权重文件进行模型加载,以及将lr调整值0.005,train_loss和test_loss终于可以同时下降了(我感觉是学习率起的作用)。
Epoch 1/500: 100%|▉| 2800/2802 [01:28<00:00, 31.53
epoch = 0, train_loss = 10.648999228818075, train_acc = 0.016428571428571428,test_loss = 9.672125000329245, test_acc = 0.025297619047619048
checkpoint1 is saved
Epoch 2/500: 100%|▉| 2800/2802 [01:27<00:00, 32.07
epoch = 1, train_loss = 10.117614848954338, train_acc = 0.01892857142857143,test_loss = 9.23866881359191, test_acc = 0.022321428571428572
checkpoint2 is saved
Epoch 3/500: 100%|▉| 2800/2802 [01:26<00:00, 32.20
epoch = 2, train_loss = 9.56589084471975, train_acc = 0.02142857142857143,test_loss = 8.703474456355686, test_acc = 0.03571428571428571
checkpoint3 is saved
...
epoch = 34, train_loss = 6.7769753401620045, train_acc = 0.09892857142857144,test_loss = 7.465910258747282, test_acc = 0.11160714285714286
checkpoint35 is saved
Epoch 36/500: 100%|▉| 2800/2802 [01:25<00:00, 32.6
epoch = 35, train_loss = 6.83953810266086, train_acc = 0.10107142857142858,test_loss = 7.755035051277706, test_acc = 0.09523809523809523
checkpoint36 is saved
Epoch 37/500: 100%|▉| 2800/2802 [01:25<00:00, 32.6
epoch = 36, train_loss = 7.095788996134486, train_acc = 0.09142857142857143,test_loss = 8.262529448384331, test_acc = 0.08928571428571429
Epoch 38/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint37 is saved
但是用MobileNetV3 + arcFace loss训练的模型会发现模型容易过拟合,train_loss和test_loss虽然都会下降,但是值相差有点大
Epoch 126/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint125 is saved
Epoch 126/500: 100%|▉| 2800/2802 [01:25<00:00, 32.
epoch = 125, train_loss = 4.749639714328306, train_acc = 0.20285714285714285,test_loss = 7.780712046438739, test_acc = 0.15625
checkpoint126 is saved
Epoch 127/500: 100%|▉| 2800/2802 [01:25<00:00, 32.
epoch = 126, train_loss = 4.593655687602503, train_acc = 0.21392857142857144,test_loss = 7.834138387725467, test_acc = 0.11011904761904762
Epoch 128/500: 0%| | 0/2802 [00:00<?, ?img/s]checkpoint127 is saved
Epoch 128/500: 100%|▉| 2800/2802 [01:25<00:00, 32.
epoch = 127, train_loss = 4.784141867070326, train_acc = 0.18321428571428572,test_loss = 7.470722722155707, test_acc = 0.14732142857142858
可以考虑使用HRNetV2进行训练。
8、参考源码
- 【本文实验源码】
- InsightFace人脸识别系统(Danbin)
- insightFace工程源码(含ArcFace,RetinaFace等人脸检测模型)
- yingguobing/ArcFace - TensorFlow 2.4实现
- ArcFace Loss源码(pytorch)
- centerLoss源码(pytorch)
- sphereface loss源码(pytorch)