遗落在时光里的静态链表（线性表的静态存储）---C语言版

众所周知，指针是c语言的灵魂，指针使得链表的实现简单明了起来。
但是问题来了，在c语言还没有的时代，又想描述链表，怎么办呢？
这就有了我们今天的主角静态链表

首先，我们来解决一个最重要的问题，没有指针，怎么表示下一个元素的位置呢？

当时的人们想出来的办法便是，用数组的下标来代替指针。我们把这个数组的下标叫做游标。

第二个问题，当我们要往数组里插入元素时，如何确定数组里哪些分量未被使用，要插到哪个位置上呢？当我们删除一个元素的时候，要把这个删除后已经不存放数据的数组分量链接到哪里去，然后再次被使用呢？

解决办法是将所有未被使用过的以及被删除的分量用一个游标链成一个备用链表。
每当进行插入的使用便从备用链表上取得第一个结点作为待插入的新结点。
反之，在删除时将从链表中删除下来结点链接到备用链表上。

有没有觉得上面的描述特别熟悉，这实际上就是C语言里面malloc函数和free函数做得事情，在静态链表中，我们得自己实现，不过操作起来也不复杂。

最后一个问题，我们现在已经知道了我们把静态链表分为两部分，一部分存放数据，一部分不存放数据，我们称之为备用链表。那么我们如何标识这两部分呢？

解决办法，我们这里把数组下标为0位置的游标用来存放备用链表的第一个元素（也就是数组中第一个不存放数据的元素）的下标
我们这里把数组下标为1的位置游标用来存放第一个数据不为空的元素的下标
这里还有个细节就是我们把游标为0设为这两部分的结束。

看到这里，关于静态链表的相关问题都解决得差不多了，我们开始动手设计它吧。假定我们有一个长度为10的数组。如下所示：

下标0:数据不存放任何东西，游标用来指向数组当中第一个不存放数据的元素。（这里指向6）
下标1:数据不存放任何东西，游标用来指向数组当中第一个存放数据的元素。（这里指向2）
下标2到5：这部分存放了数据，最后一个存放数据的元素的游标为0.（这里下标为5的游标为0，表示最后一个存放数据的元素）
下标6-9：这部分不存放数据，备用链表，最后一个可被使用的元素的游标为0（这里下标为9的游标为0）

接下来我们就可以正式实现它了。

静态链表的定义

步骤一：定义数据元素类型

#define ElemType char//这里我们使用的例子，采取字符

步骤二：定义静态链表

#define MaxSize 10  //链表的最大长度
typedef struct{
    ElemType data;//存储的数据元素
    int next;//游标，用来指示下一个数组分量的下标
}SLinkList[MaxSize];//静态链表

静态链表的操作

初始化

/*初始化*/
int InitSpace_SL(SLinkList space){ 
  int i;
  for (i = 2; i < MaxSize-1; i++){
      space[i].data=' ';
      space[i].next=i+1;
  }
  space[0].next=2;
  space[0].data=' ';
  space[1].next=0;
  space[1].data=' ';
  space[MaxSize-1].next=0;
  space[MaxSize-1].data=' ';
  return TRUE;
}

运行打印结果：

初始化成功
数组下标=0,数据= ,游标为2
数组下标=1,数据= ,游标为0
数组下标=2,数据= ,游标为3
数组下标=3,数据= ,游标为4
数组下标=4,数据= ,游标为5
数组下标=5,数据= ,游标为6
数组下标=6,数据= ,游标为7
数组下标=7,数据= ,游标为8
数组下标=8,数据= ,游标为9
数组下标=9,数据= ,游标为0

初始化后的空表如下所示：

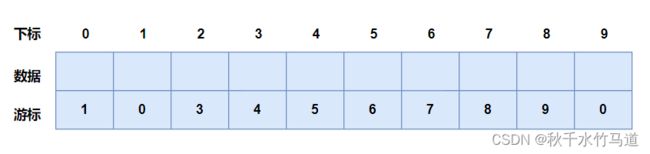
那么不顺便好奇一下表满了长什么样吗？

求表长

/*求表长*/
int ListLength(SLinkList space){
    int length=0;//空表长度为0
    int i=space[1].next;//指向第一个有数据的位置
    while (i!=0){
        length++;
        i=space[i].next;//相当于指针的p=p->next
    }
    return length;
}

主要的操作便是遍历表：
这里的i=space[i].next;相当于指针的p=p->next

分配空间

int Malloc_SL(SLinkList space){
    int i=space[0].next;//指向第一个没有数据的位置
    if(space[0].next) space[0].next=space[i].next;//如果还有空间，让space[0].next指向下一个空闲位置
    return i;//返回这个空闲位置
}

具体讲解和插入操作一块，这里就不重复啦

回收空间

void Free_SL(SLinkList space,int k){
    space[k].data=' ';
    space[k].next=space[0].next;
    space[0].next=k;
}

具体讲解和删除操作一块，这里就也不重复啦

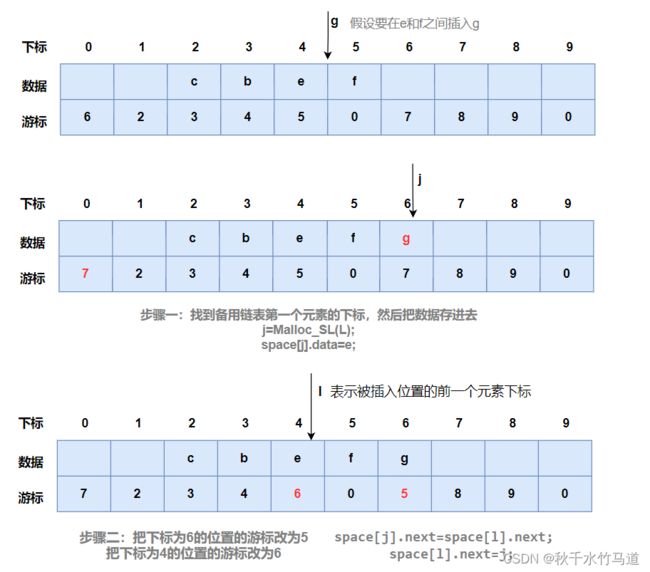
插入操作

/*插入*/
int ListInsert_SL(SLinkList space,int i,ElemType e){
   int j,k,l;
   if(i<1||i>ListLength(space)+1) return FALSE;//位序无效
   j=Malloc_SL(space);//找到备用链表的第一个元素位置
   if (j!=0){//分配成功
       space[j].data=e;
       l=1;
       for ( k = 1; k < i; k++){//找到插入元素位序的前一个位置
           l=space[l].next;
       }
       space[j].next=space[l].next;
       space[l].next=j;
   } 
} 

废话不多说，有图有真相

删除操作

/*删除*/
int ListDelete_SL(SLinkList space,int i){   
    int k,l;
   if(i<1||i>ListLength(space)) return FALSE;//位序无效
       l=1;
       for ( k = 1; k < i; k++){//找到删除位序的前一个位置
           l=space[l].next;
       }
       k=space[l].next;
       space[l].next=space[k].next;
       Free_SL(space,k);//回收结点
}

还是废话不多说，有图有真相

其他操作

剩下的按值查找，按位查找，还有打印，无非就是遍历链表，为了不使文章
冗余，最后附上完整操作。这里就不写了。

完整源代码

#include
#include
#define TRUE 1
#define FALSE 0

#define ElemType char//这里我们使用的例子采取字符

#define MaxSize 10  //静态链表的最大长度
typedef struct{
    ElemType data;//存储的数据元素
    int next;//游标，用来指示下一个数组分量的下标
}SLinkList[MaxSize];//静态链表

/*初始化*/
int InitSpace_SL(SLinkList space){ 
  int i;
  for (i = 2; i < MaxSize-1; i++){
      space[i].data=' ';
      space[i].next=i+1;
  }
  space[0].next=2;
  space[0].data=' ';
  space[1].next=0;
  space[1].data=' ';
  space[MaxSize-1].next=0;
  space[MaxSize-1].data=' ';
  return TRUE;
}

int Malloc_SL(SLinkList space){
    int i=space[0].next;
    if(space[0].next) space[0].next=space[i].next;
    return i;
}

void Free_SL(SLinkList space,int k){
    space[k].data=' ';
    space[k].next=space[0].next;
    space[0].next=k;
}
/*求表长*/
int ListLength(SLinkList space){
    int length=0;
    int i=space[1].next;
    while (i!=0){
        length++;
        i=space[i].next;
    }
    return length;
}

/*插入*/
int ListInsert_SL(SLinkList space,int i,ElemType e){
   int j,k,l;
   if(i<1||i>ListLength(space)+1) return FALSE;
   j=Malloc_SL(space);
   if (j!=0){
       space[j].data=e;
       l=1;
       for ( k = 1; k < i; k++){
           l=space[l].next;
       }
       space[j].next=space[l].next;
       space[l].next=j;
   } 
} 

/*删除*/
int ListDelete_SL(SLinkList space,int i){   
    int k,l;
   if(i<1||i>ListLength(space)) return FALSE;
       l=1;
       for ( k = 1; k < i; k++){
           l=space[l].next;
       }
       k=space[l].next;
       space[l].next=space[k].next;
       Free_SL(space,k);
}

/*按值查找*/
int LocateElem_SL(SLinkList space,ElemType e){
    int i=space[1].next;
    while (i!=0){
        if (space[i].data==e) return TRUE;
        i=space[i].next;
    }
    return FALSE;
}

/*按位查找*/
ElemType GetElem_SL(SLinkList space,int i){
    int l,k;
    if(i<1||i>ListLength(space)) return ' '; //不在有效范围内
    l=1;
    for ( k = 1; k <= i; k++){
           l=space[l].next;
    }
    return space[l].data;
}

/*打印*/
void PrintSpace_SL(SLinkList space){
    int i;
    for (i = 0; i < MaxSize; i++){
        printf("数组下标=%d,数据=%c,游标为%d\n",i,space[i].data,space[i].next);
    }   
}


int main(void){
///初始化
    
    SLinkList L;
    int i=InitSpace_SL(L);
    if (i==1){
        printf("初始化成功\n");
    }else{
        printf("初始化失败\n"); 
    }
    PrintSpace_SL(L);
    i=ListLength(L);
    printf("长度为%d\n",i);
    printf("\n");    
/插入
    ElemType a[4]={'c','b','e','f'};
    int j;
    for ( j = 0; j < 4; j++){
        i=ListInsert_SL(L,j+1,a[j]);
    }
    PrintSpace_SL(L);

    i=ListLength(L);
    printf("长度为%d\n",i);
    printf("\n"); 

    i=ListInsert_SL(L,4,'g');
    if (i==0){
        printf("插入位序无效！"); 
    }else{
        printf("插入成功！\n"); 
        PrintSpace_SL(L);
    }
    printf("\n"); 

删除
    
    i=ListDelete_SL(L,2);    
    if (i==0){
        printf("删除位序无效！"); 
    }else{
        printf("删除成功！\n"); 
        PrintSpace_SL(L);
    }
    printf("\n"); 
//按值查找
    i=LocateElem_SL(L,'a');    
    if (i==1){
        printf("按值查找成功\n");
    }else{
        printf("按值查找失败\n"); 
    }
    printf("\n");     
//按位查找
    ElemType e;
    e=GetElem_SL(L,2);    
    if (e==' '){
        printf("按值查找失败\n"); 
    }else{
        printf("查找到的元素为：%c",e);
    }

//    

}

运行结果

初始化成功
数组下标=0,数据= ,游标为2
数组下标=1,数据= ,游标为0
数组下标=2,数据= ,游标为3
数组下标=3,数据= ,游标为4
数组下标=4,数据= ,游标为5
数组下标=5,数据= ,游标为6
数组下标=6,数据= ,游标为7
数组下标=7,数据= ,游标为8
数组下标=8,数据= ,游标为9
数组下标=9,数据= ,游标为0
长度为0

数组下标=0,数据= ,游标为6
数组下标=1,数据= ,游标为2
数组下标=2,数据=c,游标为3
数组下标=3,数据=b,游标为4
数组下标=4,数据=e,游标为5
数组下标=5,数据=f,游标为0
数组下标=6,数据= ,游标为7
数组下标=7,数据= ,游标为8
数组下标=8,数据= ,游标为9
数组下标=9,数据= ,游标为0
长度为4

插入成功！
数组下标=0,数据= ,游标为7
数组下标=1,数据= ,游标为2
数组下标=2,数据=c,游标为3
数组下标=3,数据=b,游标为4
数组下标=4,数据=e,游标为6
数组下标=5,数据=f,游标为0
数组下标=6,数据=g,游标为5
数组下标=7,数据= ,游标为8
数组下标=8,数据= ,游标为9
数组下标=9,数据= ,游标为0

删除成功！
数组下标=0,数据= ,游标为3
数组下标=1,数据= ,游标为2
数组下标=2,数据=c,游标为4
数组下标=3,数据= ,游标为7
数组下标=4,数据=e,游标为6
数组下标=5,数据=f,游标为0
数组下标=6,数据=g,游标为5
数组下标=7,数据= ,游标为8
数组下标=8,数据= ,游标为9
数组下标=9,数据= ,游标为0

按值查找失败

查找到的元素为：e

总结一下

尽管我们现在有了单链表，也不再会使用静态链表了，但是它的思想还是挺神奇的。
总的来说，它和单链表很像，插入删除不需要移动元素，所有我们称之为静态链表。
但是它不仅有单链表不能随机存取的缺点，也没有解决连续分配（数组）带来的表长难以确定的问题。