第十二届蓝桥杯大赛软件赛省赛B组题解

A：空间

题目描述：

分析：
1MB = 2^20B
32位=32/8 B = 4B.
2 ^10 = 1024
嗷嗷，这大概就是告诉我们基础知识的重要性吧，上课一定要注意听讲@^@

#include 
using namespace std;
int main(void){
	cout << 256 / 4 * 1024 * 1024<<endl;
	return 0;
}

答案：67108864

B：卡片

分析：
本题考察的也较为基础，当时脑子里闪过一个念头：第一个用完的数字是1？！， 还好还好，立马否定该想法，最后用完的谁也不知道是谁呢，所以0-9，都需要计数等操作吧。。
当时立马就想到了数组计数，下标代表的就是代指的数字了，arr[1] = k, 就表示数字1还剩下k个。

一大错因，不知使多少英雄好汉哂然泪下…
我们最后的答案应该是i - 1, 即i这个数是已经不能拼成的了。。

#include 
using namespace std;
int arr[10];
int main(void){
	for(int i = 0; i <= 9; i ++){
		arr[i] = 2021;
	}
	int i;
	int flag = 0;
	for(i = 1; ; i ++){
		int t = i;
		while(t){
			int r = t % 10;
			arr[r] --;
			t /= 10;
			if(arr[r] < 0){
				flag = 1;
			    break;
			}
		}
		if(flag) break;
	}
	cout << i - 1;
	return 0;
}

答案：3181

C：直线

分析

1. 当时想到一条直线可以表示成y = kx + b无非就是斜率k和截距b两个参数便可确定，使用map去重，便可得答案。but ,but，这些斜线的斜率不一定就是整数啊，即便我们用double存储，也会有精度误差，如何判断两斜线是否为同一条？即我们判断的标准何在？？判断两个数的差<10^-8次方便可认为两数相等
2. y = kx+b, 漏掉了斜率不存在的直线。最后需要加上。
3. 补充一点，我们需要拍一下序的，跟他的上一个数比较是否重复即可。

#include 
#include 
using namespace std;
const int N = 200000;
struct Line{
	double k, b;
}l[N];
bool cmp(Line a, Line b){
	if(a.k != b.k) {
		return a.k < b.k;
	}
	return a.b < b.b;
}
int main(void){
	int n;
	for(int x1 = 0; x1 < 20; x1 ++){
		for(int y1 = 0; y1 < 21; y1 ++){
			for(int x2 = 0; x2 < 20; x2 ++){
				for(int y2 = 0; y2 < 21; y2 ++){
					if(x1 != x2){
						double k = (double)(y1-y2)/(x1-x2);
						double b = y1 - k * x1;
						l[n ++] = {k, b};
					}
				}
			}
		}
	}
	sort(l, l + n, cmp);
	int res = 1;
	for(int i = 1; i < n; i ++){
		if(fabs(l[i].k - l[i-1].k) > 1e-8 || fabs(l[i].b - l[i-1].b) > 1e-8){
			res ++;
		}
	}
	cout << res + 20 << endl;
	return 0;
}

答案：40257

D:货物摆放

分析

1. 像这种题，当时直接想的暴力三重循环，开的unsigned long long。。。当时的我 艰辛 坚信只要我在循环里加足了条件，努力不让他溢出，加足了break，就会运行出来。。嗷嗷，显然，这个想法是不成熟的。。

2. 害，其实， 只要我们稍加优化，即把这么长的数的因子全部存起来，最后一个三重循环（长宽高）符合条件直接++即可。

3. 其实我们不难想到用一个数组来存，但是达不到去重的效果。是不是这个理？连续的两个三，我们第一层循环若是代表的长，我们会使用两遍3，那么长是3对应的可行方案数，也会重复，， 嗷嗷，细细品味，也到别有一番滋味

4. int(按照四字节计算)存储的最大正整数：21 4748 3647即21亿多点。long long （按照8字节计算）存储的最大正整数：922 3372 0368 5477 5807, 一共19位。

#include 
#include 
using namespace std;
typedef pair<long long, int>PII;
set<PII>st;
int main(void){
	long long n, i;
	int cnt = 0;
	n = 2021041820210418;
	for(i = 1; i * i <= n; i ++){
		if(n % i == 0){
			st.insert({i, 1});
			st.insert({n/i, 1});
		}
	}
	long long  ans = 0;
	for(auto it : st){
		for(auto it2 : st){
			for(auto it3 : st){
				if((it.first) * (it2.first)* (it3.first) == n){
					ans ++;
				}
			}
		}
	}
	cout << ans;
	return 0;
}

我人可能傻了。其实不需要这么set折腾的，我们在判断是不是有重复的直接加入数组时加一个判断即可if(n / i != i)
代码如下：

#include 
#include 
using namespace std;
vector<long long> vec;
int main(void){
	long long n = 2021041820210418;
	for(long long i = 1; i * i <= n; i ++){
		if(n % i == 0){
			vec.push_back(i);
			if(n / i != i) vec.push_back(n/i);
		}
	}
	int res = 0;
	for(auto a:vec){
		for(auto b:vec){
			for(auto c:vec){
				if(a*b*c == n) res ++;
			}
		}
	}
	cout << res << endl;
	return 0;
}

答案：2430

E:路径

分析：
这题考察的最短路算法啦，首先无意得先处理两点间距离问题。根据题意，敲敲处理即可。
当时图个省事，处理完距离问题后，直接上的三重循环的floyd算法，啪啪打脸，运行不出来，最后用的Dijkstra。

#include 
#include 
#include 
using namespace std;
const int Inf = 0x3f3f3f3f;
int arr[2050][2050];
int dis[2050]; //存储距离
int book[2050]; //标记数组 


int gcd(int i, int j){
	return i % j == 0 ? j : gcd(j, i % j);
}

void dijkstra(){
	memset(dis, 0x3f, sizeof(dis));
	dis[1] = 0;
	for(int i = 1; i <= 2021; i ++){
		int t = -1;
		for(int j = 1; j <= 2021; j ++){
			if(book[j] == 0 && (t == -1 || dis[t] > dis[j])) t = j;
		}
		if(t == -1) break;
		book[t] = 1;
		for(int j = 1; j <= 2021; j ++){
			dis[j] = min(dis[j], dis[t] + arr[t][j]);
		}
	}
} 

int main(void){
	for(int i = 2021; i > 0; i --){
		for(int j = i; j > 0; j --){
			if(i - j > 21){
				arr[i][j] = arr[j][i] = Inf;
			} else{
				arr[i][j] = arr[j][i] = i / gcd(i, j) * j;
			}
		}
	}
	dijkstra();
	cout << dis[2021];
	return 0;
}

答案：10266837

F：时间显示

给定的时间均不超过10^18次方的正整数

分析

1. 首先进行自我抨击，emmmm，我当时连1s = 1000ms,都是由样例推出来的（我还是比较纳闷，1小时等于60分钟，一分钟等于60s，为何1s = 1000ms，而不是60ms）,见笑了见笑了。。
2. 如果还是要强调的话，那便是格式化输出吧。printf("%02d:%02d:%02d\n", hh, mit, sec); 保证了均以两位输出，不足两位在数字前补上0.

#include 
#include 
using namespace std;
int main(void){
	long long sum;
	cin >> sum;
	sum /= 1000;//得出有多少秒 
//我们想要的只是这一天的时间表示，
//那必然总毫秒数应该小于24小时*60*60一天的总秒数 
	sum %= (24 * 60 * 60);
	int hh = sum / (60 * 60);
	sum -= (hh * 60 * 60);
	int mit = sum / 60;
	sum -= (mit * 60);
	int sec =  sum % 60;
	printf("%02d:%02d:%02d\n", hh, mit, sec);
	return 0;
}

G:砝码称重

分析：

1. 当时想着双重循环，一左一右，再加一个map记录所有的数量，最后输出map大小即可。。是啊，想法不成熟，两重循环，如何记录？双指针等在我脑子里砰砰乱跳，然而并没什么卵用。。实际上，这道题咔嚓考察的为动态规划。

2. 我们认为放左边为正数，不放为0，放右边为负数，每种砝码三种选择。本质为有限制的选择问题(背包问题)

3. 状态表示：f[i][j]表示，只从前i个物品中选，总重量为j的所有方案的集合，我们在意的是这个值是否为1【即属性值是否为为bool值】

4. 状态计算：f[i][j]可以由三部分构成不选w[i]（对应的为f[i-1][j]）, 选wi, 选-w[i] (放在天平右边)（对应的f[i-1][j+w[i]] 上述三种只要有一种为1，f[i][j]便为1.
   建议大家把这些状态带入定义中，便会有种豁然开朗的feel。
   设我们的输入的砝码总重量为m，最后答案便是，f[n][1到m]有多少个1即可。

5. 代码中需要考虑的一个小细节：当我们把所有砝码放在天平右边时，根据上述所说，对应的应该为-m,而我们的下标不能为负，所以加上一个偏移量，为砝码最大总重量。

#include 
#include 
using namespace std;
const int N = 200010, B = N/ 2;
int n, m;
int w[N];
int f[110][N];
int main(void){
	cin >> n;
	for(int i = 1; i <= n; i ++){
		cin >> w[i];
		m += w[i]; 
	}
	f[0][B] = 1;
	for(int i = 1; i <= n; i ++){
		for(int j = -m; j <= m; j ++){
			f[i][j + B] = f[i - 1][j + B];
			if(j - w[i] >= -m) f[i][j + B] |= f[i - 1][j - w[i] + B];
			if(j + w[i] <= m) f[i][j + B] |= f[i - 1][j + w[i] + B]; 
		}
	}
	int res = 0;
	for(int j = 1; j <= m; j ++){
		if(f[n][j + B]) res ++;
	}
	cout << res;
	return 0;
}

H：杨辉三角形

对于20%的评测样例，1<=N<=10;
对于所有测评样例，1 <= N ≤ 1000000000.

分析

1. 对于杨辉三角，我们一贯的作风便是使用数组模拟，但是此题数据范围过大，使用数组会溢出，据了解，当设置的数组太大不合理时，编译失败，直接0分处理。当时我最后做的这道题,想到每行都比上一行多一个数，直接把二维数组转换成对应的一维数组，感觉很是麻烦，并且时间也不够，但依旧满足不了所有样例需要，直接枚举的1-20中的位置，悄悄的得了20%的分数。。。sure， 我还懵了一个奇偶数的规律，，，菜的也是十分安详了。。。
2. 嗯，这道题是一个规律题。

（1）左右对称，我们找第一个出现的数，且从左往右找，因此我们只看左半部即可。

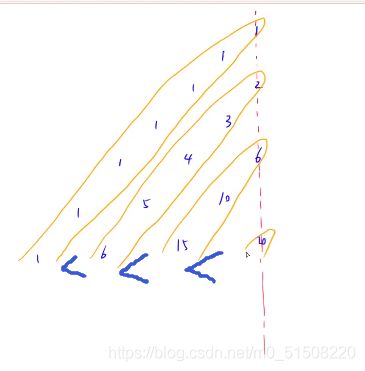
我们看没一斜行，从上至下依次递增，同一水平行从左往右依次递增。
我们找指定数n第一次出现的位置时，应该从最下面的斜行开始找，只有这样才能保证改行的水平行左边都小于它，上边的小于它，他是该数第一次出现的地方。
发现每个斜行的起始数字规律如下：

当n=17时，对应的斜线第一个数>10^9（改斜线上的每一个数均大于10^9,已经超过需要求得数据范围啦）;
当n=16时，对应的斜线的第一个数<10^9,所以，n=16即可。我们枚举时只需要从第16斜行开始枚举即可。枚举得每一斜行（单调递增），通过二分查找来判断目标值是否在这一斜行。
（2）如何二分？如图所示。

每条斜线的数字都可用组合数表示出来，发现，第k个斜行的都是有规律的C(n, k), n是逐渐递增的。我们找到的每条斜线是第一个>=目标值的位置，判断是不是目标值，若不是，则查找上一斜行。

（3）最后答案：当我们找出查找目标值在对应的组合数表示为C(r, k), 表示该位置上有r行，（可以发现每行的数字个数是递增的），左边有k个数，我们计算的是第几个数（若是对应到数组中，下标应该从1开始）
答案：r*(r+1)/2+k+1

#include 
#include 
using namespace std;
typedef long long LL;
int n;
//定义一个求组合数的函数（每个斜线的第一个数） 
LL C(int a, int b){
	LL res = 1;
	for(int i = a, j = 1; j <= b; i --, j ++){
		res = res * i / j;
		if(res > n) return res; //放置爆 long long 
	}
	return res;
} 

bool check(int k){
	LL l = k * 2,  r = n; //下限是2 *k, 上限是n
	while(l < r){
		LL mid = l + r >> 1;
		if(C(mid, k) >= n) r = mid;
		else l = mid + 1;
	} 
	if(C(r, k) != n) return false;
	
	cout << r * (r + 1) / 2 + k + 1;
	return true;
}
int main(void){
	cin >> n;
	if(n == 1){
		cout << 1 << endl;
		return 0;
	}
	for(int k = 16; ; k --){
		if(check(k)){
			break;
		}
	}
	return 0;
} 

I：双向排序

分析：

1. 最简单粗暴的写法，便是对于每个输入均以sort处理，显然，对于数据量过大的会超时，但会得点分。。
2. 其实，我们很容易想到，当我们需要排序的次数很多时，难免会有几段序列不用排序却反复处理了，但具体细节的处理以及代码的落实就不是轻飘飘的几句话就可以的。
3. 我们简单的概括一下题意：一共两个操作（1-n）的排列，将某前缀降序排列，将某后缀升序。共m个操作。
   （1）对于连续的降序或升序操作，我们保留最长的一个操作即可。有效操作必然是左右交替的
   （2）我们本来输入的序列就是升序的，第一个有效操作必然是降序操作
   （3）当左侧区间长度大于上一个对左端操作时，含重复操作的区间了，我们只需要操作后一个（长度范围更大的）左区间操作即可。如下图所示：1、2操作可省去。
   
   字有些丑，行大事者不拘小节
   如果前缀操作的长度比上一个前缀操作的区间更大的话，被包含的左操作及与其对应的后缀操作可删掉。
   更加具体点说的话，我们的左操作、右操作在严格变小。每次操作，都是将（两次反转区间）的交集反转。当交集为空的话，便是填满了整个序列。

关于代码：

1. 我们用一个pair来存，第一个参数表示具体哪个操作，第二个参数表示下标
2. 具体细节可参见代码中注释

#include 
#include 
#include 
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n, m;
PII stk[N];
int ans[N];
int main(void){
    cin >> n >> m;
    int top = 0;
    while(m --){
        int p, q;
        scanf("%d%d",&p, &q);
        if(!p){ //前缀操作
        //两个连续的左操作
            while(top && stk[top].x == 0) q = max(q, stk[top --].y);
        //删掉前边比当前操作小的左端操作及其对应的右端操作
            while(top >= 2 && stk[top - 1].y <= q) top -= 2;
            stk[++ top] = {0, q};
        } 
        else if(top){ //当第一个操作为右端操作时，没有必要处理
            while(top && stk[top].x == 1) q = min(q, stk[top --].y);
            while(top >= 2 && stk[top - 1].y >= q) top -= 2;
            stk[++ top] = {1, q};
        }    
    }
    int k = n, l = 1, r = n;
//从前往后遍历所有操作
    for(int i = 1; i <= top; i ++){
        //第一个操作为前缀降序操作，该区间右端的数是可以固定的了。
        if(stk[i].x == 0)
            while(r > stk[i].y && l <= r) ans[r --] = k --;
        else
            while(l < stk[i].y && l <= r) ans[l ++] = k --;
        if(l > r) break;
    }
    if(top % 2){ //做完了右区间，还剩一个左区间。
        //剩下的左区间操作为降序，我们从左边开始填。
        while(l <= r) ans[l ++] = k --;
    } else{
        while(l <= r) ans[r --] = k --;
    }
    for(int i = 1; i <= n; i ++){
        printf("%d ", ans[i]);
    }
    return 0;
}

J：括号序列

分析：

1. 首先进行自我抨击，，呜呜呜呜呜。。也是菜的不行不行了。。我当时不成熟的思路是这样的，输入的一段序列计算出左右括号的差，这便是最少需要插入的个数了，然后进行搜索，对于每个插完指定位数的序列，进行括号是否配对检验，即写一个check函数（栈的应用嘛），然后ans++； 啪啪打脸，写出一个死循环不说，像这种序列)))(((计算出的差为0，是不是就不需要插入括号了？！ 想法很是幼稚。。

2. 慌的一批，这题咔嚓的是动态规划。。。且听我慢慢道来

3. 一个合法括号序列满足：左右括号数量相同 和任何一个前缀中，左括号数量不小于右括号数

4. 我们不会同时添加一对左右括号，因为在一个合法括号配对序列中，去掉某对括号，剩下的还是合法的、配对的。因此，我们添加左右括号是独立的。

5. 从前往后扫描，当前左括号比右括号多几个，当cnt小于0时，我们必须添加一个左括号cnt=0，最后添加的右括号数量=cnt，添加的左括号可用一个另变量存储。两个相加，就是最少添加的括号数量。

6. 方案数可以独立来看，先添加左括号，再添加右括号。左括号最少添加数量对应的方案数，右括号最少添加数量的方案数相乘即可。（我们考虑左右括号添加是否会有干扰，当添加的位置（相对原序列而言）在同一个空隙里添加左括号、右括号，一定是))((右括号在前，左括号在右； 因为如果是()左括号在前右括号在右，这就是一对匹配的括号，当我们去掉这一对时，不会有影响，但把原序列变成合法后插入的括号数就不是最少的了， 因此左右括号插入是独立的）

7. 如果只添加左括号，如何保证不重复呢？将序列按照右括号分割可以分成若干段，每段而言，不同的便是左括号的数量。最后一段内一定不会加左括号,因为最后一段满足cnt>0
   ，因此我们在添加左括号的时候，规定只能在右括号前添加左括号，这样就能保证不重复。

8. 状态表示：f[i][j] 表示只考虑前i个括号，左括号比右括号多j个的所有方案的集合。f[i][j] = k k表示方案数量

9. 保证添加的括号数最少，f[n][0]...f[n][n]一直枚举即可 。左括号比右括号最多多n个嘛。一定至少会有一个非空集合。

10. 状态计算：
    (1)f[i][j]当前是左括号s[i]=’(’, f[i][j] = f[i - 1][j - 1]
    (2)当前是右括号，可以考虑往这个右括号前面加左括号，可以是0-j+1个（根据定义，左括号比右括号多j个，这个位置又是一个右括号所以需要再+1，嘛），f[i][j] = f[i - 1][j + 1] + f[i-1][j] + f[i-1][j - 1] .... + f[i-1][0] 类似于完全背包，f[i][j - 1] = f[i - 1][j] + f[i-1][j - 1] + ...f[i-1][0] 所以：f[i][j] = f[i][j-1] + f[i - 1][j+1]

#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int N = 5010, MOD = 1e9 + 7;
int n;
char str[N];
int f[N][N];
LL calc(){
    memset(f, 0, sizeof(f));
    f[0][0] = 1;
    for(int i = 1; i <= n; i ++){
        if(str[i] == '(') {
            for(int j = 1; j <= n; j ++){
                f[i][j] = f[i-1][j-1];
            }
        } else{
            f[i][0] = (f[i-1][0] + f[i-1][1]) % MOD;
            for(int j = 1; j <= n; j ++){
                f[i][j] = (f[i - 1][j + 1] + f[i][j - 1]) % MOD;
            }
        }
    }
    for(int i = 0; i <= n; i ++){
        if(f[n][i]) return f[n][i];
    }
    return -1;
}

int main(void){
    scanf("%s", str+1);
    n = strlen(str+1);
    LL l = calc();//左括号的做法
    reverse(str + 1, str+n+1);
    //右括号的做法，将整个序列反转，左括号变成右括号，调用相同函数即可。
    for(int i = 1; i <= n; i ++){
        if(str[i] == '(') str[i] = ')';
        else str[i] = '(';
    }   
    LL r = calc();
    printf("%lld", l * r % MOD);
    return 0;
}