点对于某个对称轴镜像翻转,这里用二维演示,思路及核心方法都是一致的,二维能较好说明。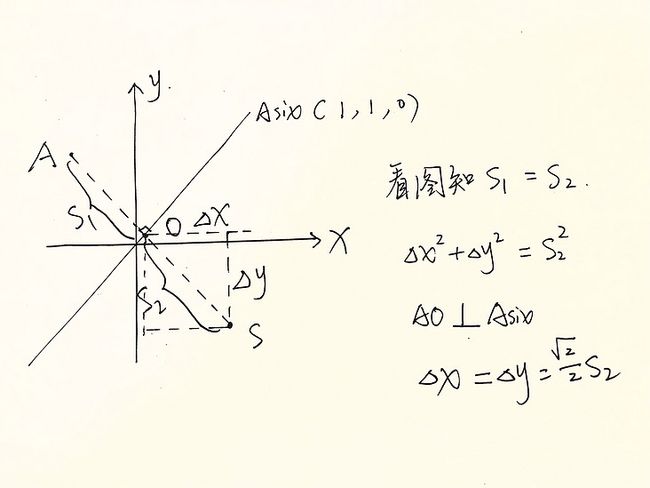
找到在对称轴上与点最近的点
// 将对称轴整成线段
const line = new THREE.Line3(axis, new THREE.Vector3(0, 0, 0))
const linePoint = new THREE.Vector3()
line.closestPointToPoint(arr[i], false, linePoint)
// linePOint就是arr[i]点在线段上最近的点得出点与线段上的点的距离S1
// linePoint是线段上的点 vec3是需要翻转的点
const distance = linePoint.distanceTo(vec3)按方向延长S1的距离至S点
// 简单的勾股定理
const p = Math.sqrt(2) * 0.5
x = linePoint.x + p * distance
y = linePoint.y - p * distance需要进行判断
对于上方的结果只是点在对称轴左侧才成立, 需要判断点的方位
/**
* 判断是否在左侧
* 因为数据是否在左右侧关系到xy的符号问题, 距离是没有负数的,而坐标是存在正负的
*/
function leftORRight() {
let left = true;
const line = new THREE.Line3(axis, new THREE.Vector3(0, 0, 0))
const linePoint = new THREE.Vector3()
for (let i = 0; i < arr.length; i++) {
line.closestPointToPoint(arr[i], false, linePoint)
if (linePoint.x < arr[i].x) {
// 右侧
left = false;
break;
}
}
return left;
}All Code
import * as THREE from 'three'
/**
* 实现点绕制定对称轴镜像转换的功能
*/
function axisRound(scene) {
// const arr = [
// new THREE.Vector3(-1, 1, 0),
// new THREE.Vector3(-2, -1, 0),
// new THREE.Vector3(-1, -1, 0),
// new THREE.Vector3(-1, 2, 0),
// ]
// 提供测试的数据
const arr = [
new THREE.Vector3(1, -1, 0),
new THREE.Vector3(2, -1, 0),
new THREE.Vector3(1, 1, 0),
new THREE.Vector3(1, -2, 0),
]
const material = new THREE.MeshBasicMaterial({ color: 'red', side: THREE.DoubleSide });
arr.forEach(row => {
const geometry = new THREE.PlaneGeometry(0.5, 0.5);
const plane = new THREE.Mesh(geometry, material);
scene.add(plane);
plane.position.set(row.x, row.y, row.z)
})
const axis = new THREE.Vector3(1, 1, 0)
{
const points = [];
points.push(axis);
points.push(new THREE.Vector3(-10, -10, 0))
points.push(new THREE.Vector3(10, 10, 0))
const geometry = new THREE.BufferGeometry().setFromPoints(points);
const line = new THREE.Line(geometry, material);
scene.add(line);
}
arr.forEach(row => {
const geometry = new THREE.PlaneGeometry(0.5, 0.5);
const plane = new THREE.Mesh(geometry, material);
scene.add(plane);
const n = t(row, axis)
console.log(n);
plane.position.set(n.x, n.y, n.z)
})
// 正式开始计算
function t(vec3, axis) {
const line = new THREE.Line3(axis, new THREE.Vector3(0, 0, 0))
const linePoint = new THREE.Vector3()
line.closestPointToPoint(vec3, false, linePoint)
// 得出2的算术平方根的1/2
const p = Math.sqrt(2) * 0.5
const distance = linePoint.distanceTo(vec3)
let x, y;
if (leftORRight()) {
x = linePoint.x + p * distance
y = linePoint.y - p * distance
} else {
x = linePoint.x - p * distance
y = linePoint.y + p * distance
}
return new THREE.Vector3(x, y, 0)
}
/**
* 判断是否在左侧
* 因为数据是否在左右侧关系到xy的符号问题, 距离是没有负数的,而坐标是存在正负的
*/
function leftORRight() {
let left = true;
const line = new THREE.Line3(axis, new THREE.Vector3(0, 0, 0))
const linePoint = new THREE.Vector3()
for (let i = 0; i < arr.length; i++) {
line.closestPointToPoint(arr[i], false, linePoint)
if (linePoint.x < arr[i].x) {
// 右侧
left = false;
break;
}
}
return left;
}
}
export { axisRound }