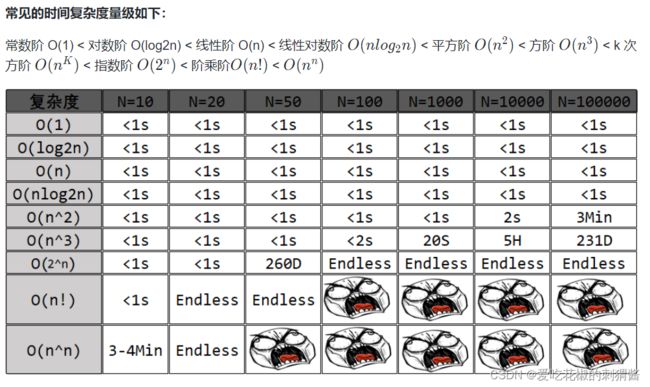
2022年(第13届蓝桥杯省赛)Python 14 天夺奖冲刺营
2022年(第13届蓝桥杯省赛)Python 14 天夺奖冲刺营
2022.03.25
攒了一周的视频直播没有看,更新完了直接看合集。
数据结构基础之链表篇
什么是链表
链表是线性表的链式存取的数据结构,是一种链式存取的数据结构,是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:数据域(数据元素的映象)+ 指针域(指示后继元素存储位置),数据域就是存储数据的存储单元,指针域就是连接每个结点的地址数据。 相比于线性表顺序结构,操作复杂。
class Node:
def __init__(self, value, next=None):
self.value = value
self.next = next
def createLink():
root = Node(0)
tmp = root
for i in range(1, 11 ):
tmp.next = Node(i)
tmp = tmp.next
tmp.next = None
return root
def insert(x, linkedroot):
tmp = Node(x)
tmp.next = root.next
root.next = tmp
def delete(x, root):
tmp = tmp1 = root
while tmp != None:
if tmp.value == x:
tmp1.next = tmp.next
tmp1 = tmp
tmp = tmp.next
def show(root):
tmp = root.next
while tmp.next != None:
print(tmp.value, end=" ")
tmp = tmp.next
print("")
if __name__ == '__main__':
n = int(input())
root = createLink()
# show(root)
for i in range(n):
x = int(input())
delete(x, root)
insert(x, root)
show(root)
# -*- coding: utf-8 -*-
"""
Created on Fri Mar 25 10:31:31 2022
@author: hasee
"""
class Node:
def __init__(self, value, next=None):
self.value = value
self.next = next
def createLink():
root = Node(0)
tmp = root
for i in range(1, 11 ):
tmp.next = Node(i)
tmp = tmp.next
tmp.next = None
return root
def insert(x, linkedroot):
tmp = Node(x)
tmp.next = root.next
root.next = tmp
def delete(x, root):
tmp = tmp1 = root
while tmp != None:
if tmp.value == x:
tmp1.next = tmp.next
tmp1 = tmp
tmp = tmp.next
def show(root):
tmp = root.next
while tmp.next != None:
print(tmp.value, end=" ")
tmp = tmp.next
print("")
if __name__ == '__main__':
n = int(input())
root = createLink()
# show(root)
for i in range(n):
x = int(input())
delete(x, root)
insert(x, root)
show(root)
# 用列表模拟单链表
ls=[i for i in range(1,11)]
m = int(input())
ns = [int(input()) for i in range(m)]
cnt = 0
for i in ns:
ls.remove(i)
ls.insert(0,i)
for j in ls:
print(j,end=" ")
print()
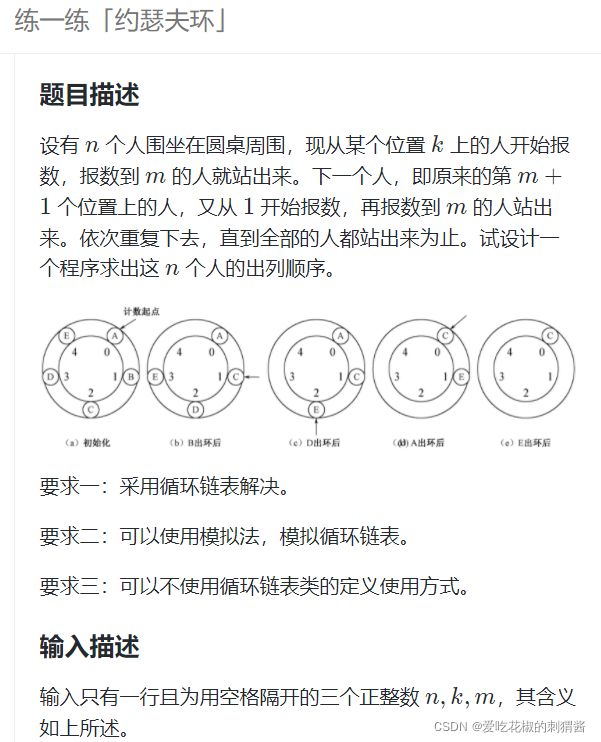
n,k,m = map(int, input().split())
def josephus(num, k, m):
alist = list(range(1, num + 1))
index, step = k - 1, m # 从k号开始报数,数到m的那个人出列
for i in range(num-1):
index = (index + step - 1) % len(alist)
print(alist.pop(index))
return ('{}'.format(alist[0]))
print(josephus(n, k, m))
class Node():
def __init__(self, value, next=None):
self.value = value
self.next = next
def createLink(n):
if n <= 0:
return False
if n == 1:
return Node(1)
else:
root = Node(1)
tmp = root
for i in range(2, n + 1):
tmp.next = Node(i)
tmp = tmp.next
tmp.next = root
return root
if __name__ == '__main__':
n, k, m = map(int, input().split())
root = createLink(n)
tmp = root
for i in range(0, k - 1):
tmp = tmp.next
while tmp.next != tmp:
for i in range(m - 2):
tmp = tmp.next
print(tmp.next.value, " ")
tmp.next = tmp.next.next
tmp = tmp.next
print(tmp.value)
class Node:
def __init__(self, value, next=None):
self.value = value
self.next = next
def createLink():
root = Node(0)
tmp = root
for i in range(10):
tmp.next = Node(i+1)
tmp = tmp.next
tmp.next = None
return root
def insert(x, linkedroot):
tmp = Node(x)
tmp.next = root.next
root.next = tmp
def delete(x, root):
tmp = tmp1 = root
while tmp != None:
if tmp.value == x:
tmp1.next = tmp.next
tmp1 = tmp
tmp = tmp.next
def show(root):
tmp = root.next
while tmp != None:
print(tmp.value, end=" ")
tmp = tmp.next
print("")
if __name__ == '__main__':
n = int(input())
root = createLink()
# show(root)
for i in range(n):
x = int(input())
delete(x, root)
insert(x, root)
show(root)
数据结构基础之队列篇
什么是队列
如果说链表和顺序表是对数据的存取位置的组织方式,那么队列就是一种对于存取方式限制的组织方式。换一种方式描述的话就是,队列既可以采用链表来表示,也可以采用数组(线性表)来表示,我们限制的是对于存放数据的存取方式。
队列的逻辑结构
队列:只允许在一端进行插入操作,而另一端进行删除操作的线性表。
空队列:不含任何数据元素的队列。
允许插入(也称入队、进队)的一端称为队尾,允许删除(也称出队)的一端称为队头。
from collections import deque
V = deque()#会员窗口
N = deque()#普通窗口
M = int(input())
while M > 0:
M -= 1
op = input().split()
# print(op[0])
if op[0] == 'IN':
if op[2] == "V":
V.append(op[1])
else:
N.append(op[1])
else:
if op[1] == "V":
V.popleft()
else:
N.popleft()
while V:
print(V.popleft())
while N:
print(N.popleft())
Vqueue = []
Vhead = 0
Vtail = 0
Nqueue = []
Nhead = 0
Ntail = 0
def inque(name, type):
global Vhead, Vtail, Nhead, Ntail,Vqueue ,Nqueue
if (type == 'V'):
Vqueue.append(name)
Vtail += 1
else:
Nqueue.append(name)
Ntail += 1
# print(Vqueue)
def getHead(type):
global Vhead, Vtail, Nhead, Ntail,Vqueue ,Nqueue
if (type == 'V'):
# print(Vhead)
return Vqueue[Vhead]
else:
# print(Nhead)
return Nqueue[Nhead]
def outque(type):
global Vhead, Vtail, Nhead, Ntail,Vqueue ,Nqueue
if (type == 'V'):
if (Vhead == Vtail):
return None
else:
s = getHead(type)
Vhead += 1
return s
else:
if (Nhead == Ntail):
return None
else:
s= getHead(type)
Nhead += 1
return s
if __name__ == '__main__':
M = 0
M = int(input())
while M > 0:
M -= 1
op = input().split()
# print(op[0])
if op[0] == 'IN':
inque(op[1], op[2])
# print('in')
else:
outque(op[1])
# print('out')
# print("VVVVV",Vqueue)
# print("NNNN",Nqueue)
# print(M)
s = outque('V')
while s!=None:
print(s)
s = outque('V')
s = outque('N')
while s != None:
print(s)
s = outque('N')
Vqueue = []
Nqueue = []
def inque(name, type):
global Vqueue ,Nqueue
if (type == 'V'):
Vqueue.append(name)
else:
Nqueue.append(name)
def outque(type):
global Vqueue ,Nqueue
if (type == 'V'):
if(len(Vqueue)==0):
return None
else:
s=Vqueue[0]
Vqueue.remove(Vqueue[0])
return s
else:
if (len(Nqueue)==0):
return None
else:
s = Nqueue[0]
Nqueue.remove(Nqueue[0])
return s
if __name__ == '__main__':
M = 0
M = int(input())
while M > 0:
M -= 1
op = input().split()
# print(op[0])
if op[0] == 'IN':
inque(op[1], op[2])
# print('in')
else:
outque(op[1])
# print('out')
# print("VVVVV",Vqueue)
# print("NNNN",Nqueue)
# print(M)
s = outque('V')
while s!=None:
print(s)
s = outque('V')
s = outque('N')
while s != None:
print(s)
s = outque('N')
数据结构基础-栈
# deque 既可以用作队列,也可以用作栈
# 2022.04.05临近蓝桥杯的比赛,一直提示测试失败,样例都能通过。欢迎在评论区讨论。
from collections import deque
q = deque() # 栈q
n = int(input())
while n:
n -= 1
op = input().split()
if op[0] == 'in':
q.append(op[1])
else:
while q and q[-1]!= op[1]: # 不能用q.pop()来判断,他会直接把最后一个元素弹出去
q.pop()
if q:
print(q.pop())
else:
print('Empty')
MyStack=[]
Top=-1
def inStack(name):
global Top,MyStack
MyStack.append(name) #使用python不需要考虑是否够用
Top+=1
def isEmpty():
global MyStack
if(len(MyStack)==0):
return True
else:
return False
def getTop():
global Top,MyStack
if(isEmpty()):
return ""
else:
return MyStack[Top]
def outStack():
global Top,MyStack
if(isEmpty()):
return False
else :
del MyStack[Top]
Top-=1
return True
if __name__=='__main__':
N=0
N=int (input())
while N>0:
N-=1
op=input().split()
if(op[0]=='in'):
inStack(op[1])
else :
while(getTop()!=op[1]):
outStack()
outStack()
if(isEmpty()) :
print("Empty")
else:
print(getTop())
class MyStack:
def __init__(self):
self._data = [] # 使用list存储栈元素
def is_empty(self):
return self._data == []
def push(self, elem):
self._data.append(elem)
def pop(self):
if self._data == []:
raise Warning ("此栈为空,错误操作");
return self._data.pop()
def top(self):
if self._data == []:
raise Warning("此栈为空,错误操作");
return self._data[-1]
if __name__=='__main__':
N=int (input())
Stack =MyStack()
while N>0:
N-=1
op=input().split()
if(op[0]=='in'):
Stack.push(op[1])
else :
while(Stack.top()!=op[1]):
Stack.pop()
Stack.pop()
if(Stack.is_empty()) :
print("Empty")
else:
print(Stack.top())
数据结构基础-散列表(Hash)
判断现有数据集合中是否有这个元素,或者是否有满足条件的元素。
其中的 Hash 算法则可以帮助我们判断是否有这个元素,虽然功能简单,但是其 O(1) 时间复杂度是具有高性能的。通过在记录的存储地址和它的关键码之间建立一个确定的对应关系。这样,不经过比较,一次读取就能得到所查元素的查找方法。相比普通的查找算法来说,仅仅在比较的环节,就会大大减少查找或映射所需要的时间。
h = 999983
Value = ['']*h
UpValue = ['']*h
UpValueCount = 0
def isAt (s):
n = int (hash(s)+h)%h
# print(n)
if Value[n] == '':
return False
elif Value[n]==s:
return True
else:
for i in range(0,UpValueCount):
if UpValue[i] == s:
return True
return False
def ins (s):
global UpValueCount
n =int (hash(s)+h)%h
if Value[n] == '':
Value[n]=s
return True
elif Value[n]==s:
return False
else:
for i in range(0,UpValueCount):
if UpValue[i] == s:
return False
UpValue[UpValueCount] = s
UpValueCount=UpValueCount+1
return True
if __name__=='__main__':
N=int (input())
ans = 'NO'
flag = False
while N>0:
N-=1
word=input()
# print(word)
if(not(flag)) :
if(isAt(word)):
flag=True
ans=word
else:
ins(word)
print(ans)
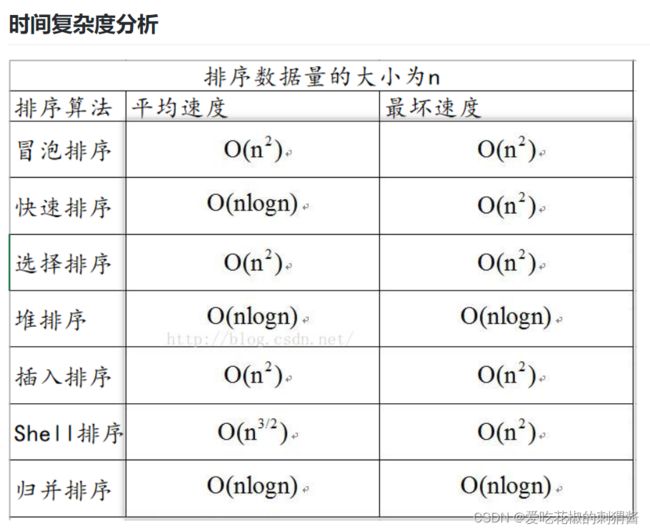
数据结构之排序算法
- 选择排序
基本思想
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,按照顺序放在待排序的数列的最前,直到全部待排序的数据元素排完。
def selection_sort(a):
n = len(a)
for i in range(n - 1):
k = i
for j in range(i + 1, n):
if a[j] < a[k]:
k = j
if k != i:
temp = a[i]
a[i] = a[k]
a[k] = temp
arr = [5 ,4 ,6 ,8 ,7, 1, 2 ,3]
selection_sort(arr)
print(arr)
- 冒泡排序
基本思想
所谓冒泡排序就是依次将两个相邻的数进行比较,大的在前面,小的在后面。 - 即先比较第一个数和第二个数,大数在前,小数在后,然后比较第 2 个数和第 3 个数,直到比较最后两个数
- 第一趟排序结束后,最小数的数一定在最后
- 第二趟排序在第一趟的基础上重复上述操作
由于排序过程中总是大数在前,小数在后,相当于气泡上升,所以叫冒泡排序。
- 大数在前,小数在后排序后得到的是降序
- 小数在前,大数在后排序后得到的是升序结果
def BubbleSort(arr):
n = len(arr)
for i in range(n-1): # 遍历所有数组元素
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
arr = [4, 5, 6, 1, 2, 3]
BubbleSort(arr)
print(arr)
- 桶排序
基本思想
桶排序的思想是,若待排序的记录的关键字在一个明显有限范围内时,可设计有限个有序桶,每个桶只能装与之对应的值,顺序输出各桶的值,将得到有序的序列。简单来说,在我们可以确定需要排列的数组的范围时,可以生成该数值范围内有限个桶去对应数组中的数,然后我们将扫描的数值放入匹配的桶里的行为,可以看作是分类,在分类完成后,我们需要依次按照桶的顺序输出桶内存放的数值,这样就完成了桶排序。
maxN = 10 #题目出现的数据的最大值
b={0:0,1:0,2:0,3:0,4:0,5:0,6:0,7:0,8:0,9:0}
n=eval(input("输入整数n"))
for i in range(n):
x=eval(input("输入0~9之间的整数"))
b[x]+=1
for key in range(maxN):
while b[key]>0:
print(key,end=' ')
b[key]-=1
- 插入排序
基本思想
插入排序是一种简单的排序方法,时间复杂度为 O(n*n),适用于数据已经排好序,插入一个新数据的情况。其算法的基本思想是,假设待排序的数据存放在数组 a[1…n] 中,增加一个节点 x 用于保存当前数据,进行比较,a[1]即作为有序区,a[2…n] 作为无序区。
def insertionSort(arr):
for i in range(1, len(arr)):
x = arr[i]
j = i - 1
while j >= 0 and x < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = x
arr = [0, 3, 2, 4, 1, 6, 5, 2, 7]
insertionSort(arr)
print(arr)
- 希尔排序
基本思想
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法,同时也突破了之前内排序算法复杂度为 O(n2)的限制。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率.
- 插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
a = [56,52,-96,-53,23,-789,520] #测试案例
b = len(a) #列表长度
gap = b // 2 #初始步长设置为总长度的一半
while gap >= 1:
for i in range (b):
j = i
while j>=gap and a[j-gap] > a[j]: #在每一组里面进行直接插入排序
a[j],a[j-gap] = a[j-gap],a[j]
j-= gap
gap=gap//2 #更新步长
print(a)
- 快速排序
基本思想
快速排序是一种采用分治法解决问题的一个典型应用,也是冒泡排序的一种改进。它的基本思想是,通过一轮排序将待排记录分割成独立的两部分,其中一部分均比另一部分小,则可分别对这两部分继续进行排序,已达到整个序列有序。排序的时间复杂度为 O(nlogn),相比于简单排序算法,运算效率大大提高。
算法步骤
- 从序列中取出一个数作为中轴数;
- 将比这个数大的数放到它的右边,小于或等于他的数放到它的左边;
- 再对左右区间重复第二步,直到各区间只有一个数。
def qsort(l,r):
if(l>r):
return None
tmp=a[l]
i=l
j=r
while i!=j:
while(a[j]>=tmp and j>i):
j-=1
while(a[i]<=tmp and j>i):
i+=1
if(j>i):
t=a[i]
a[i]=a[j]
a[j]=t
a[l]=a[i]
a[i]=tmp
qsort(l,i-1)
qsort(i+1,r)
- 归并排序
基本思想
-
归并排序是由递归实现的,主要是分而治之的思想,也就是通过将问题分解成多个容易求解的局部性小问题来解开原本的问题的技巧。
-
归并排序在合并两个已排序数组时,如果遇到了相同的元素,只要保证前半部分数组优先于后半部分数组, 相同元素的顺序就不会颠倒。所以归并排序属于稳定的排序算法。
-
每次分别排左半边和右半边,不断递归调用自己,直到只有一个元素递归结束,开始回溯,调用 merge 函数,合并两个有序序列,再合并的时候每次给末尾追上一个最大 int 这样就不怕最后一位的数字不会被排序。
def MergeSort(lists):
if len(lists) <= 1:
return lists
num = int( len(lists) / 2 )
left = MergeSort(lists[:num])
right = MergeSort(lists[num:])
return Merge(left, right)
def Merge(left,right):
r, l=0, 0
result=[]
while l<len(left) and r<len(right):
if left[l] <= right[r]:
result.append(left[l])
l += 1
else:
result.append(right[r])
r += 1
result += list(left[l:])
result += list(right[r:])
return result
if __name__=='__main__':
a=[1, 2, 3, 4, 5, 6, 7, 90, 21, 23, 45]
a=MergeSort(a)
print (a)
N = int(input())
list1 = list(map(int, input().split()))
list1.sort()
for i in list1: # 输出list1,以空格为间隔
print(i, end = ' ')
print() # 换行输出
for i in range(N - 1, -1, -1): # 已经排好序直接倒着输出就是逆序了
print(list1[i], end=' ')
内置模板
Python 中的队列
from queue import Queue
## maxsize设置队列中,数据上限,小于或等于0则不限制,容器中大于这个数则阻塞,直到队列中的数据被消掉
q = Queue(maxsize=0)
成员函数:
-
Queue.qsize() 返回队列的大致大小。
-
Queue.empty() 如果队列为空,返回 True 否则返回 False
-
Queue.full() 如果队列是满的返回 True ,否则返回 False
-
Queue.put(item, block=True, timeout=None)
- 常用时忽略默认参数,即使用 Queue.put(item)。
- 将 item 放入队列,如果可选参数 block 是 true 并且 timeout 是 None (默认),则在必要时阻塞至有空闲插槽可用。
- 如果 timeout 是个正数,将最多阻塞 timeout 秒,如果在这段时间没有可用的空闲插槽,将引发 Full 异常。
- 反之 (block 是 false),如果空闲插槽立即可用,则把 item 放入队列,否则引发 Full 异常 ( 在这种情况下,timeout 将被忽略)。
-
Queue.get(block=True, timeout=None)
- 常用时忽略默认参数,即使用 Queue.get()。
- 从队列中移除并返回一个项目。如果可选参数 block 是 true 并且 timeout 是 None (默认值),则在必要时阻塞至项目可得到。
- 如果 timeout 是个正数,将最多阻塞 timeout 秒,如果在这段时间内项目不能得到,将引发 Empty 异常。反之 (block 是 false),如果一个项目立即可得到,则返回一个项目,否则引发 Empty 异常 (这种情况下,timeout 将被忽略)。
Python 字典
在 Python 中我们不叫映射,也不叫 map,我们称作字典。用法跟 Java 和 c++ 都是有一定区别的。
字典的创建
massege={'小李':'123124543643','xiaohua':'17855666','LiMing':'1249699859456'}
#或者创建空的字典
empty_dict = {}
#或者使用元组作为key
group_dict = {(60, 99):'good', 100:'nice'}
字典的添加
# 如果字典内不含有相应的Key值,则会执行添加操作
dict[key]=value
字典的修改
# 如果字典内含有相应的Key值,则会执行更新操作
dict[key]=new_value
# 使用update()修改
# update() 方法可使用一个字典所包含的 key-value 对来更新己有的字典。如果有就修改,没有就添加。
dict.update({'key':123,'key2':234})
字典的删除
del dict['key'] # 删除键是'key'的条目
dict.clear() # 清空字典所有条目
del dict # 删除字典
字典的访问
dict = {'Name': 'Zara', 'Age': '7'}
print (dict['Name'])
#当然如果key值不存在,将会抛出异常
#也可以是用get()方法,不存在会返回None,但不会抛出异常
print(dict.get('Name'))
city=[]
dig = [[] for i in range(1000)]
def find(s):
for i in range(0,len(city)):
if (city[i]==s):
return i
return -1
if __name__ == '__main__':
n=int (input())
for i in range(0,n):
d=input().split()
#print(d[1] )
flag=find(d[1])
if(flag==-1):
city.append(d[1])
dig[len(city)-1].append(d[0])
else:
dig[flag].append(d[0])
for i in range(0,len(city)):
print(city[i],len(dig[i]))
for j in range(0,len(dig[i])):
print(dig[i][j])
import queue
V = queue.Queue()
N = queue.Queue()
if __name__ == '__main__':
M = 0
M = int(input())
while M > 0:
M -= 1
op = input().split()
# print(op[0])
if op[0] == 'IN':
if op[2] == "V":
V.put(op[1])
else:
N.put(op[1])
else:
if op[1] == "V":
V.get()
else:
N.get()
# print('out')
# print("VVVVV",Vqueue)
# print("NNNN",Nqueue)
# print(M)
while not (V.empty()):
print(V.get())
while not (N.empty()):
print(N.get())
dict={}
if __name__=='__main__':
N=int (input())
ans = 'NO'
flag = False
while N>0:
N-=1
word=input()
if(not(flag)) :
if(dict.get(word)!=None):
flag=True
ans=word
else:
dict[word]=True
print(ans)
打表法和模拟法
'''
def check(a, b, c):
flag = []
flag.append(0)
while (a != 0):
if (a % 10 in flag):
return False;
else:
flag.append(a % 10)
if (b % 10 in flag):
return False;
else:
flag.append(b % 10)
if (c % 10 in flag):
return False;
else:
flag.append(c % 10)
a = (int) (a / 10)
b =(int) (b / 10)
c = (int) (c / 10)
# print(flag)
return True
if __name__ == '__main__':
ans = 0
for a in range(123, 987):
for b in range(123, 987 - a):
c = a + b
if (check(a, b, c)):
ans += 1
print(a, "+", b, " = ", c)
print(ans)
'''
print(336) # 填空题只用输出最终结果就可以了
'''
import time
def cnt(a):
ans=0
for j in range(1,a+1):
if a%j ==0:
ans+=1
return ans
start = time.time()
if __name__ == '__main__':
for i in range(1,400000):
if cnt(i)==100:
print(cnt(i),' ',i)
break
end = time.time()
print(start - end)
'''
print(45360) # 将最终结果输出
Python 跑的是真的慢,等了好长的时间。

复杂度是 n \sqrt{n} n
def cnt1(a):
ans = 0
for i in range(1, int(a ** 0.5) + 1):
if a % i == 0:
ans += 2
return ans
for i in range(1, 45361):
if cnt1(i) == 100:
print(cnt1(i),' ',i)
break
'''
def gcd(a, b):
tem = 0
while (b > 0):
temp = b
b = a % b
a = temp
return a
if __name__ == '__main__':
ans=0
for a in range(1, 2021):
for b in range(1, 2021):
if gcd(a,b)==1 :
ans+=1
print( ans)
'''
print(2481215)
# 用python自带math求最大公约数
import math
ans = 0
for a in range(1, 2020 + 1):
for b in range(1, 2020 + 1):
if math.gcd(a, b) == 1:
ans += 1
print(ans)
- 「天干地支」
tg = ["geng", "xin", "ren", "gui", "jia", "yi", "bing", "ding", "wu", "ji"]
dz = ["shen", "you", "xu", "hai", "zi", "chou",
"yin", "mou", "chen", "si", "wu", "wei"]
if __name__ == '__main__':
year = int(input())
print(tg[year % 10], dz[year % 12], sep='')
递推法与递归法
递推算法解题的基本思路:
- 将复杂计算转换为简单重复运算;
- 通过找到递推关系式进行简化运算;
- 利用计算机的特性,减少运行时间。
递推算法的一般步骤:
- 根据题目确定数据项,并找到符合要求的递推关系式;
- 根据递推关系式设计递推程序;
- 根据题目找到递推的终点;
- 单次查询可以不进行存储,多次查询都要进行存储;
- 按要求输出答案即可。
递归算法的思想:
- 将复杂计算过程转换为简单重复子过程;
- 找到递归公式,即能够将大问题转化为小问题的公式;
- 自上而下计算,在返回完成递归过程。
递归算法设计的一般步骤:
- 根据题目设计递归函数中的运算部分;
- 根据题目找到递归公式,题目可能会隐含给出,也可能需要自己进行推导;
- 找到递归出口,即递归的终止条件。
if __name__ == '__main__':
n =int( input())
x=0 # F(n)
y=1 #F(n+1)
ans=0 #F(n+2)
if n==0 :
ans=0
elif n==1:
ans=1
else:
for i in range (n-1):
ans=x+y
x=y
y=ans
print(ans)
递归算法代码:
def f(n):
# 递归出口1
if n == 0:
return 0
# 递归出口2
elif n == 1:
return 1
else:
return f(n - 1) + f(n - 2) # 递归关系式
if __name__ == '__main__':
n = int(input())
ans = f(n)
print(ans)
F = [0]*35
def init():
F[0] = 0
F[1] = 1
for i in range(2, 30):
F[i] = F[i-1]+F[i-2]
if __name__ == '__main__':
m = int(input())
init()
while m > 0:
m -= 1
n = int(input())
print(F[n])
# print(F)
递归算法代码:
F = [0] * 35
def f(n):
# 递归出口1
if n == 0:
F[0] = 0
return 0
# 递归出口2
elif n == 1:
F[1] = 1
return 1
else:
F[n] = f(n - 1) + f(n - 2) # 递归关系式
return F[n]
if __name__ == '__main__':
m = int(input())
f(30)
while m > 0:
m -= 1
n = int(input())
print(F[n])
# print(F)
# 动态规划
row = int(input())
if row == 0:
print(0)
else:
dp = [[0 for i in range(row + 1)] for j in range(row + 1)]
for i in range(row):
line = input().split()
for j in range(i + 1):
dp[i + 1][j + 1] = int(line[j])
for k in range(2, row + 1):
for l in range(1, k + 1):
dp[k][l] = max(dp[k - 1][l - 1],dp[k - 1][l]) + dp[k][l]
last = dp[-1]
print(max(last))
a = [[0] * 101] * 101
if __name__ == '__main__':
n = int(input())
# 输入数字三角形的值
for i in range(1, n+1):
a[i] = input().split()
a[i] = list(map(int, a[i])) # split 分割后都是 字符 这里是转化成数字
#
# for i in range(1, n + 1):
# print(a[i])
# a = list(map(int, a)) # split 分割后都是 字符 这里是转化成数字
# 递推开始
for i in range(n - 1, 0, -1):
# 最后一层逆推
for j in range(0, i):
# 路径选择
if a[i + 1][j] >= a[i + 1][j + 1]:
a[i][j] += a[i + 1][j]
else:
a[i][j] += a[i + 1][j + 1]
# for i in range(1, n + 1):
# print(a[i])
print(a[1][0])
枚举法
python中有自带的排列组合函数。
itertools模块下提供了一些用于生成排列组合的工具函数。
- product(p, q, … [repeat=1]):用序列p、q、…序列中的元素进行排列(元素会重复)。就相当于使用嵌套循环组合。
- permutations(p[, r]):从序列p中取出r个元素的组成全排列,组合得到元组作为新迭代器的元素。
- combinations(p, r):从序列p中取出r个元素组成全组合,元素不允许重复,组合得到元组作为新迭代器的元素。
- combinations_with_replacement(p, r),从序列p中取出r个元素组成全组合,元素允许重复,组合得到元组作为新迭代器的元素。
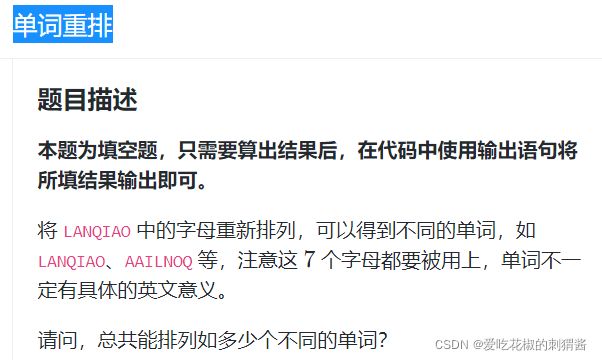
import itertools
if __name__ == '__main__':
s = list("LANQIAO")
print(len(set(itertools.permutations(s))))
枚举算法解题的基本思路:
- 确定枚举解的范围,以及判断条件
- 选取合适枚举方法,进行逐一枚举,此时应注意能否覆盖所有的可能的解
- 在枚举时使用判断条件检验,留下所有符合要求的解。
枚举算法的一般步骤:
- 根据题目确定枚举的范围,并选取合适的枚举方式,不能遗漏任何一个真正解,同时避免重复。
- 为了提高解决问题的效率,看题目是否存在优化,将可能成为解的答案范围尽可能的缩小。
- 根据问题找到合理、准确好描述并且好编码的验证条件。
- 枚举并判断是否符合第三步确定的的条件,并保存符合条件的解。
- 按要求输出枚举过程中留下的符合条件的解。
简单型枚举
简单型枚举就是可以通过简单的 for 循环嵌套就可以解决的问题。
组合型枚举
排列组合相信大家都学习过,组合型枚举就是让你在 n 个中,随机选出 m 个,问你有多少种方案,而且每一种方案选择了哪 m 个,这就是组合型枚举。
组合型枚举有着固定的算法模板.
chosen = []
n = 0
m = 0
def calc(x):
if len(chosen) > m:
return
if len(chosen) + n - x + 1 < m:
return
if x == n + 1:
for i in chosen:
print(i,end=' ')
print('')
return
calc(x + 1)
chosen.append(x)
calc(x + 1)
chosen.pop()
if __name__ == '__main__':
tem = input().split()
n = int(tem[0])
m = int(tem[1])
calc(1)
排列型枚举
排列型枚举相对组合型枚举就简单了一点,就是 n 个的全排列,即从 n 个中选取 n 个但是关心内部的顺序。
排列型枚举也是有着比较成熟的模板。
order = [0] * 20
chosen = [0] * 20
n = 0
def calc(x):
if x == n + 1:
ansTem = ''
for i in range(1, n + 1):
print(order[i],end=' ')
print('')
return
for i in range(1,n+1):
if(chosen[i]==1) :
continue
order[x]=i
chosen[i]=1
calc(x+1)
chosen[i]=0
order[x]=0
if __name__ == '__main__':
n = int(input())
# print(name)
calc(1)
ans = [[] for i in range(10)]
a = ['0']*10
c = input().split()
for i in range(6):
if c[i] == 'A':
a[i] = 1
elif c[i] == 'J':
a[i] = 11
elif c[i] == 'Q':
a[i] = 12
elif c[i] == 'K':
a[i] = 13
else:
a[i] = ord(c[i]) - ord('0')
ans[0].append(a[0])
for i in range(1, 6):
for j in range(len(ans[i - 1])):
ans[i].append(ans[i - 1][j] + a[i])
ans[i].append(ans[i - 1][j] - a[i])
ans[i].append(ans[i - 1][j] * a[i])
ans[i].append(int(ans[i - 1][j] / a[i]))
flag = 0
for j in range(len(ans[5])):
if ans[5][j] == 42:
flag = 1
break
if flag == 1:
print("YES")
else:
print("NO")
# print(c)
# print(a)
# print(ans)
name = []
ans = []
chosen = []
n = 0
m = 0
def calc(x):
if len(chosen) > m:
return
if len(chosen) + n - x + 1 < m:
return
if x == n + 1:
ansTem = ""
for i in chosen:
ansTem = ansTem + name[i - 1] + ' '
# print(ansTem)
ans.append(ansTem)
return
calc(x + 1)
chosen.append(x)
calc(x + 1)
chosen.pop()
if __name__ == '__main__':
tem = input().split()
n = int(tem[0])
m = int(tem[1])
# print(n," ",m)
for i in range(n):
s = input()
name.append(s)
# print(name)
calc(1)
for i in range((len(ans) - 1), -1, -1):
print(ans[i])
Python sorted() 函数
sorted() 函数对所有可迭代的对象进行排序操作。
sort 与 sorted 区别:
-
sort 是应用在 list 上的方法,sorted 可以对所有可迭代的对象进行排序操作。
-
list 的 sort 方法返回的是对已经存在的列表进行操作,无返回值,而内建函数 sorted 方法返回的是一个新的 list,而不是在原来的基础上进行的操作。
import itertools
m, n = map(int, input().split())
s = []
for i in range(m):
s.append(input())
set1 = set(itertools.combinations(s, n)) # 从s中选取n个元素进行组合
for i in sorted(set1):
for j in i:
print(j, end = ' ')
print()
name = []
order = [0] * 20
chosen = [0] * 20
n = 0
def calc(x):
if x == n + 1:
ansTem = ''
for i in range(1, n + 1):
ansTem = ansTem + name[order[i]-1] + ' '
print(ansTem)
return
for i in range(1,n+1):
if(chosen[i]==1) :
continue
order[x]=i
chosen[i]=1
calc(x+1)
chosen[i]=0
order[x]=0
if __name__ == '__main__':
n = int(input())
for i in range(n):
s = input()
name.append(s)
# print(name)
calc(1)
import itertools
m = int(input())
s = []
for i in range(m):
s.append(input())
set1 = itertools.permutations(s)
for i in set1:
for j in i:
print(j, end = ' ')
print()
差分与前缀和
差分法
差分法的应用主要是用于处理区间问题。当某一个数组要在很多不确定的区间,加上相同的一个数。我们如果每个都进行加法操作的话,那么复杂度 O(nm) 是平方阶的,非常消耗时间。
如果我们采用差分法,将数组拆分,构造出一个新的拆分数组,通过对数组区间的端点进行加减操作,最后将数组和并就能完成原来的操作。
这样处理后,时间复杂度降低为 O(N)。
差分法的特点:
-
将对于区间的加减操作转化为对于端点的操作;
-
时间复杂度为 O(n);
-
用于维护区间的增减但不能维护乘除;
-
差分后的序列比原来的数组序列多一个数。
差分算法解题的基本思路: -
b[1]=a[1];
-
从第 2 项到 n 项,利用 b[i]=a[i]-a[i-1]b[i]=a[i]−a[i−1] 差分式;
-
对于区间端点操作加减;
-
差分还原(前缀和)。
-
注意是从1开始,从0开始还有讨论i=0 的情况,使用1的话 b[1]=a[1]-a[0]=a[1]-0;
差分与前缀和是逆操作,常在一起出现,但是先做差分还是先做前缀和就是两种不同的算法,做不做另一种操作也决定了算法不同。
前缀和
前缀和法的应用主要也是用于处理区间问题。
前缀和是指某序列的前 n 项和,可以把它理解为数学上的数列的前 n 项和。当对于某一数组区间进行多次询问,[L,r] 的和时,如果正常处理,那么我们每次都要 [l,r]。查询 N 次,那么时间复杂度也是 O(nm) 也是平方阶的。
如果我们采用前缀和,构造出一个前缀和数组,通过对于端点的值的减法操作就能 O(1) 的求出 [l,r] 的和。然后 N 次查询的,就将复杂度降低为 O(n)
前缀和的特点:
- 将对于区间的求和操作转化为对于端点值的减法的操作;
- 区间求和操作的时间复杂度为 O(1);
- 数组存放时要从 1 开始;
- 前缀和数组比原来的数组序列多一个数,第 0 个
前缀和算法解题的基本思路:
- 利用 sum[i]=a[i]+sum[i-1]sum[i]=a[i]+sum[i−1] 差分式;
- 从第 1 项到 n 项,且第 0 项无数据默认为 0;
- 对于区间求和的操作转化为端点值相减。
b = [0] * 100005 # M的范围为100000
n, m = map(int, input().split())
while m:
m -= 1
l, r, v = map(int, input().split()) # 起始点,终止点,花费
b[l+1] += v
b[r + 1+1] -= v
for i in range(1, n+1):
b[i] = b[i - 1] + b[i]
sum = 0
for i in range(1,n+1):
sum += b[i]
print(sum)
# 前缀和
sum1 = [0] * 100005
n, m = map(int, input().split())
a = list(map(int, input().split()))
# split 分割后都是 字符 这里是转化成数字
#print(a)
for i in range(1, n + 1):
sum1[i] = sum1[i - 1]
sum1[i] += a[i - 1] # 分割完后,a[]是从0开始,所以要减1
while m > 0:
m -= 1
l, r = map(int, input().split())
print(sum1[r] - sum1[l - 1])
二分查找算法
折半查找的基本思想:
在有序表中(low,high,low<=high),取中间记录即 [(high+low)/2] 作为比较对象。
- 若给定值与中间记录的关键码相等,则查找成功
- 若给定值小于中间记录的关键码,则在中间记录的左半区继续查找
- 若给定值大于中间记录的关键码,则在中间记录的右半区继续查找
不断重复上述过程,直到查找成功,或所查找的区域无记录,查找失败。
二分查找的特征:
- 答案具有单调性;
- 二分答案的问题往往有固定的问法,比如:令最大值最小(最小值最大),求满足条件的最大(小)值等。
#在单调递增序列a中查找>=x的数中最小的一个(即x或x的后继)
while low<high:
mid=(low+high)/2
if(a[mid]>=x):
high=mid
else:
low=mid+1
#在单调递增序列a中查找<=x的数中最大的一个(即x或x的前驱)
while low<high:
mid=(low+high+1)/2
if(a[mid]<=x):
low=mid
else:
high = mid-1
N, K = map(int, input().split())
MAX = 0
cakes = []
for _ in range(N):
w, h = map(int, input().split())
MAX = max(MAX, w, h)
cakes.append([w, h])
def cal(size):
cnt = 0
for w, h in cakes:
cnt += (h // size) * (w // size)
return cnt
l, r = 0, MAX
while l < r:
mid = l + r + 1 >> 1
if cal(mid) >= K: l = mid
else: r = mid - 1
print(l)
# m次方根
# 直接用python自带的math
import math
n, m = map(int, input().split())
ans = math.pow(n, 1/m) # n的根号m次方
print('{:.7f}'.format(ans))

补充材料
Python pow() 函数
描述
pow() 方法返回 xy(x 的 y 次方) 的值。
语法
以下是 math 模块 pow() 方法的语法:
import math
math.pow( x, y )
内置的 pow() 方法
pow(x, y[, z])
# 函数是计算 x 的 y 次方,如果 z 在存在,则再对结果进行取模,其结果等效于 pow(x,y) %z。
注意:pow() 通过内置的方法直接调用,内置方法会把参数作为整型,而 math 模块则会把参数转换为 float。
参数
x – 数值表达式。
y – 数值表达式。
z – 数值表达式。
返回值
返回 x y x^y xy(x的y次方) 的值。
import math # 导入 math 模块
print "math.pow(100, 2) : ", math.pow(100, 2)
# 使用内置,查看输出结果区别
print "pow(100, 2) : ", pow(100, 2)
print "math.pow(100, -2) : ", math.pow(100, -2)
print "math.pow(2, 4) : ", math.pow(2, 4)
print "math.pow(3, 0) : ", math.pow(3, 0)
以上实例运行后输出结果为:
math.pow(100, 2) : 10000.0
pow(100, 2) : 10000
math.pow(100, -2) : 0.0001
math.pow(2, 4) : 16.0
math.pow(3, 0) : 1.0
n = 0.0
m = 0
l = 0.0
r = 0.0
mid = 0.0
eps = 0.00000001
def pd(a, m):
c = 1.0
cnt = int(m)
while cnt > 0:
c = c * a
cnt -= 1
if c >= n:
return True
else:
return False
if __name__ == '__main__':
n, m = input().split()
l = 0
r=n=int(n)
while l + eps < r:
mid = (l + r) / 2
if (pd(mid, m)):
r = mid
else:
l = mid
print("%.7f" % l)
贪心算法
贪心算法有一个必须要注意的事情。贪心算法对于问题的要求是,当前的选择,不能影响后续选择对于结果的影响。
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
所谓的贪心选择性质就是,该问题的每一步选择都在选择最优的情况下能够导致最终问题的答案也是最优。
或者说是无后效性,如果该问题的每一步选择都对后续的选择没有影响,就可以是应用贪心算法。
贪心算法的设计步骤
- 证明原问题的最优解之一可以由贪心选择得到。
- 将最优化问题转化为这样一个问题,即先做出选择,再解决剩下的一个子问题。
- 对每一子问题一一求解,得到子问题的局部最优解;
- 把子问题的解局部最优解合成原来解问题的一个解
t = [100, 50, 20, 5, 1]
# 钱的面值
def change(t, n):
# m是张数
m = [0 for _ in range(len(t))]
# print(m) #[0, 0, 0, 0]
for i, money in enumerate(t):
# print(i) #0 1 2 3
# print(money)
# i是当前的编号 举个例子 n是376 money是100
m[i] = n // money # 商3
# n还剩多少取余
n = n % money # 取余76 76不够100的
# print(m)
# print(n)
return m
if __name__ == '__main__':
N = int(input())
m = change(t,N)
for i in range(len(m)):
print('{}:{}'.format(t[i], m[i]))
# 搬运次数
N = 0
# 起点与终点
From = 0
To = 0
# 最大搬运次数
maxAns = 0
T = 0
if __name__ == '__main__':
T = int(input())
while (T > 0):
T -= 1
move = [0] * 205
N = int(input())
for i in range(N):
From, To = input().split()
From = int(From)
To = int(To)
From = int((From - 1) / 2)
To = int((To - 1) / 2)
if From > To:
temp = From
From = To
To = temp
for j in range(From, To + 1):
move[j] += 1
maxAns = max(move[j], maxAns)
if maxAns % 2 == 1:
maxAns = (maxAns >> 1) + 1
else:
maxAns =(maxAns >> 1)
print(maxAns*10)
class Food:
def __init__(self, w, v, aver):
self.w = w
self.v = v
self.aver = aver
def __repr__(self):
# print(11)
return repr((self.w, self.v, self.aver))
# def cmp(foodA: Food, foodB: Food):
# if foodA.aver >= foodB.aver:
# return True
#
# else:
# return False
#
#
# 当然 python 的 sort 是不需要写 cmp 函数的,这里我们使用 sorted 就不用 cmp 函数了
if __name__ == '__main__':
foods = []
C = 0.0
Value = 0.0
n, C = map(int, input().split())
for i in range(n):
food = Food(0, 0, 0)
food.v, food.w = map(int, input().split())
food.aver = food.v / food.w
foods.append(food)
# print(food.aver)
# print(foods)
# 性价比排序
foods.sort(key=lambda f: f.aver, reverse=True)
# for i in range(n):
# print(foods[i].aver)
sum=0
for i in range(n):
sum+= foods[i].w
# 当背包(肚子)能装下所有物品(菜)时,直接输出所有的物品(菜品)价值之和
if sum<=C :
for i in range(n):
Value+=foods[i].v;
print(Value)
# 当背包(肚子)不能装下所有物品时应该由性价比的顺序,选择装入的物品
else:
for i in range(n):
if foods[i].w<=C:
Value=Value+foods[i].v
C=C-foods[i].w
# 直接将剩余的C加入即可
else:
Value+=C*foods[i].aver
C=0
if C==0:
break
print("%.3f" % Value)
蓝桥杯真题精讲一
class Stu:
def __init__(self, inD, answQ, outD):
self.inD = inD
self.answQ = answQ
self.outD = outD
self.sum1 = inD + answQ + outD
self.sum2 = inD + answQ
if __name__ == '__main__':
stu = []
C = 0.0
Value = 0.0
n = int(input())
for i in range(n):
a, b, c = map(int, input().split())
ss = Stu(a, b, c)
stu.append(ss)
# print(food.sum1)
# print(foods)
# 贪心过程及结果计算
# 关于排序:
# 如果先按a准则,a相同再按b准则,b相同再按c准则排序
# 那么可以按c排序,再按照b排序,再按照a排序即可
# 如下所示:
stu.sort(key=lambda f: f.sum2, reverse=False)
stu.sort(key=lambda f: f.sum1, reverse=False)
# 当然也可以按顺序给值:
# stu.sort(key=lambda f: (f.sum1, f.sum2), reverse=False)
# for i in range(n):
# print(foods[i].aver)
res = 0
t = 0
for i in range(n):
t += stu[i].sum2
res += t
t += stu[i].outD
print(res)
a = [1, 3]
n = 50
def init():
for i in range(n):
a.append(a[i] + a[i + 1])
def comp():
for i in range(n):
b = a[i] / a[i + 1]
if abs(b - 0.618034) <= 0.000001:
s = str(a[i]) + '/' +str( a[i + 1])
return s
# 相比C++ ,Python 对于字符串的处理就简单了很多
if __name__ == '__main__':
init()
ans = comp()
print(ans)
def comp(n: int):
day = 1 # 第几天
gz = 0 # 工资
sum: int = 0 # 总工资
while day <= n:
gz += 1
for i in range(gz):
sum += gz
day += 1
if day > n:
return sum
if __name__ == '__main__':
n = int(input())
ans = comp(n)
print(ans)
import os
import sys
if __name__ == '__main__':
n = int(input())
str = input().split()
# print(str)
a = list(map(int , str))
# print(a)
profit = -0x3f3f3f3f
for i in range(n - 1):
for j in range(i + 1, n):
if a[j] - a[i] > profit:
profit = a[j] - a[i]
print(profit)
蓝桥杯真题精讲二
# 第一种解法 简单多次排序
import queue
q = queue.PriorityQueue()
if __name__ == '__main__':
n = int(input())
num = list(map(int, input().split()))
cnt = 0
while(len(num)>1):
num.sort()
x=num[0]
y=num[1]
cnt+=(x+y)
del num[0]
del num[0]
num.append(x+y)
print(cnt)
# 第二种解法 优先队列
import queue
q = queue.PriorityQueue()
if __name__ == '__main__':
n = int(input())
num = list(map(int, input().split()))
for _ in num:
q.put([_])
cnt = 0
if q.qsize() == 1:
print(q.get())
else:
while q.qsize() > 1:
x = q.get()[0]
y = q.get()[0]
cnt += (x + y)
q.put([x + y])
print(cnt)
import queue
if __name__ == '__main__':
M, N, K, L, D = map(int, input().split())
x = [0] * 10055
y = [0] * 10055
c = [0] * 10055
o = [0] * 10055
while D > 0:
D -= 1
xi, yi, pi, qi = map(int, input().split())
if xi == pi:
y[min(yi, qi)] += 1
else:
x[min(xi, pi)] += 1
for i in range(1, K + 1):
maxn = -1
p = 0
for j in range(1, M):
if x[j] > maxn:
maxn = x[j]
p = j
x[p] = 0
c[p] += 1
for i in range(1, L + 1):
maxn = -1
p = 0
for j in range(1, N):
if y[j] > maxn:
maxn = y[j]
p = j
y[p] = 0
o[p] += 1
for i in range(10050):
if c[i] != 0:
print(i, end=' ')
print('')
for i in range(10050):
if o[i] != 0:
print(i, end=' ')