第十二届蓝桥杯大赛软件赛省赛 C/C++ 大学B组

试题A ：空间

67108864

试题B ：卡片

// 答案是 3181
#include 
using namespace std;

int nums[15];

bool check(int x)
{
    while (x)
    {
        int now = x % 10;
        x /= 10;
        if (nums[now] < 1) return false;
        nums[now] -- ;
    }
    return true;
}

int main()
{
    for (int i = 0; i <= 9; i ++ ) nums[i] = 2021;
    
    for (int i = 1; ; i ++ )
    {
        if (!check(i))
        {
            cout << i - 1;
            return 0;
        }
    }
}

试题C ：直线

• 需要注意当垂直于x轴使无法计算斜率
• 注意计算b时，式子中不要涉及到k，可以用整型，就不要用浮点数计算

// 答案是40257
#include 
#include 
using namespace std;

const int N = 30 * 30;

struct Point
{
    int x, y;
}p[N];
int cnt;

map<pair<double, double>, int> ma;

int main()
{
    for (int i = 0; i < 20; i ++ )
        for (int j = 0; j < 21; j ++ )
        {
            p[cnt].x = i; p[cnt].y = j; cnt ++ ;
        }
    
    int res = 20 + 21;
    
    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < cnt; j ++ )
        {
            int x1 = p[i].x, y1 = p[i].y, x2 = p[j].x, y2 = p[j].y;
            if (x1 == x2 || y1 == y2) continue;
            double k = 1.0 * (y2 - y1) / (x2 - x1);
            double m = 1.0 * (x2 * y1 - x1 * y2) / (x2 - x1);
            if (ma[{k, m}] == 0)
            {
                res ++ ;
                ma[{k, m}] = 1;
            }
        }
    cout << res;
}

试题D ： 货物摆放

• $a\ast b\ast c==n$，不可能直接枚举，发现abc的特点就是它们都是n的约束，因此我们可以直接枚举n的所有约数，复杂度大大降低

// 答案是2430
#include 
#include 
using namespace std;

typedef long long ll;

const ll n = 2021041820210418;

int main()
{
    ll res = 0;
    
    vector<ll> ve;
    
    for (ll i = 1; i * i <= n; i ++ )
    {
        if (n % i == 0)
        {
            ve.push_back(i);
            if (i * i != n) ve.push_back(n / i);
        }
    }
    
    for (auto i : ve)
        for (auto j : ve)
            for (auto k : ve)
                if (i * j * k == n)
                    res ++ ;
    cout << res;
}

试题E ：路径

// 答案是10266837
#include 
#include 
using namespace std;

const int N = 2030;

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

int dist[N][N];

int main()
{
    memset(dist, 0x3f, sizeof dist);
    
    for (int i = 1; i <= 2021; i ++ )
        for (int j = 1; j <= 2021; j ++ )
        {
            if (i == j) dist[i][j] = 0;
            else if (abs(i - j) <= 21) dist[i][j] = min(dist[i][j], i * j / gcd(i, j));
        }
    
    for (int i = 1; i <= 2021; i ++ )
        for (int j = 1; j <= 2021; j ++ )
            for (int k = 1; k <= 2021; k ++ )
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
    
    cout << dist[1][2021];
}

试题F ：时间显示

#include 
#include 
using namespace std;

typedef long long ll;

int main()
{
    ll n; cin >> n;
    ll time = n / 1000;
    ll ss = time % 60;
    ll mm = time / 60 % 60;
    ll hh = time / 3600 % 24;
    printf("%02lld:%02lld:%02lld", hh, mm, ss);
}

试题G ：砝码称重

• 砝码可以放在天平两边或者不放，相当于砝码的重量可以为正贡献也可以为负贡献或者没有贡献
• 由于j + w[i]，因此可能会出现越界，要把M开大一些

#include 
#include 
using namespace std;

const int N = 110, M = 2e5 + 10;

int n, w[N];
bool f[N][M];

int main()
{
    cin >> n;
    int sum = 0;
    for (int i = 1; i <= n && cin >> w[i]; i ++ ) sum += w[i];
    
    f[0][0] = true;
    
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 0; j <= 100000; j ++ )
        {
            f[i][j] = f[i - 1][j];
            f[i][j] |= f[i - 1][abs(j - w[i])];
            f[i][j] |= f[i - 1][j + w[i]];
        }
    }
    
    int res = 0;
    for (int i = 1; i < M; i ++ )
        if (f[n][i])
            res ++ ;
    cout << res;
}

// TLE
#include 
using namespace std;

const int N = 110, M = 1e5 + 10;

int n, w[N];
bool vis[M];

void dfs(int i, int sum)
{
    if (i == n + 1)
    {
        vis[abs(sum)] = true;
        return ;
    }
    
    dfs(i + 1, sum);
    dfs(i + 1, sum - w[i]);
    dfs(i + 1, sum + w[i]);
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n && cin >> w[i]; i ++ );
    
    dfs(1, 0);
    
    int res = 0;
    for (int i = 1; i < M; i ++ )
        if (vis[i])
            res ++ ;
    cout << res;
}

试题H ：杨辉三角形

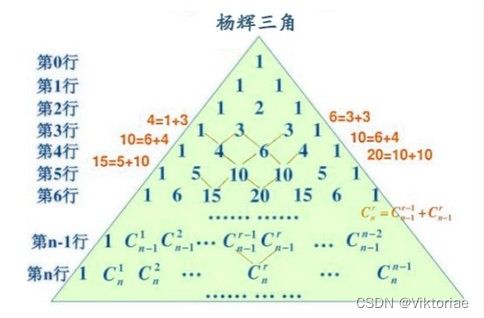
• 由于左右对称，要找第一次出现的位置，因此右半部分不需要考虑
• 杨辉三角中每个数都可以用 组合 来表示，且同一行中的下角标相同，同一斜行的上角标相同
• 1e9数据，以行和列来枚举是不现实的，因此我们考虑以每一斜行（下面以“列”代称）来入手
• 每一列中，从上到下严格单调递增，因此，在每一列中，可以用二分查找n，而且我们发现在仅使用一半的杨辉三角以后，每一列中最上面的那个数是$C_{2i}^i$，而最下面的那个数仅与当前枚举的行数有关，最多肯定是n行，则为$C_{2n}^1$；列与列之间，最上面的数是递增的，且越靠下的列出现第一次出现的数的概率更高，因此，我们从最下面的列开始枚举，从计算最上面的数可知我们只需要枚举到第十七列（从第零列开始）
• 关于如果计算$C_n^m$的优化

#include 
using namespace std;

typedef long long ll;

int x;

ll C(int n, int m)
{
    ll res = 1;
    for (int i = n, j = 1; i >= n - m + 1; i -- , j ++ )
    {
        res = res * i / j;
        if (res > x) return res;
    }
    return res;
}

bool check(int k)
{
    int l = 2 * k - 1, r = max(l, x) + 1;   // 保证右边界大于等于左边jie
//    int l = 2 * k, r = x;
    while (l + 1 != r)
    {
        int mid = l + r >> 1;
        if (C(mid, k) >= x) r = mid;
        else l = mid;
    }
    
    if (C(r, k) == x)
    {
        cout << 1ll * r * (r + 1) / 2 + k  + 1;
        return true;
    }
    return false;
}

int main()
{
    cin >> x;
    
    for (int i = 17; ; i -- )
        if (check(i))
            break;
}

// 20%分数
#include 
#include 
using namespace std;

int f[2510][2510];
int cnt;

int main()
{
    int n; cin >> n;
    
    f[0][0] = 1;
    for (int i = 1; i <= 2500; i ++ )
    {
        for (int j = 1; j <= i; j ++ )
        {
            f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
            cnt ++ ;
            if (f[i][j] == n)
            {
                cout << cnt;
                return 0;
            }
        }
    }
}

试题I ：双向排序（暂跳）

试题J ：括号序列