八大排序之归并排序
归并排序引论:
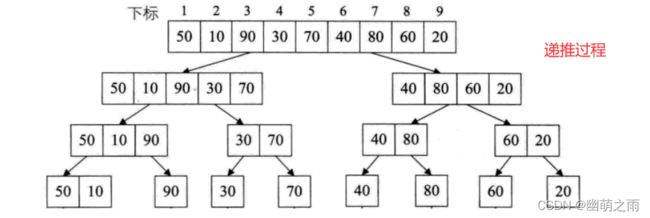
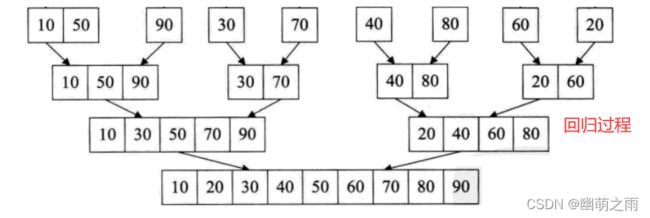
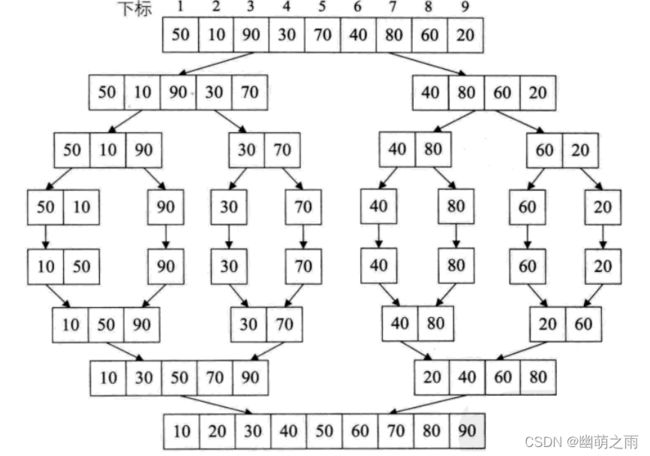
归并排序就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录,则可以看成是有n个有序的子序列,没个子序列的长度为1,然后两两归并,得到[n/2]([x]表示不小于x的最小整数)个长度为2或1的有序子序列;然后两两归并,....,如此重复,直至得到一个长度为n的有序序列为止,这种方法称为2路归并排序。
一般我们最先想到的是采用递归的方法解决,那么我们需要直到递推和回归,递推的是划分之后的乱序数列,回归的是有序的数列,递推的过程可以看做一棵正的二叉树,回归的过程可以看做一棵倒着的二叉树。
那么全过程就是这样滴:
在具体实现时,我们通常重新开辟一块空间,在这块空间里存放已经有序的子序列。所以在实现时,我们先将原序列划分,划分完毕之后,在回归的过程中进行排序,将排序好的数据先放在新空间中,之后再将新空间中的数据转移到原空间中,因为新空间我们最终是要释放的,这里只是利用一下。
代码实现:
void Merge(int* src, int *dest, int left, int m, int right)
{
int i = left, j = m + 1;
int k = left;
while (i <= m && j <=right)
{
dest[k++] = src[i] <= src[j] ? src[i++] : src[j++];
}
while (i <= m)
{
dest[k++] = src[i++];
}
while (j <=right)
{
dest[k++] = src[j++];
}
}
void Copy(int* src, int* dest, int left, int right)
{
while (left <= right)
{
dest[left] = src[left];
++left;
}
}
void MergePass(int* src, int* dest, int left, int right)
{
if (left < right)
{
int mid = (right + left) / 2;
MergePass(src, dest, left, mid);
MergePass(src, dest, mid + 1, right);
Merge(src, dest, left, mid, right);
Copy(dest, src, left, right);
}
}
void MergeSort(int* br, int n)
{
if (br == NULL || n < 2)return;
int* tmp = new int[n];
MergePass(br, tmp, 0, n - 1);
delete[]tmp;
}
除了使用递归的方法解决,我们能不能用非递归的方法解决呢?当然是可以的
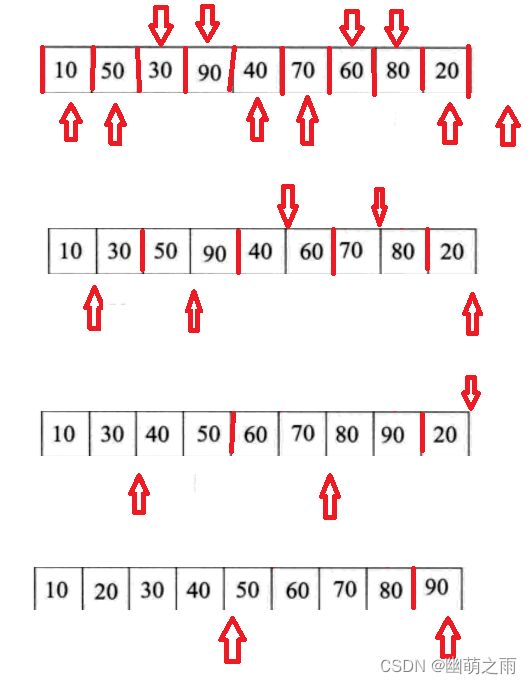
我们可以先选取两个数据元素个数都为1的子序列进行排序,然后再去两个数据元素为2的子序列进行排序,之后是4,8...2^n,以此类推,直到全部数列有序,那么如何实现呢?我们只需要定义四个指针,分别用来指向第一个子序列的左边界,右边界,右序列的左边界,右边界,逐一比较排序即可。
图解:
代码实现:
//时间复杂度O(nlogn) 空间复杂度O(nlogn) 稳定性:稳定
void Merge(int* ar, int len,int gap)
{
int low1, high1, low2, high2;
//申请四个指针,分别用来标识两个组的左右端
low1 = 0;
high1 = low1 + gap - 1;
low2 = high1 + 1;
high2 = low2 + gap - 1