强化学习可以用来调参?人工智能炼丹师《Using Deep Q-Learning to Control Optimization Hyperparameters》论文解读
文献链接:[1602.04062v1] Using Deep Q-Learning to Control Optimization Hyperparameters (arxiv.org)
在探索强化学习应用的无目的搜索中,偶然发现一篇让我让很是感兴趣的文章:利用强化学习去进行超参数的调节。
超参数指的是人工设定的,在训练过程中不会改变的一系列参数类似学习率,步长,卷积层,卷积核等等,且一般为了达到比较良好的效果,炼丹师们会不断地改变这些超参数,然后训练,试图进一步获得更好的训练结果。但是在一般情况下,需要进行一次完整的训练之后才能去调整,而调整一般也是比较寻玄学的。
一部分、是没有目的地试(比如深度学习具有黑箱的效应,可解释性很差),经典的方法有网格搜索,随即搜索。他们的缺点是资源耗费巨大,范围广但是无法保证结果。
另外就是比较先进的算法,例如粒子群优化,遗传算法和主流的贝叶斯优化算法。他们能在部分的超参数调节中发挥的较好,可以得到相对传统方法更优的超参数序列。
作者认为,可以利用强化学习的方法来根据当前参数以及其他训练过程中产生的数据进行一个最优的参数调整决策,可行性有以下几点支撑:
- 强化学习可以很好地解决时间序贯问题,参数的调整过程符合要求
- 参数的调整具有很好的马尔科夫特性,可以很好地利用MDP进行建模
作者以学习率这为例,引出一种基于DQN的,可跟随训练自行调节的梯度下降算法:Q-gd,分为两种环境,搜索方法不同。第一种环境的搜索方法按照Armijo line search procedure,迭代后将参数降低一个确定值或者重置为初始值;第二种环境的搜索方法改进了第一种,迭代后可以增加或减少,但是不能重置。
接下来我就不按照原文的顺序介绍强化学习,直接进行动作,状态,奖励的建模的建模。
1.动作的定义
在进行单一参数(学习率)的调整时,Q—GD有两类:
Q-GD1就是减少某一常数和重置两个动作
Q-GD2有减少某一常数和增加某一常数两个动作
原文中的算法图
初始化输入:初始值(需要进行梯度下降的值),初始学习率,学习好的DQN,最大迭代次数
- 将输入的值(迭代数据,初始步长)设为初始值,根据代价函数计算梯度
- 当迭代次数小于最大迭代次数时:
- 计算当前的状态(下一部分会讲)
- 根据DQN选择动作(减半,加倍或者接受)
- 如果动作是减半则学习率减半
- 如果动作是加倍则学习率加倍
- 如果动作是接受则输出需要的学习率(根据1,2两类分别考虑)
- 进行梯度下降
直到迭代到最大迭代次数T,则输出最终结果
2.环境与状态的定义
在对环境进行定义时,既要满足当前状态包含历史信息,又要满足马尔可夫特性。随人可以利用初始信息和之前所有的迭代信息进行定义,但是对于具有大量变量的目标函数,这种方法在计算上是令人望而却步的,并且会严重限制训练的DQN推广到更广泛的函数族的能力,普适性差。所以我们试图从过去提炼出一个有用的特征作为状态。
作者以nonmontone line search(非单调线搜索)为启发,因为它提供了一个有效的标准来确定与函数变量大小或类型无关的学习率。
非单调线搜索选择学习率,使得新迭代充分小于过去M 次迭代的最大值,![]() 则其中前M次迭代的最大值可以经过编码后作为状态的表征之一。作者使用一种编码来表示:当前迭代的值和过去M次迭代最大值之间的大小关系:
则其中前M次迭代的最大值可以经过编码后作为状态的表征之一。作者使用一种编码来表示:当前迭代的值和过去M次迭代最大值之间的大小关系: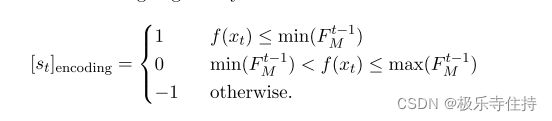
作者又受RPROP启发设计对其度量(measure of alignment,我也没懂这是什么意思)
 按照公式来说,可能是在这个时刻是否出现转折,具体还需参考RPROP的方法(有点懒没去找)
按照公式来说,可能是在这个时刻是否出现转折,具体还需参考RPROP的方法(有点懒没去找)
在定义了这下特殊的状态表征之后,状态可以表示为六个量,分别是
- 当前的学习率
- 当前的
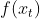
- 搜索方向和梯度的点积
- 与前M次最小/大值的比较编码
![s_t[encoding]]](http://img.e-com-net.com/image/info8/12a004d0d44b43c5bb1cf118ce385958.gif)
- 迭代的次数
- 对齐度量
![s_t[alignment]]](http://img.e-com-net.com/image/info8/97d42b58564c419b8223ec1c217b45a0.gif)
额外的,再将这六个量归一化,使其能够普适![]() ,这里的max和min是指每一个表征的规定的最大/小值。这样操作可以使所有值的范围在[-1,1]中
,这里的max和min是指每一个表征的规定的最大/小值。这样操作可以使所有值的范围在[-1,1]中
3.奖励的定义
奖励部分,作者尝试了三种奖励的设计,分别是与![]() 下限的反向距离
下限的反向距离
作者分别测试了三种奖励函数的效果如下图,具有最高的Rmax值时集中于最低的![]()
4.训练一个DQN网络
利用了经验回访技巧,增强对于交互信息的利用。一些关于细节的设定可以关注原文,不赘述
5.训练结果
结果证明,Q_GD算法在泛化性能,结果上均优于其他的算法,且Q_GDv1算法性能最好。
6.意义
本篇文章是第一篇尝试使用RL来进行HPO的实验,结果很是不错,奠定了相关领域未来的发展基础。接下来我也会更新这一方向的论文。



