实验一 序列的傅里叶变换和离散傅里叶变换及其关系

一、简述实验目的及实验原理；

实验目的：

1）掌握序列傅里叶变换DTFT的计算机实现方法；

2）掌握序列DFT基本理论及其计算机实现方法；

3）掌握序列傅里叶变换DTFT和序列DFT的关系；

4）理解 中 值与 的实际角频率 之间的对应关系。

实验内容实现：

1.DTFT：

function [Xk]=dft(xn, N)

l=length(xn);

if l

2.DFT：

function [Xk]=dft(xn, N)

l=length(xn);

if l

3.

clc,clear,close all

xn=[1,1,1,1];

M=1000;

k=0:1:M-1;

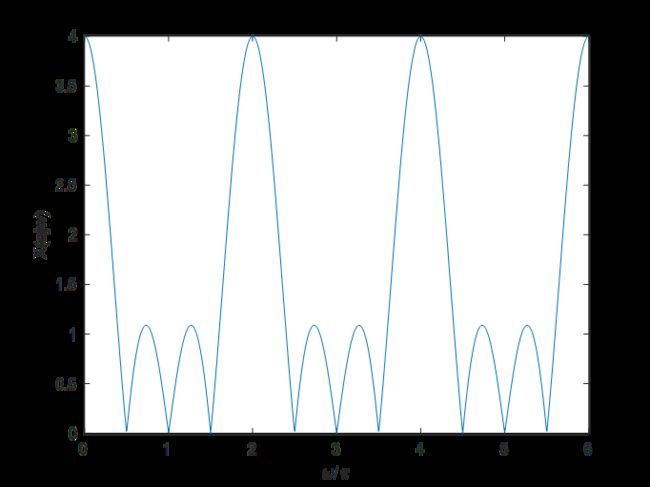
w=6*pi/M*k;

Xejw=dtft(xn,w);

% subplot(511);

plot(w/pi,abs(Xejw));

ylabel('X(ejw)');

xlabel('\omega/\pi');

 

4.1

clc,clear,close all

xn=[1,1,1,1];

M=1000;

k=0:1:M-1;

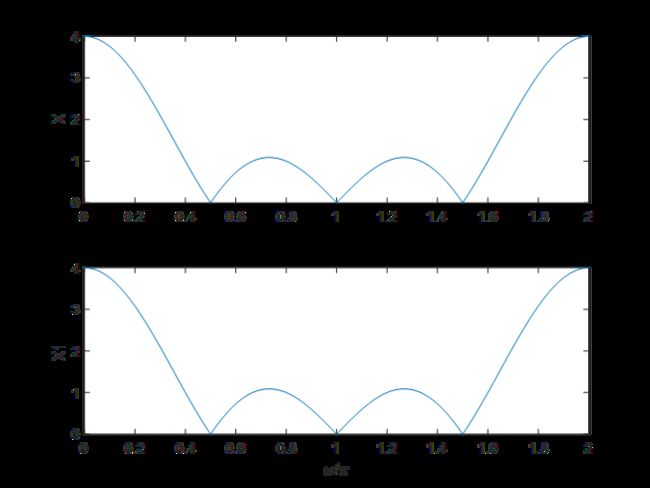
x1=[xn,zeros(1,28)];

w1=2*pi/1000*k;

X=dtft(xn,w1);

subplot(211);

plot(w1/pi,abs(X));

ylabel('X');

subplot(212);

X1=dtft(x1,w1);

plot(w1/pi,abs(X1));

ylabel('X1');

xlabel('\omega/\pi');

 

4.2

clc,clear,close all

xn=[1,1,1,1];

M=4;

k=0:1:M-1;

Xk1=dft(xn,M);

subplot(211);

stem(2/M*k,abs(Xk1));

ylabel('Xk1');



M=32;

k=0:1:M-1;

Xk2=dft(xn,M);

subplot(212);

stem(2/M*k,abs(Xk2));

xlabel('\omega/\pi');

ylabel('Xk2');

 

• 实验结论

结论一：在时域有限长的情况下，频域中是无限的；而在时域是离散的情况下，频域会产生周期延拓。

结论二：是相同的，是否补零对序列的DTFT无影响。

结论三：补零可以减小栅栏效应但不能提高频率的分辨率，因为频率分辨率是与其有效长度有关，在补零后虽然采样点多了，但是有效长度却没有变，所以频率分辨率不变。

• 思考题。

实际角频率ωk=（2π/N）k ,k=0,1,2…N-1