2022蓝桥杯C++B组省赛题目及个人解法

个人已知的错误已经修改 多是实验室同学讨论整理得出 如有错误恳请指正 有问题也欢迎在评论区提问 看到都会回复

代码写的有点丑 轻喷

A 九进制转十进制

#include 
using namespace std;

#define ll long long
#define db double

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

int main() {
    ll a = 2022, b = 1;
    ll ans = 0;
    while (a) {
        ans += a % 10 * b;
        a /= 10;
        b *= 9;
    }
    cout << ans;
    return 0;
}
// 1478

B 顺子日期

这题题面有争议 012到底算不算顺子，算则14，不算则是4

#include 
using namespace std;

#define ll long long
#define db double

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

string _to_string(int n) {
    string str = "";
    while (n) {
        str += (char)(n % 10 + '0');
        n /= 10;
    }
    reverse(str.begin(), str.end());
    return str;
}

int md[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int n = 2022, y = 1, r = 1, ans = 0;
int main() {
    while (1) {
        int num = n * 10000;
        num += y * 100;
        num += r;
        string s = _to_string(num);
        cout << s << '\n';
        int flag = 0;
        for (int i = 0; i < s.size(); i++) {
            if (i >= 2) {
                for (int j = i - 1; j <= i; j++) {
                    if (s[j] != (char)(s[j - 1] + 1)) break;
                    if (j == i) flag = 1;
                }
            }
        }
        if (flag) {
            cout << "1\n";
            ans++;
        }
        if (r == md[y]) {
            ++y;
            r = 1;
        } else
            ++r;
        if (y == 13) break;
    }
    cout << ans;
    return 0;
}
// 14

C 刷题统计

天数能达到$10^{18}$，要用long long

复杂度$O(1)$

#include 
using namespace std;

#define ll long long
#define db double

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

int main() {
    ll n, a, b, num = 0;
    cin >> a >> b >> n;
    ll wt = a * 5 + b * 2;
    ll d = n / wt * 7;
    n %= wt;
    if (n == 0) {
        cout << d;
        return 0;
    }
    for (ll i = 0;; i++) {
        ll t = i % 7;
        if (t == 6 || t == 5) {
            n -= b;
        } else
            n -= a;
        if (n <= 0) {
            cout << d + i + 1;
            return 0;
        }
    }
    return 0;
}

D 修剪灌木

第n+2个来回过程中灌木的状态和第2个来回时的状态都相同，所以我们只要模拟两个来回，维护最大值即可

复杂度$O(n)$

#include 
using namespace std;

#define ll long long
#define db double

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

ll n, t = 1;
ll a[10005], maxt[10005];

int main() {
    scanf("%lld", &n);
    for (int i = 0; i < n; i++, t++) {
        maxt[i] = max(maxt[i], t + a[i]);
        a[i] = -t;
    }
    for (int i = n - 2; i >= 0; i--, t++) {
        maxt[i] = max(maxt[i], t + a[i]);
        a[i] = -t;
    }
    for (int i = 1; i < n; i++, t++) {
        maxt[i] = max(maxt[i], t + a[i]);
        a[i] = -t;
    }
    for (int i = n - 2; i >= 0; i--, t++) {
        maxt[i] = max(maxt[i], t + a[i]);
        a[i] = -t;
    }
    for (int i = 0; i < n; i++) {
        printf("%lld\n", maxt[i]);
    }
    return 0;
}

E X进制减法

每一位贪心可取最小位权即为最佳答案

#include 
using namespace std;

#define ll long long
#define db double
#define maxn 100005

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

ll ans = 1000000008, top, n, ma, mb, a[maxn], b[maxn], bit[maxn], l[maxn];

int main() {
    scanf("%lld", &n);
    scanf("%lld", &ma);
    for (int i = 0; i < ma; i++) {
        scanf("%lld", &a[ma - i]);
        l[ma - i] = max(l[ma - i], a[ma - i] + 1);
    }
    scanf("%lld", &mb);
    for (int i = 0; i < mb; i++) {
        scanf("%lld", &b[mb - i]);
        l[mb - i] = max(l[mb - i], b[mb - i] + 1);
    }
    bit[ma] = n;
    bit[mb] = n;
    bit[1] = 2;
    top = max(ma, mb);
    for (int i = 1; i <= top; i++) {
        if (bit[i]) continue;
        bit[i] = l[i];
    }
    ll aval = 0, bval = 0, c = 1;
    for (int i = 1; i <= top; i++) {
        aval += a[i] * c;
        bval += b[i] * c;
        c *= bit[i];
    }
    printf("%lld", aval - bval);
    return 0;
}

F 统计子矩阵

暂时只会$O(n^4)$的二维前缀和方法，能过70%的数据，求指教AC的方法

#include 
using namespace std;

#define ll long long
#define db double

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

int a[505][505];
int n, m, k, ans;
int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            a[i][j] += a[i][j - 1];
        }
    }
    for (int j = 1; j <= m; j++) {
        for (int i = 1; i <= n; i++) {
            a[i][j] += a[i - 1][j];
        }
    }
    // for(int i=1;i<=n;i++){
    //	for(int j=1;j<=m;j++){
    //		printf("%d ",a[i][j]);
    //	}
    //	printf("\n");
    // }
    for (int i1 = 1; i1 <= n; i1++) {
        for (int j1 = 1; j1 <= m; j1++) {
            for (int i2 = i1; i2 <= n; i2++) {
                for (int j2 = j1; j2 <= m; j2++) {
                    int tmp = a[i2][j2] - a[i2][j1 - 1] - a[i1 - 1][j2] +
                              a[i1 - 1][j1 - 1];
                    // printf("%d %d %d %d : %d\n",i1,j1,i2,j2,tmp);
                    if (tmp <= k) ++ans;
                }
            }
        }
    }
    printf("%d", ans);
    return 0;
}

G 积木画

考点：动态规划

该题有原题：洛谷【覆盖墙壁】

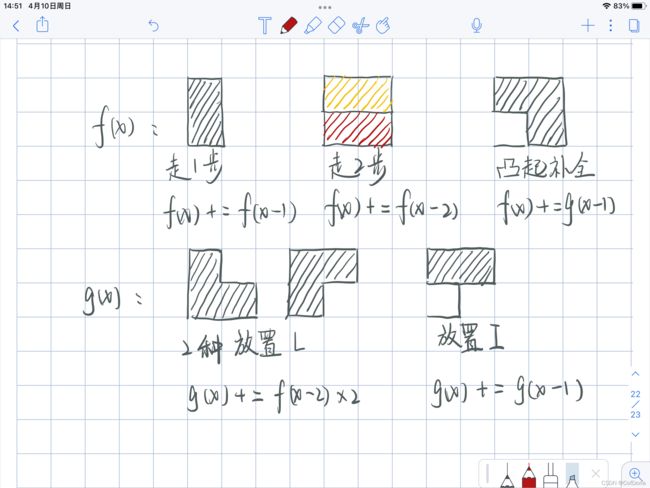
设$f_i$为第 $i$ 位结束且无凸起的方案数，$g_i$为第 $i$ 位结束且有凸起的方案数

状态转移见图和代码。

可以开两个长度为1e7的数组，内存2*10000000*64/8/1024/1024=152MB，也可以开长度为3的long long数组 $f$ 和 $g$ ，数组不断滚动即可。

#include 
using namespace std;

#define ll long long
#define db double
// #define mod 10000ll
#define mod 1000000007ll

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

int n;
ll f[3], g[3];
int main() {
    scanf("%d", &n);
    f[1] = 1;
    for (int i = 0; i < n; i++) {
        f[2] = (f[2] + f[0]) % mod;
        f[2] = (f[2] + f[1]) % mod;
        f[2] = (f[2] + g[1]) % mod;
        g[2] = (g[2] + f[0] * 2) % mod;
        g[2] = (g[2] + g[1]) % mod;
        for (int i = 0; i < 2; i++) f[i] = f[i + 1], g[i] = g[i + 1];
        g[2] = f[2] = 0;
    }
    cout << f[1];
    return 0;
}

H 扫雷

要考虑到若地雷a能炸地雷b，此时地雷b不一定能炸地雷a，因为地雷a和地雷b的r不一样，所以地雷之间能炸到的关系是有向边。

如何快速找到所有能炸到的地雷？因为r的范围不大，所以我使用的方法是将地雷存了三遍，按id顺序存了一遍，按x坐标顺序存了一遍，按y坐标顺序存了一遍，然后二分x和y上下界（用lower_bound函数），在x和y中找到一个可能符合条件的区间且不会很大，在这两个区间里对于可达节点加入有向边。

而后对于所有排雷火箭，dfs其所有可达地雷，统计可达节点个数

复杂度$O(nlogn+n)$

#include 
using namespace std;

#define ll long long
#define db double
#define maxn 50005

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

struct node {
    ll x, y, id, r;
} a[maxn], by_y[maxn], by_x[maxn];
int xval[maxn], yval[maxn];
int v[maxn];
vector<int> mp[maxn];
int ans, n, m, x, y, r;

bool cmp_y(node a, node b) { return a.y < b.y; }

bool cmp_x(node a, node b) { return a.x < b.x; }

void dfs(int i) {
    v[i] = 1;
    ++ans;
    for (int ii = 0, sz = mp[i].size(); ii < sz; ii++) {
        if (!v[mp[i][ii]]) dfs(mp[i][ii]);
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i++) {
        scanf("%d%d%d", &x, &y, &r);
        by_x[i].x = by_y[i].x = a[i].x = x;
        by_x[i].y = by_y[i].y = a[i].y = y;
        by_x[i].r = by_y[i].r = a[i].r = r;
        by_x[i].id = by_y[i].id = a[i].id = i;
    }
    sort(by_y, by_y + n, cmp_y);
    sort(by_x, by_x + n, cmp_x);
    for (int i = 0; i < n; i++) {
        xval[i] = by_x[i].x;
        yval[i] = by_y[i].y;
    }
    for (int i = 0; i < n; i++) {
        int xl = lower_bound(xval, xval + n, a[i].x - 21) - xval;
        int xr = upper_bound(xval, xval + n, a[i].x + 21) - xval;
        for (int j = xl; j < xr; j++) {
            ll xd = llabs(a[i].x - a[by_x[j].id].x);
            ll yd = llabs(a[i].y - a[by_x[j].id].y);
            // ll rd = a[i].r + a[by_x[j].id].r;
            if (xd * xd + yd * yd <= a[i].r * a[i].r) {
                mp[i].push_back(by_x[j].id);
                // mp[by_x[j].id].push_back(i);
            }
            if (xd * xd + yd * yd <= a[by_x[j].id].r * a[by_x[j].id].r) {
                // mp[i].push_back(by_x[j].id);
                mp[by_x[j].id].push_back(i);
            }
        }
        int yl = lower_bound(yval, yval + n, a[i].y - 11) - yval;
        int yr = upper_bound(yval, yval + n, a[i].y + 11) - yval;
        for (int j = yl; j < yr; j++) {
            ll xd = llabs(a[i].x - a[by_y[j].id].x);
            ll yd = llabs(a[i].y - a[by_y[j].id].y);
            // ll rd = a[i].r + a[by_y[j].id].r;
            if (xd * xd + yd * yd <= a[i].r * a[i].r) {
                mp[i].push_back(by_y[j].id);
                // mp[by_x[j].id].push_back(i);
            }
            if (xd * xd + yd * yd <= a[by_y[j].id].r * a[by_y[j].id].r) {
                // mp[i].push_back(by_x[j].id);
                mp[by_y[j].id].push_back(i);
            }
        }
    }
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d", &x, &y, &r);
        int xl = lower_bound(xval, xval + n, x - 11) - xval;
        int xr = upper_bound(xval, xval + n, x + 11) - xval;
        for (int j = xl; j < xr; j++) {
            ll xd = llabs(x - a[by_x[j].id].x);
            ll yd = llabs(y - a[by_x[j].id].y);
            // ll rd = r + a[by_x[j].id].r;
            if (xd * xd + yd * yd <= r * r) {
                if (!v[by_x[j].id]) dfs(by_x[j].id);
            }
        }
        int yl = lower_bound(yval, yval + n, y - 11) - yval;
        int yr = upper_bound(yval, yval + n, y + 11) - yval;
        for (int j = yl; j < yr; j++) {
            ll xd = llabs(x - a[by_y[j].id].x);
            ll yd = llabs(y - a[by_y[j].id].y);
            // ll rd = r + a[by_y[j].id].r;
            if (xd * xd + yd * yd <= r * r) {
                if (!v[by_y[j].id]) dfs(by_y[j].id);
            }
        }
    }
    printf("%d", ans);
    return 0;
}

I 李白打酒加强版

用搜索+剪枝的方法可以过40%样例，正解是动态规划

$d_{i,j,k}$表示从店剩余n次，花剩余m次，酒有2斗到店还剩余i次，花还剩余j次，酒还剩余k斗有几种变换方法。

所以初始状态$d_{n,m,2}=1$，答案是$d_{0,0,0}$

复杂度 $O(100nm)$，最多不超过$100\ast 100\ast 100$

#include 
using namespace std;

#define ll long long
#define db double
#define mod 1000000007ll

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

ll ans;

// 一开始写了个搜索
// n：店的剩余次数 m：花的剩余次数 val：酒的余量 op：上一步操作
void dfs(int n, int m, ll val, int op) {
    if (!n && !m) {
        if (val == 0 && op == 0) ans = (ans + 1) % mod; //保证上一步是花
        return;
    }
    if (n && val * 2 <= m) dfs(n - 1, m, val * 2, 1); // 走店
    if (m && val) dfs(n, m - 1, val - 1, 0); // 走花
}

ll d[105][105][105];
int n, m;
int main() {
    // cout<<25*0.6;
    cin >> n >> m;
    d[n][m][2] = 1;
    for (int i = n; i >= 0; i--) {// 枚举酒的剩余次数
        for (int j = m; j >= 0; j--) {// 枚举花的剩余次数
            if (i == n && j == m) continue;
            for (int k = 0; k <= 100; k++) {// 枚举酒的余量
            	// 花还有剩余 保证最后一步是花 同时酒余量是偶数 可以从k/2转移过来
                if (j != 0 && i + 1 <= n && !(k & 1)) 
                    d[i][j][k] = (d[i][j][k] + d[i + 1][j][k / 2]) % mod;
                if (j + 1 <= m)
                    d[i][j][k] = (d[i][j][k] + d[i][j + 1][k + 1]) % mod;
            }
        }
    }
    cout << d[0][0][0];
    // dfs(n,m,2,0);
    // cout<
    return 0;
}

J 砍竹子

通过打表发现，每个数字通过题目所述的变换，最多变换4次即可变为1。

我的解法是，每个数字开一个栈（stack），将每个数字不断变换放入对应位置的栈中，最小的数字在栈顶，最初的数字在栈底，所以一段能变换的数字，其栈顶都是相同的，我们就可以不断模拟这个过程，统计出答案。此求平方根可能存在精度误差

复杂度大概$O(nlogn)$

（代码写的很丑 谢谢看到这的xdm

#include 
using namespace std;

#define ll long long
#define db double
#define maxn 200005

ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, b % a); }

int n;
ll a[maxn];
stack<ll> mp[maxn];
ll num = 0;
int ans = 0;

void merge(int idx, int cnt) {
    // cout<
    int flag = 0;
    for (int i = idx - cnt; i < idx; i++) {
        mp[i].pop();
        flag = 1;
        --num;
    }
    if (flag) ++ans;
}

ll _sqrt(ll a) {
    a=a/2+1;
    ll l = 1, r = 1000000005, ret = 1;
    while (l <= r) {
        ll mid = l + r >> 1;
        if (mid * mid <= a) {
            ret = mid;
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return ret;
}

int main() {
    // for (ll a = 1000000000000000000, idx = 0; idx < 10;
    //      a -= 100000000000000, idx++) {
    //     ll tmp = a;
    //     while (tmp > 1) {
    //         cout << tmp << ' ';
    //         tmp = _sqrt(tmp / 2 + 1);
    //         cout << "{" << (tmp * tmp - 1) * 2 << "} ";
    //     }
    //     cout << '\n';
    // }
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%lld", &a[i]);
        ll tmp = a[i];
        while (tmp > 1) {
            // cout<
            mp[i].push(tmp);
            ++num;
            // tmp=sqrt(tmp/2+1);
            tmp = _sqrt(tmp);
        }
        // cout<<'\n';
    }
    while (num) {
        // cout<<"######### "<
        for (ll i = 0, la = -1, cnt = 0; i < n; i++) {
            // cout<<"{"<
            if (!mp[i].empty()) {
                if (la == mp[i].top()) {
                    cnt++;
                } else {
                    merge(i, cnt);
                    la = mp[i].top();
                    cnt = 1;
                }
            } else {
                // cout<<"empty\n";
                merge(i, cnt);
                la = -1;
                cnt = 0;
            }
            // cout<
            if (i == n - 1) {
                merge(i + 1, cnt);
                cnt = 0;
                la = -1;
            }
        }
    }
    printf("%d", ans);
    return 0;
}