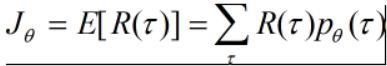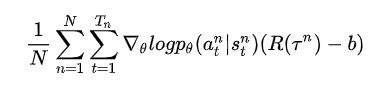01 强化学习——策略梯度法(Policy Gradient PG)（离散动作）

一、来源和定位

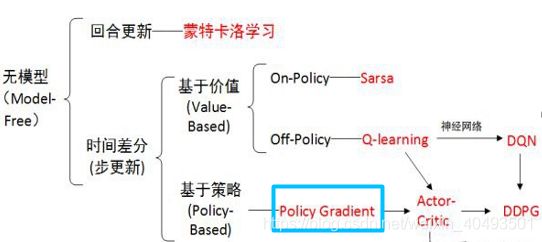
1.1 PG算法在强化学习方法中的定位

策略梯度是基于策略搜索方法中最基础的方法，要理解AC，DDPG需要先学习策略梯度。

策略梯度方法就是将策略参数化，寻找最优的参数，使总体收益最大。关键在如何将策略参数化。

 

1.2 策略梯度直观理解

策略的表示

一般将策略表示为状态的函数：，

对于离散动作来说是一种随机分布：，随机策略参数化即为参数化这种分布。

对于连续动作来说是随机高斯策略，用高斯策略来表示这种分布，参数化的方法为参数化高斯分布的均值和方差。

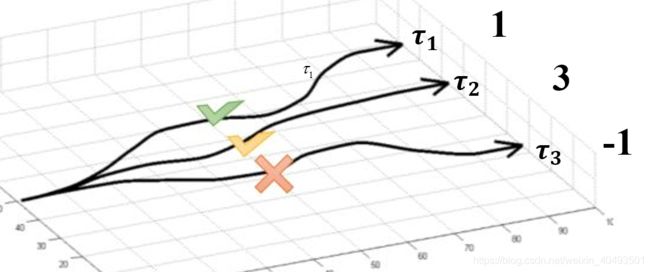
策略梯度是将智能体的策略转换成参数的非线性函数，通过寻优参数找到函数的最值，从而使回报值最大。如下图所示，假设有三条路径（每一条路径理解为一个策略）回报分别为1,3，-1.最直观的做法是尽量选择第二条路径，即增加该策略的概率，使最终的回报最大。

二、问题数学表示

2.1 误差

主要思想是使最终的回报最大，即一个完成的交互episode（从初始状态到最终状态的一个策略）。

目标：【一条完整的episode的回报期望最大】

要使该目标最大，则参数的更新方向为梯度上升的方向。

此公式中有两点需要注意，第一是上式第三行的变换，该方法在梯度中经常使用，直接记住即可，第二是最后一等式的变换，是概率，与累加和可以看成是求后面部分的期望

策略产生的轨迹如下：，则该轨迹的概率可以用联合概率来表示：

注意上式中只有与有关，其他均无关，因此对其去对数并求导可以转化为：

当采样了N条轨迹，（在程序中一条完整轨迹为一个episode），目标梯度可以用下面式子表示：

到此为止我们找到了误差的梯度，由此来构建神经网络的误差。

目标------>目标的梯度------>误差梯度------>误差------>编程实现

2.2 基线

在对动作进行采样时，无法保证每个动作都能抽取到，如果R都是正值，则每个动作的概率都会增大，对每抽取到的动作不公平，将上式减去一个值，保证其均值不变，梯度如下所示：

三、代码实现

3.1 源代码

import numpy as np
import tensorflow as tf

# reproducible
np.random.seed(1)
tf.set_random_seed(1)


class PolicyGradient:
    def __init__(self,n_actions,n_features,learning_rate=0.01,reward_decay=0.95,output_graph=False,):
        self.n_actions = n_actions
        self.n_features = n_features
        self.lr = learning_rate
        self.gamma = reward_decay   # 回报折扣因子

        self.ep_obs, self.ep_as, self.ep_rs = [], [], []

        self._build_net()

        self.sess = tf.Session()

        if output_graph:
            # $ tensorboard --logdir=logs
            # http://0.0.0.0:6006/
            # tf.train.SummaryWriter soon be deprecated, use following
            tf.summary.FileWriter("logs/", self.sess.graph)

        self.sess.run(tf.global_variables_initializer())

    def _build_net(self):
        with tf.name_scope('inputs'):
            self.tf_obs = tf.placeholder(tf.float32, [None, self.n_features], name="observations")
            self.tf_acts = tf.placeholder(tf.int32, [None, ], name="actions_num")
            self.tf_vt = tf.placeholder(tf.float32, [None, ], name="actions_value")
        # fc1
        layer = tf.layers.dense(
            inputs=self.tf_obs,
            units=10,
            activation=tf.nn.tanh,  # tanh activation
            kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
            bias_initializer=tf.constant_initializer(0.1),
            name='fc1'
        )
        # fc2
        all_act = tf.layers.dense(
            inputs=layer,
            units=self.n_actions,
            activation=None,
            kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
            bias_initializer=tf.constant_initializer(0.1),
            name='fc2'
        )

        self.all_act_prob = tf.nn.softmax(all_act, name='act_prob')  # use softmax to convert to probability

        with tf.name_scope('loss'):
            # to maximize total reward (log_p * R) is to minimize -(log_p * R), and the tf only have minimize(loss)
            neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=all_act, labels=self.tf_acts)   # this is negative log of chosen action
            # or in this way:
            # neg_log_prob = tf.reduce_sum(-tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions), axis=1)
            loss = tf.reduce_mean(neg_log_prob * self.tf_vt)  # reward guided loss

        with tf.name_scope('train'):
            self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)

    def choose_action(self, observation):
        prob_weights = self.sess.run(self.all_act_prob, feed_dict={self.tf_obs: observation[np.newaxis, :]})
        action = np.random.choice(range(prob_weights.shape[1]), p=prob_weights.ravel())  # select action w.r.t the actions prob
        return action

    def store_transition(self, s, a, r):
        self.ep_obs.append(s)
        self.ep_as.append(a)
        self.ep_rs.append(r)

    def learn(self):
        # discount and normalize episode reward
        discounted_ep_rs_norm = self._discount_and_norm_rewards()

        # train on episode
        self.sess.run(self.train_op, feed_dict={
             self.tf_obs: np.vstack(self.ep_obs),  # shape=[None, n_obs]
             self.tf_acts: np.array(self.ep_as),  # shape=[None, ]
             self.tf_vt: discounted_ep_rs_norm,  # shape=[None, ]
        })

        self.ep_obs, self.ep_as, self.ep_rs = [], [], []    # empty episode data
        return discounted_ep_rs_norm

    def _discount_and_norm_rewards(self):
        # discount episode rewards
        discounted_ep_rs = np.zeros_like(self.ep_rs)
        running_add = 0
        for t in reversed(range(0, len(self.ep_rs))):
            running_add = running_add * self.gamma + self.ep_rs[t]
            discounted_ep_rs[t] = running_add

        # normalize episode rewards   # 注意此处将R_tao - b
        discounted_ep_rs -= np.mean(discounted_ep_rs)
        discounted_ep_rs /= np.std(discounted_ep_rs)
        return discounted_ep_rs


import gym
# from RL_brain import PolicyGradient
import matplotlib.pyplot as plt

DISPLAY_REWARD_THRESHOLD = -2000  # renders environment if total episode reward is greater then this threshold
# episode: 154   reward: -10667
# episode: 387   reward: -2009
# episode: 489   reward: -1006
# episode: 628   reward: -502

RENDER = False  # rendering wastes time

episode_num = 100

env = gym.make('MountainCar-v0')
env.seed(1)     # reproducible, general Policy gradient has high variance
env = env.unwrapped

print(env.action_space)
print(env.observation_space)
print(env.observation_space.high)
print(env.observation_space.low)

RL = PolicyGradient(
    n_actions=env.action_space.n,
    n_features=env.observation_space.shape[0],
    learning_rate=0.02,
    reward_decay=0.995,
    # output_graph=True,
)

for i_episode in range(episode_num):

    observation = env.reset()

    while True:
        if RENDER: env.render()

        action = RL.choose_action(observation)

        observation_, reward, done, info = env.step(action)     # reward = -1 in all cases

        RL.store_transition(observation, action, reward)

        if done:
            # calculate running reward
            ep_rs_sum = sum(RL.ep_rs)
            if 'running_reward' not in globals():
                running_reward = ep_rs_sum
            else:
                running_reward = running_reward * 0.99 + ep_rs_sum * 0.01
            if running_reward > DISPLAY_REWARD_THRESHOLD: RENDER = True     # rendering

            print("episode:", i_episode, "  reward:", int(running_reward))

            vt = RL.learn()  # train

            if i_episode == 30:
                plt.plot(vt)  # plot the episode vt
                plt.xlabel('episode steps')
                plt.ylabel('normalized state-action value')
                plt.show()

            break

        observation = observation_

3.2 重点理解

neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=all_act, labels=self.tf_acts)

其中，all_act为网络的输出，self.tf_acts为标签的索引(比如第6个动作就是self.tf_acts=6)。
这个损失函数先把logits部分取sotfmax，之后又把label变为one-hot的形式并做Cross-Entropy，算完之后的结果就是第n个  的第t个state选择的action的negative log。
即：neg_log_prob=  。
再loss = tf.reduce_mean(neg_log_prob * self.tf_vt)，得到：