互补格雷码+相移码求解包裹相位（Matlab实现）

说明

​ 采用4幅相移图+5幅格雷码图+1幅全黑+1幅全白共11张图像，详细原理参考：(超详细)互补格雷码+相移码求解包裹相位（Python实现）。这次Matlab程序有一些改变，比之前增加了两幅图片(1幅全黑+1幅全白)：用来生成掩码来提取感兴趣区域。程序运行速度很慢（甚至有点离谱），主要原因在于5、求解格雷码值这一块代码没有优化，只是暴力循环遍历每个像素，大家有好的优化方法可以交流一下。

代码

clc, clear, close all
% ==========================1、设置数据文件夹路径===================================
dataPath = './data/';                                   % 数据文件夹为当前路径下的data目录
imagePath = strcat(dataPath, 'David');                  % 子目录为data文件夹下的David文件夹
addpath(genpath(dataPath));                             % 加入MATLAB路径
imageFile = dir(fullfile(imagePath, '*.Bmp'));          % 照片格式为Bmp
imgeFileNames = {imageFile.name};

% ==========================2、格雷码===============================================
% 格雷码
grayCode = containers.Map(...                               %建立一般格雷码与对应十进制数的映射关系
    {'0000', '0001', '0011', '0010', '0110', '0111', '0101', '0100', '1100', '1101', '1111', '1110', '1010', '1011', '1001', '1000'}, ...
    {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15});%k1值

% 互补的格雷码
complementaryGrayCode = containers.Map(...                  %建立互补格雷码与对应十进制数的映射关系
    {'00000', '00001', '00011', '00010', '00110', '00111', '00101', '00100', ... 
     '01100', '01101', '01111', '01110', '01010', '01011', '01001', '01000', ... 
     '11000', '11001', '11011', '11010', '11110', '11111', '11101', '11100', ...
     '10100', '10101', '10111', '10110', '10010', '10011', '10001', '10000'}, ...
    {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31});%k2值

% ==========================3、读取图片=============================================
% 掩码图像
imageWhite = imread( imgeFileNames{1} );              %全亮图案
imageBlack = imread( imgeFileNames{2} );              %全黑图案
imageMask = imbinarize(imageWhite - imageBlack);
figure; set(gcf, 'Name', '掩码图像');imshow(imageMask); title('掩码图像');

% 被物体调制的四步相移正弦条纹
x0 = double((imread( imgeFileNames{8} )));
x1 = double((imread( imgeFileNames{9} )));
x2 = double((imread( imgeFileNames{10} )));
x3 = double((imread( imgeFileNames{11} )));
[row, col] = size(x1); 
figure; set(gcf, 'Name',  '被物体调制的四步相移正弦条纹');
subplot(221); imshow(x0, []); title('相移：0');
subplot(222); imshow(x1, []); title('相移：pi/2');
subplot(223); imshow(x2, []); title('相移：pi');
subplot(224); imshow(x3, []); title('相移：pi*3/2');

% 被物体调制的格雷条纹
T = round(getThershold(x0,x1,x2,x3));                 %计算二值化阈值
y0 = binarization(imread( imgeFileNames{3} ) , T, imageMask);
y1 = binarization(imread( imgeFileNames{4} ) , T, imageMask);
y2 = binarization(imread( imgeFileNames{5} ) , T, imageMask);
y3 = binarization(imread( imgeFileNames{6} ) , T, imageMask);
y4 = binarization(imread( imgeFileNames{7} ) , T, imageMask);
figure; set(gcf,'Name','阈值图');
imshow(T, []); 
figure; set(gcf,'Name','被物体调制的格雷码条纹');
subplot(321); imshow(y0, []); title('格雷码1');
subplot(322); imshow(y1, []); title('格雷码2');
subplot(323); imshow(y2, []); title('格雷码3');
subplot(324); imshow(y3, []); title('格雷码4');
subplot(325); imshow(y4, []); title('格雷码5');

% ==========================4、求解相对相位================================
wrappedPhase = getwrappedphase(x0,x1,x2,x3,imageMask);     
wrappedPhaseShow = wrappedPhase./(2*pi);                         %放缩显示                                             
figure; set(gcf,'Name','相对相位');
imshow(wrappedPhaseShow, []); title('相对相位'); 

% ==========================5、求解格雷码值================================
k1 = zeros(row,col);
k2 = zeros(row,col);
for i = 1:row
    for j = 1:col
        if imageMask(i,j) == 1
            %下面这一行代码可以替换使用getGrayStr()函数获得的v1
            %v1 = string(num2str(y0(i,j)),num2str(y1(i,j)),num2str(y2(i,j)),num2str(y3(i,j))); 
            v1 = getGrayStr(y0(i,j),y1(i,j),y2(i,j),y3(i,j));
            v2 = strcat(v1,num2str(y4(i,j)));
            k1(i, j) = grayCode(v1);
            k2(i, j) = floor((complementaryGrayCode(v2)+1)/2);
        end
    end
end
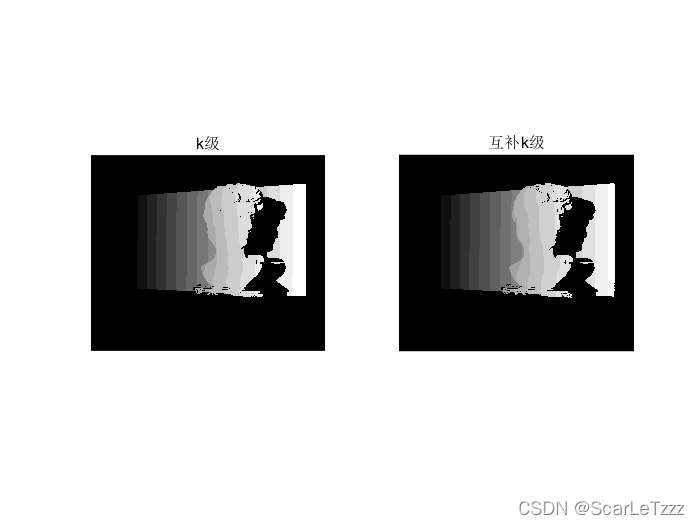
figure; set(gcf, 'Name', '相位展开叠加k*2*pi');
subplot(121); imshow(k1, []); title('k级');
subplot(122); imshow(k2, []); title('互补k级');

% ==========================6、求解绝对相位================================
unwrappedPhase = getunwrappedphase(wrappedPhase,k1,k2,row,col,imageMask);
unwrappedPhaseShow = unwrappedPhase./(32*pi);                     %放缩显示
figure; set(gcf,'Name','绝对相位');
imshow(unwrappedPhaseShow, []); title('绝对相位'); 

% ==========================7、保存结果=============================================
save PhaseDecodeResult;


%==========================辅助函数===============================================
%获取二值化阈值
function [T] = getThershold(i1,i2,i3,i4)
T = (i1+i2+i3+i4)/4;
end

%逐点二值化
function [binarizedImage]=binarization(I,thershold,imageMask)
[row,col]=size(I);
binarizedImage=zeros(row,col);
for i = 1:row
    for j = 1:col
        if imageMask(i,j) == 1
            if I(i,j) < thershold(i,j)
                binarizedImage(i,j) = 0;
            else
                binarizedImage(i,j) = 1;
            end
        end
    end
end
end

%包裹相位求解算法
function[wrappedPhase] = getwrappedphase(x0,x1,x2,x3,imageMask)
[row, col] = size(x1);
wrappedPhase = zeros(row, col);
for i = 1:row
    for j = 1:col
        if imageMask(i, j) == 1
            if x0(i,j) == x2(i,j) && x1(i, j) > x3(i,j)
                wrappedPhase(i, j) = 0;
            elseif x0(i,j) > x2(i,j) && x1(i, j) == x3(i,j)
                wrappedPhase(i, j) = pi/2;
            elseif x0(i,j) == x2(i,j) && x1(i, j) < x3(i,j)
                wrappedPhase(i, j) = pi;
            elseif x0(i,j) < x2(i,j) && x1(i, j) == x3(i,j)
                wrappedPhase(i, j) = 3*pi/2;
            elseif x0(i,j) > x2(i,j) && x1(i, j) > x3(i,j)
                wrappedPhase(i, j) = atan((x0(i,j)-x2(i,j))/(x1(i,j)-x3(i,j)));
            elseif x0(i,j) > x2(i,j) && x1(i, j) < x3(i,j)
                wrappedPhase(i, j) = pi  - atan((x0(i,j)-x2(i,j))/(x3(i,j)-x1(i,j)));              
            elseif x0(i,j) < x2(i,j) && x1(i, j) < x3(i,j)
                wrappedPhase(i, j) = pi  + atan((x0(i,j)-x2(i,j))/(x1(i,j)-x3(i,j)));              
            elseif x0(i,j) < x2(i,j) && x1(i, j) > x3(i,j)
                wrappedPhase(i, j) = 2*pi  - atan((x2(i,j)-x0(i,j))/(x1(i,j)-x3(i,j)));           
            end
        end
    end
end
end

%获得格雷码字符串
function [v1]=getGrayStr(g0,g1,g2,g3)
g = num2str(g0*1000 + g1*100 + g2*10 + g3)
addition1 = '0'; addition2 = '00'; addition3 = '000';
if length(g) == 1
    v1 = strcat(addition3,g);
elseif length(g) == 2
    v1 = strcat(addition2,g);
elseif length(g) == 3
    v1 = strcat(addition1,g);
else
    v1 = g;
end
end

%绝对相位求解算法
function[unwrappedPhase] = getunwrappedphase(wrappedPhase,k1,k2,row,col,imageMask)
unwrappedPhase = zeros(row, col);
for i = 1:row
    for j = 1:col
        if imageMask(i, j) == 1
            if wrappedPhase(i,j) <= pi/2
                unwrappedPhase(i,j) = wrappedPhase(i,j) + k2(i,j)*2*pi;
            elseif  wrappedPhase(i,j) > pi/2  &&  wrappedPhase(i,j) < 3*pi/2
                unwrappedPhase(i,j) = wrappedPhase(i,j) + k1(i,j)*2*pi;
            elseif wrappedPhase(i,j) >= 3*pi/2
                unwrappedPhase(i,j) = wrappedPhase(i,j) + (k2(i,j)-1)*2*pi;
            end
        end
    end
end
end

效果图

1、掩码图像

2、调制相移图

3、阈值图

4、二值化格雷码图

5、相对相位图

6、格雷码k级次图

7、绝对相位图