数据结构 树与二叉树 笔记合集(C语言)完结
文章中其实有很多图来帮助理解,但是因为外链的原因,我电脑上的图不能直接拉过来,要完整版的可以评论我直接发PDF版本。个人笔记,仅供参考。
树与二叉树
-
- 树
-
- 常考考点
- 二叉树
- 二叉树的顺序存储
- 二叉树的链式存储
- 二叉树的遍历
-
-
- 二叉树的层次遍历
- 线索二叉树
-
- 找中序前驱
- 中序线索化
- 先序线索化
- 后序线索化
- 中序线索二叉树找中序后继
- 中序线索二叉树找中序前驱
- 先序线索二叉树找先序后继
- 先序线索二叉树找先序前驱
-
- 树的存储结构
-
- 双亲表示法(顺序存储)
- 孩子表示法(顺序+链式存储)
- 孩子兄弟表示法(链式存储) C
- 树的层次遍历(广度优先遍历)
- 树的先根、后根遍历(深度优先遍历)
- 二叉排序树(BST Binary Search Tree)
-
- 二叉排序树的查找
-
- 循环结构实现
- 递归结构实现
- 二叉排序树的插入
-
- 循环结构实现
- 递归结构实现
- 二叉排序树的构造
- 二叉排序树的删除
- 查找效率分析
- 平衡二叉树
-
- 定义
- 调整最小不平衡子树
-
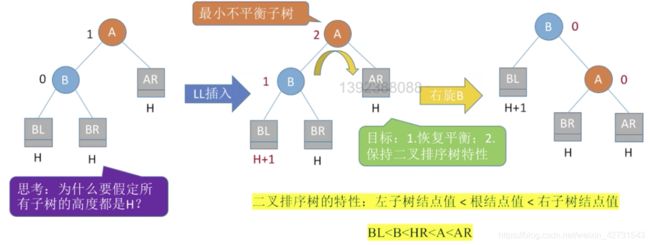
- 调整1(LL)
- 调整2(RR)
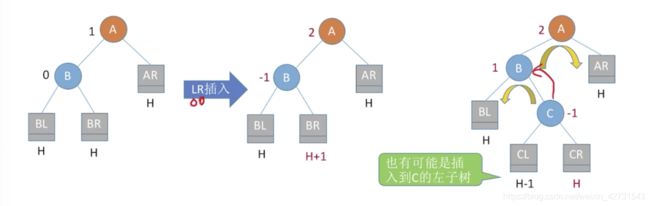
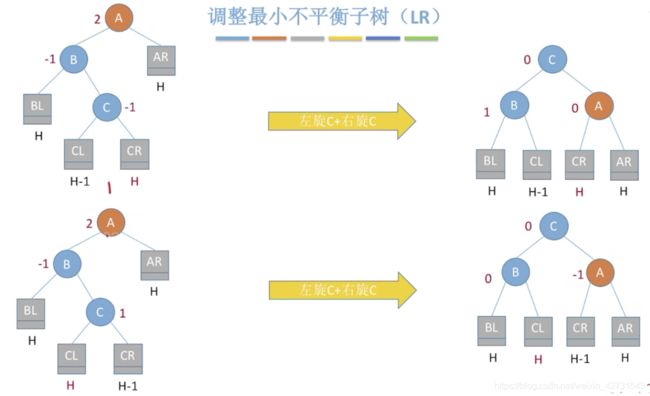
- 调整3(LR)
- 调整4(RL)
- 查找效率分析
- 哈夫曼树
-
- 带权路径长度
- 哈夫曼树的定义(Huffman Tree)
- 哈夫曼树的构造
树
·结点之间的路径只能从上往下
·结点的度:结点的分支数
·树的度:树中各节点的度的最大值
常考考点
- 结点数 = 总度数 + 1(根结点的头上没有分支);
- 度为m的树、m叉树的区别;
- 度为m的树第i层至多有 m i − 1 m^{i-1} mi−1个结点(i >= 1),m叉树第i层至多有 m i − 1 m^{i-1} mi−1个结点(i >= 1);
- 高度为h的m叉树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1个结点(等比数列求和);
- 高度为h的m叉树至少有h个结点,高度为h、度为m的树至少有h+m-1个结点;
- 具有n个结点的m叉树的最小高度为 ⌈ log m ( n ( m − 1 ) + 1 ) ⌉ \lceil\log_m(n(m-1)+1)\rceil ⌈logm(n(m−1)+1)⌉
二叉树
1.满二叉树 2.完全二叉树 3.二叉排序树 4.平衡二叉树
常考考点:
- 设非空二叉树中度为0、1和2度结点个数分别为 n 0 、 n 1 n_0、n_1 n0、n1和 n 2 n_2 n2,则 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1
- 二叉树第i层至多有 2 i − 1 2^{i-1} 2i−1个结点(i >= 1)
- 高度为h的二叉树至多有 2 h − 1 2^h - 1 2h−1个结点
- 具有n个(n>0)结点的完全二叉树的高度h为 ⌈ log 2 ( n + 1 ) ⌉ \lceil\log_2(n+1)\rceil ⌈log2(n+1)⌉或 ⌊ log 2 n ⌋ + 1 \lfloor\log_2n\rfloor+1 ⌊log2n⌋+1
5 对于完全二叉树,可以由结点数n推出度为0、1和2的结点个数 n 0 、 n 1 n_0、n_1 n0、n1和 n 2 n_2 n2
二叉树的顺序存储
#define MaxSize 100
struct TreeNode{
ElemType value; //结点中的数据元素
bool isEmpty; //结点是否为空
};
TreeNode t[MaxSize];
//初始化
for (int i=0; i<MaxSize; i++){
t[i].isEmpty = true;
}
对于完全二叉树:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9xzA6fog-1585843866454)(/Users/zyairelu/Library/Application%20Support/typora-user-images/Screen%20Shot%202020-04-01%20at%207.00.09%20PM.png)]
二叉树的链式存储
struct ElemType{
int value;
};
typedef struct BiTNode{
ElemType data; //数据域
struct BiTNode *lchild, *rchild; //左、右孩子指针
struct BiTNode *parent; //父结点指针
}BiTNode, *BiTree;
//定义一棵空树
BiTree root = NULL;
//插入根结点
root = (BiTree)malloc(sizeof(BiTNode));
root -> data = {1};
root -> lchild = NULL;
root -> rchild = NULL;
//插入新结点
BiTNode * p = (BiTNode *)malloc(sizeof(BiTNode));
p -> data = {2};
p -> lchild = NULL;
p -> rchild = NULL;
root -> lchild = p; //作为根结点的左孩子
· n个结点的二叉链表共有n+1个空链域
二叉树的遍历
- 先序遍历:根左右(NLR)
- 中序遍历:左根右(LNR)
- 后序遍历:左右根(LRN)
二叉树的层次遍历
算法思想:
· 初始化一个辅助队列;
·根结点入队;
·若队列非空,则队头结点出队,访问该结点,并将其左、右孩子插入队尾(如果有的话)
·重复第三步直至队列为空
线索二叉树
找中序前驱
//中序遍历
void FindPre(BiTree T){
if (T != NULL){
FindPre(T -> lchild); //递归遍历左子树
visit(T); //访问根结点
FindPre(T -> rchild); //递归遍历右子树
}
}
//访问结点q
void visit(BiTNode *q){
if (q == p) //当前访问结点刚好是结点p
final = pre; //找到p的前驱
else
pre = q; //pre指向点钱访问的结点
}
//辅助全局变量,用于查找结点p的前驱
BiTNode *p; //p指向目标结点
BiTNode *pre = NULL; //指向当前访问结点的前驱
BiTNode *final = NULL; //用于记录最终结果
中序线索化
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre = NULL;
//中序线索化二叉树
void CreateInThread(ThreadTree T){
pre = NULL; //pre初始为NULL
if (T != NULL){ //非空二叉树才能线索化
InThread(T); //中序线索化二叉树
if (pre -> rchild == NULL)
pre -> rtag = 1; //处理遍历的最后一个结点
}
}
//线索二叉树结点
typedef struct ThreadNode{
ElemType data; //数据域
struct BiTNode *lchild, *rchild; //左、右孩子指针
int ltag, rtag; //左、右线索标志
}ThreadNode, *ThreadTree;
//中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T){
if (T != NULL){
InThread(T -> lchild);
visit(T);
InThread(T -> rchild);
}
}
void visit(ThreadNode *q){
if (q -> lchild == NULL){
q -> lchild = pre;
q -> ltag = 1;
}
if (pre != NULL && pre -> rchild == NULL){
pre -> rchild = q;
pre -> rtag = 1;
}
pre = q;
}
先序线索化
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre = NULL;
//中序线索化二叉树
void CreateInThread(ThreadTree T){
pre = NULL; //pre初始为NULL
if (T != NULL){ //非空二叉树才能线索化
InThread(T); //中序线索化二叉树
if (pre -> rchild == NULL)
pre -> rtag = 1; //处理遍历的最后一个结点
}
}
//线索二叉树结点
typedef struct ThreadNode{
ElemType data; //数据域
struct BiTNode *lchild, *rchild; //左、右孩子指针
int ltag, rtag; //左、右线索标志
}ThreadNode, *ThreadTree;
//先序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T){
if (T != NULL){
visit(T);
if (T -> ltag == 0) //important! 判断lchild不是前驱线索
InThread(T -> lchild);
InThread(T -> rchild);
}
}
void visit(ThreadNode *q){
if (q -> lchild == NULL){
q -> lchild = pre;
q -> ltag = 1;
}
if (pre != NULL && pre -> rchild == NULL){
pre -> rchild = q;
pre -> rtag = 1;
}
pre = q;
}
后序线索化
同上理
中序线索二叉树找中序后继
//找到以p为根的子树中,第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p){
//循环找到最左下结点(不一定是叶结点)
while(p->ltag == 0) p = p->lchild;
return p;
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p){
//右子树中最左下结点
if (p->rtag == 0) return Firstnode(p->rchild);
else return p->rchild; //rtag == 1直接返回后继线索,即是中序后继
}
//对中序线索二叉树进行中序遍历 (利用线索实现的非递归算法 空间复杂度O(1))
void Inorder(ThreadNode *T){
for(ThreadNode *p = Firstnode(T); p != NULL; p = Nextnode(p))
visit(p);
}
中序线索二叉树找中序前驱
//找到以p为根的子树中,最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p){
//循环找到最左下结点(不一定是叶结点)
while(p->rtag == 0) p = p->rchild;
return p;
}
//在中序线索二叉树中找到结点p的前驱结点
ThreadNode *Prenode(ThreadNode *p){
//左子树中最右下结点
if (p->ltag == 0) return Lastnode(p->lchild);
else return p->lchild; //rtag == 1直接返回前驱线索,即是中序前驱
}
//对中序线索二叉树进行逆向中序遍历 (利用线索实现的非递归算法 空间复杂度O(1))
void Inorder(ThreadNode *T){
for(ThreadNode *p = Lastnode(T); p != NULL; p = Prenode(p))
visit(p);
}
先序线索二叉树找先序后继
//在先序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p){
//若p有左孩子,则先序后继为左孩子,否则为右孩子
//若均无,则为它自己,表明为最后一个结点
if (p->lchild != 0) return p->lchild;
else if (p->rchild != 0) return p->rchild;
else return p;
}
//对先序线索二叉树进行中序遍历,根结点为起始
void Inorder(ThreadNode *T){
for(ThreadNode *p = root; p != NULL; p = Nextnode(p))
visit(p);
}
先序线索二叉树找先序前驱
只有知道p的父结点,才可以找到先序前驱。
后序线索二叉树与先序线索二叉树找前驱后继相似。
树的存储结构
双亲表示法(顺序存储)
#define MAX_TREE_SIZE 100 //树中最多结点
typedef struct{ //树的结点定义
ElemType data; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MAX_TREE_SIZE]; //双亲表示
int n; //结点数
}PTree;
孩子表示法(顺序+链式存储)
struct CTnode{
int child; //孩子结点在数组中的位置
struct CTNode *next; //下一个孩子
};
typedef struct{
CTBox nodes[MAX_TREE_SIZE];
int n, r; //结点数和根的位置
}CTree;
孩子兄弟表示法(链式存储) C
typedef struct CSNode{
ElemType data; //数据域
struct CSNode *firstchild, *nextsibling; //第一个孩子和右兄弟指针
}CSNode, *CSTree;
树的层次遍历(广度优先遍历)
用队列实现:
- 若树非空,则根结点入队;
- 若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队;
- 重复2直到队列为空
树的先根、后根遍历(深度优先遍历)
树的后根遍历序列与这棵树相应的二叉树的中序序列相同。
二叉排序树(BST Binary Search Tree)
左子树结点值 < 根结点值 < 右子树结点值
=> 用中序遍历后,可以得到一个递增的有序序列
二叉排序树的查找
循环结构实现
//二叉排序树结点
typeof struct BSTNode{
int key;
struct BSTNode *lchild, *rchild;
}BSTNode, BSTree;
//在二叉排序树中查找值为key的结点
BSTNode *BST_Search(BSTree T, int key){
while(T != NULL && key != T->key){ //若树空或等于key的值,则结束
if (key < T->key) T = T->lchild; //小于,则在左子树上查找
else T = T->rchild; //大于,则在右子树上查找
}
return T;
}
递归结构实现
BSTNode *BSTSearch(BSTree T, int key){
if (T == NULL)
return NULL; //查找失败
if (key == T->key)
return T; //查找成功,返回结点T
else if (key < T->key)
return BSTSearch(T->lchild. key); //在左子树中查找
else
return BSTSearch(T->rchild, key); //在右子树中查找
}
二叉排序树的插入
循环结构实现
BSTNode *BST_Insert(BSTree &T, int key){
while(T->key != NULL){
if (T->key == key) //已经存在了该值,则插入失败
return 0;
else if (T->key < key) //左子树
T = T->lchild;
else
T = T->rchild;
}
T->key = key;
return 1; //插入成功
}
递归结构实现
递归实现,最坏空间复杂度为O(h),h为深度。
int BST_Insert(BSTree &T, int k){
if (T == NULL){ //原树为空,新插入的结点即为根结点
T = (BSTree)malloc(sizeof(BSTNode));
T->key = k;
T->lchild = NULL;
T->rchild = NULL;
return 1; //返回1,则插入成功
}
else if (k == T->key) //原树中已经存在了相应的值,则插入失败
return 0;
else if (k < T->key) //插入到左子树
return BST_Insert(T->lchild, k);
else //插入到右子树
return BST_Insert(T->rchild, k);
}
二叉排序树的构造
//按照 str[]中关键字序列建立二叉排序树
void Creat_BST(BSTree &T, int str[], int n){
T = NULL; //初始时T为空树
int i = 0;
while (i < n){
BST_Insert(T, str[i]);
i++;
}
}
//举个例子
void main(){
str = [13, 15, 8, 5, 9, 12];
int n = sizeof(str);
BSTree T;
Creat_BST(&T, str, n); //over
}
值得注意的是,具有相同元素的str,因素顺序的不同排列可能会产生相同或不相同的二叉排序树。
二叉排序树的删除
- 若被删除结点z是叶结点,则直接删除;
- 若结点z只有一棵左子树或一棵右子树,则让z的子树成为z父结点的子树,替代z的位置;
- 若结点z有左、右两棵子树,则令z的直接后继(或直接前驱)替代z,然后从二叉排序树中删去这个替代本体[左子树的最大值或者右子树的最小值],然后再按照1,2步的方法继续。
查找效率分析
查找成功的平均查找长度 ASL(Average Search Length)
A S L = 每 个 结 点 查 找 长 度 之 和 结 点 总 数 ASL = \frac{每个结点查找长度之和}{结点总数} ASL=结点总数每个结点查找长度之和
查找失败的平均查找长度 ASL(Average Search Length)
A S L = 每 个 空 叶 结 点 查 找 长 度 之 和 空 叶 结 点 总 数 ASL = \frac{每个空叶结点查找长度之和}{空叶结点总数} ASL=空叶结点总数每个空叶结点查找长度之和
平衡二叉树
定义
平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树)——树上任一结点的左子树和右子树的高度之差不超过1。
结点的平衡因子 = 左子树高 - 右子树高
故可以定义平衡二叉树结点:
//平衡二叉树结点
typedef struct AVLNode{
int key; //数据域
int balance; //平衡因子
struct AVLNode *lchild, *rchild;
}AVLNode, *AVLTree;
调整最小不平衡子树
调整1(LL)
调整2(RR)
调整3(LR)
调整4(RL)
总结来看,就是调整最小不平衡子树,则其他的子树包括总的树都会平衡。
查找效率分析
平衡二叉树——树上任一结点的左子树和右子树的高度之差不超过1.
假设以 n h n_h nh表示深度为 h h h的平衡树中含有的最少结点数,
则有$n_0 = 0, n_1 = 2, $ 并且有 n h = n h − 1 + n h − 2 + 1 n_h = n_{h-1} + n_{h-2} + 1 nh=nh−1+nh−2+1.
所以含有 n n n个结点的平衡二叉树的最大深度为 O ( log 2 n ) O(\log_2n) O(log2n),平衡二叉树的平均查找长度为 O ( log 2 n ) O(\log_2n) O(log2n)。
哈夫曼树
带权路径长度
· 结点的权:有某种现实含义的数值(如:表示结点的重要性等)
· 结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积
· 树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length)
W P L = ∑ i = 1 n w i l i WPL = \sum_{i=1}^n{w_il_i} WPL=i=1∑nwili
哈夫曼树的定义(Huffman Tree)
在含有 n n n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树。
哈夫曼树的构造
给定 n n n个权值分别为 w 1 , w 2 , . . . , w n w_1, w_2,...,w_n w1,w2,...,wn的结点,构造哈夫曼树的算法描述如下:
- 将这 n n n个结点分别作为 n n n棵仅含一个结点的二叉树,构成森林 F F F;
- 构造一个新结点,从 F F F中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和;
- 从 F F F中删除刚才选出的两棵树,同时将新得到的树加入 F F F中;
- 重复步骤2和3,直至 F F F中剩下一棵树为止。