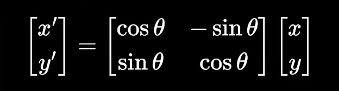【寻找佳慧】“第一关”——无所不能的矩阵（java实现代码）

作者简介：东星耀杨，C站煮播之星，【无规则教学】创始人，曾奉太上老君之名下凡，为了给迷途中的兄弟萌指点迷津，帮助兄弟萌早日踏入如我这般境界！世人见我，皆称之“王霸之气侧漏”的男人，哇靠蒸滴c！c了兄弟萌！

往期回顾：
_{【耀杨的罗曼史】小红：耀杨欧巴，能教教我hashmap吗？【雀氏润】}
耀杨和兄弟萌的约定：等我到一千粉，给兄弟萌发红包！感谢兄弟萌的陪伴和支持！
目录下面奉上本人靓照

兄弟萌兄弟萌~想你们啦！！！终于可以来陪兄弟萌啦，不得不说跟兄弟萌分开真的是一件难熬的事情，好啦，兄弟萌今天还是跟往常一样，认真教学，做一个安静的小男孩！！！
、
“百分百无规则教学时间！”

《为了遇见——迷失小键》

• 这个故事要追溯到很久很久之前……

• 三天之前我在港诡小道带着小键游山玩水，沿路的风景蒸滴很好，可能小键蒸滴很喜欢这样阴森森的风光，非拉着我过来，谁叫这是我unique的小键，我抓紧了小键的手，不管在这阴森境地遇上了什么，我都不会松手……要问为什么，因为我好怕怕！！！小键是个趁手的家伙。
  

• 话虽这么说，奈何我耀杨也是个凶猛的小男孩，肯定要在爱的人面前装装样子啦。也可能跟着喜欢的人，周遭的场景似乎也可爱起来了，一时间我竟然鼓起了小熊糖，一直“嗨害嗨”地给自己心理暗示。

• 可是终归好景不长，当我们走了一道门，突然之间电光火石，小键以我肉眼无法辨别的速度被一直手拉进了铁门，我愣住原地昏迷不醒……

• 醒来后，眼前闪烁着四个大字：“找到佳慧！！！”

《我耀杨不懂矩阵？》

在我们计算机江湖中一直流传着这样一句话：矩阵是无所不能的。我们在荧幕中所看到的二维三维图形的移动变换，放大缩小，任由我们的“摆布”，可是你知道这些变换是如何在计算机中实现的吗？在这一章耀杨带着兄弟萌初步了解这无所不能的矩阵，也为了破掉这层矩阵找到佳慧！！！

1.物体的坐标变换

咱们直接进入正题，计算机中我们锁看到的物体移动无疑例外设计到坐标变换，平移，旋转，缩放这些都伴随着坐标的变换。

计算机会根据物体在计算机中的位置以及我们的位置分别对物体的各个定点进行一系列的坐标运算，最后投影到屏幕上被我们所看到二维图像。

计算机中的图形不可能想现实中可以用“力”来实现，那么计算机是怎么移动这些物体的呢？这些坐标自然有了作用。

1.1平移：

x’=x+t_x
y’=y+t_y

由于在计算机中对物体进行顶点之间的操作过去繁琐，在对多物体操作的时候用矩阵的乘法进行运算不仅大大提高了效率，也方便了物体进行连续的变换。

加法转变成矩阵相乘比较有意思~由于加法中涉及到常量tx和ty所以无法直接通过2*2矩阵进行变换，在这里给兄弟萌讲解一个技巧——齐次坐标，这种给矩阵添加一个维度的技巧在矩阵运算中经常用到，还可以通过其次坐标进行矩阵的除法运算。

1.2缩放：

x’=Sx * x
y’=Sy * y

1.3旋转：

如图：可得出旋转后的坐标为：(通过正弦公式和余弦公式)

x’=xcosθ-ysinθ
y’=xsinθ+ycosθ

通过这个结果我们推导到矩阵计算是：

根据这样的定义，我们就可以推导二维空间中的任意变换都可以用一个3 * 3 矩阵来表示。

同理，在三维空间中的任意变换我们可以用一个4 * 4 矩阵来表示。

在4 * 4矩阵中还可以实现三维物体的透视投影，凭借齐次坐标实现矩阵的除法等等。

当然了关于矩阵还有很多更深入的知识等着大家探索，为师之后也会给大家持续教学！

1.4矩阵乘法

加减法为师就不介绍了，想必兄弟萌也都明白。

2.java实现矩阵的相关运算

2.1创建矩阵：

public int[][] createMatric(int row,int colum){
		@SuppressWarnings("resource")
		Scanner input=new Scanner(System.in);
		int array[][]=new int[row][colum];
		for(int i=0;i<array.length;i++)
			for(int j=0;j<array[i].length;j++){
				array[i][j]=input.nextInt();
			}
		return array;
	}

2.2矩阵加法：

public int[][] matricAdd(int matric1[][],int matric2[][] ){
		int matric3[][]=new int[matric1.length][matric1[0].length];
		if(matric1.length!=matric2.length||matric1[0].length!=matric2[0].length){			
			System.out.println("输入格式有误");
			System.exit(0);
		}else{
			for(int i=0;i<matric1.length;i++)
				for(int j=0;j<matric1[0].length;j++)
					matric3[i][j]=matric1[i][j]+matric2[i][j];
		}
		return matric3;
	}

2.3矩阵减法：

public int[][] matricJian(int matric1[][],int matric2[][] ){
		int matric3[][]=new int[matric1.length][matric1[0].length];
		if(matric1.length!=matric2.length||matric1[0].length!=matric2[0].length){
			System.out.println("输入格式有误");
			System.exit(0);
		}else{
			for(int i=0;i<matric1.length;i++)
				for(int j=0;j<matric1[0].length;j++){
					matric3[i][j]=matric1[i][j]-matric2[i][j];
				}
		}
		return matric3;
	}

2.4矩阵乘法：

public int[][] matricCheng(int matric1[][],int matric2[][]){
		int matric3[][]=new int[matric1.length][matric1[0].length];
		if(matric1.length!=matric2[0].length||matric1[0].length!=matric2.length){
			System.out.println("输入格式有误");
			System.exit(0);//退出虚拟机
		}else {
			for(int i=0;i<matric1.length;i++)
				for(int j=0;j<matric2[0].length;j++)
					for(int k=0;k<matric2.length;k++)
						matric3[i][j]+=matric1[i][k]*matric2[k][j];
		}
		return matric3;
	}

2.5矩阵的转置

public int[][] matricReserve(int matric[][]){
		int matric3[][]=new int[matric[0].length][matric.length];
		for(int i=0;i<matric.length;i++) {
			for(int j=0;j<matric[0].length;j++) {
				matric3[j][i]=matric[i][j];
			}
		}
		return matric3;
	}

2.6矩阵和数字相乘

public int[][] matricShuCheng(int matric[][],int x){
		for(int i=0;i<matric.length;i++)
			for(int j=0;j<matric[0].length;j++) {
				matric[i][j]=matric[i][j]*x;
			}
		return matric;
	}

2.7矩阵的输出

public void inputMatric(int matric[][]) {
		System.out.println("运算结果为:");
		for(int i=0;i<matric.length;i++) {
			for(int j=0;j<matric[0].length;j++) {
				System.out.print(matric[i][j]+" ");
			}
			System.out.println("");
		}
	}

《矩阵已破，心念小键》

兄弟萌今天又是努力教学的一天，为了我最最亲爱的兄弟萌！！！也为了我最最挚爱的小键！！！

今天晚上没有小键在身边，好不习惯兄弟萌，我只有你萌了……

说着说着眼泪就不争气地流下来了……

兄弟萌我先溜了，不知道佳慧什么时候还会布局，我耀杨是不会放弃的！！！