离散余弦变换滤波算法（DCT）

离散余弦变换滤波算法（DCT）

之前介绍的所有滤波算法都是空间域滤波算法（即2D滤波算法），今天来介绍一下频率域滤波算法，之后还会介绍时间域滤波算法（即3D滤波算法），敬请期待。

时间域相对于空间域增加了一个时间维度，可以对不同时间段的图像进行处理，对时域噪声有很好的抑制作用。而频率域又是一个全新的维度，换个角度看问题，将图像转换到频域，高频部分代表图像的细节、纹理信息，低频部分代表图像的轮廓信息，可以再特定的“频率”范围内对图像进行处理，就像是用显微镜看图像一样，能挖掘图像更加广阔的信息。

在图像处理中，图像为离散二维矩阵，所以算法都是离散形式。离散余弦变换是一种频率域转为到空间域的数学工具（函数），它为频率域与空间域架起一座桥梁。离散余弦变换是离散傅里叶变换（DFT）的一种特殊形式，特殊点就在于其原始变换信号是一个实偶函数。DCT变换较DFT变换具有更好的频域能量聚集度，那么对于那些不重要的频域区域和系数就能够直接裁剪掉，因此，DCT变换非常适合于图像压缩算法的处理，例如现在大名鼎鼎的jpeg就是使用了DCT作为图像压缩算法。

离散余弦变换，本质上是一种数学方法。它与傅立叶变换，小波变换，超小波变换，这些变换本质都是一种基变换，对于不同的系统，不同的研究对象，我们可以选取不同的基来让研究和分析变得更加简单。比如因为复指数信号是线性时不变系统的特征函数，因此我们在研究线性时不变系统及其特性时通常采用傅立叶变换，选取了一组好的基，可以让问题变得简单，比如我们的现在机器学习里很多的降维算法，像PCA，K-L变换也是基变换，对于一些基可能会出现很多很小的系数，或者是零系数，这要用这组基去表示这一信号或者向量时也就更加的简洁，而越是简洁就越于分析。

二维DCT变换公式如下：

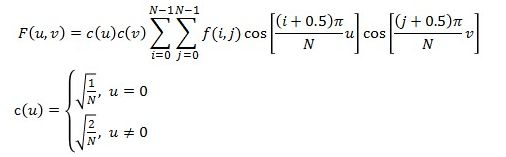
由公式我们可以看出，上面只讨论了二维图像数据为方阵的情况，在实际应用中，如果不是方阵的数据一般都是补齐之后再做变换的，重构之后可以去掉补齐的部分，得到原始的图像信息，这个尝试一下，应该比较容易理解
另外，由于DCT变换高度的对称性，在使用Matlab进行相关的运算时，我们可以使用更简单的矩阵处理方式：

DCT变换与IDCT变换，MATLAB代码实现：

clear;
clc;
% 正变换
X=round(rand(4)*100)   %产生随机矩阵
A=zeros(4);
for i=0:3
    for j=0:3
        if i==0
            a=sqrt(1/4);
         else
             a=sqrt(2/4);
         end            
         A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4);
    end
end

Y=A*X*A'        %DCT变换

%反变换
for i=0:3
    for j=0:3
         if i==0
             a=sqrt(1/4);
         else
             a=sqrt(2/4);
         end            
         A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4); %生成变换矩阵
     end
end

X1=A'*Y*A  %DCT反变换恢复的矩阵

% Matlab版
YY=dct2(X)      %Matlab自带的dct变换
XX=idct2(YY)    %Matlab自带的idct逆变换

因为噪声主要存在于高频信息中，对高频信息进行适当抑制，可以起到图像去噪的作用，这里采用简单高频抑制方法，可以降噪但也会丢失细节，中间处理的方法还有很多就不一一列举，MATLAB代码如下：

%读取图像
X=imread('lena.jpg'); 
X=rgb2gray(X);
%读取图像尺寸
[m,n]=size(X); 
%给图像加噪
Xnoised=imnoise(X,'gaussian',0.01); 
%输出加噪图像
subplot(121); 
imshow(Xnoised);
%DCT变换
Y=dct2(Xnoised); 
I=zeros(m,n);
%高频抑制
I(1:m/3,1:n/3)=1; 
Ydct=Y.*I;
%逆DCT变换
Y=uint8(idct2(Ydct)); 
%结果输出
subplot(122);
imshow(Y);

C++代码如下：

#include 
#include 
#include 
#include 
#include 


const int height = 128, width = 128, channel = 3;

// DCT hyper-parameter
int T = 8;
int K = 8;

// DCT coefficient
struct dct_str {
  double coef[height][width][channel];
};

// Discrete Cosine transformation
dct_str dct(cv::Mat img, dct_str dct_s){
  double I;
  double F;
  double Cu, Cv;

  for (int ys = 0; ys < height; ys += T){
    for (int xs = 0; xs < width; xs += T){
      for (int c = 0; c < channel; c++){
        for (int v = 0; v < T; v ++){
          for (int u = 0; u < T; u ++){
            F = 0;

            if (u == 0){
              Cu = 1. / sqrt(2);
            } else{
              Cu = 1;
            }

            if (v == 0){
              Cv = 1. / sqrt(2);
            }else {
              Cv = 1;
            }

            for (int y = 0; y < T; y++){
              for(int x = 0; x < T; x++){
                I = (double)img.at<cv::Vec3b>(ys + y, xs + x)[c];
                F += 2. / T * Cu * Cv * I * cos((2. * x + 1) * u * M_PI / 2. / T) * cos((2. * y + 1) * v * M_PI / 2. / T);
              }
            }

            dct_s.coef[ys + v][xs + u][c] = F;
          }
        }
      }
    }
  }

  return dct_s;
}

// Inverse Discrete Cosine transformation
cv::Mat idct(cv::Mat out, dct_str dct_s){
  double f;
  double Cu, Cv;

  for(int ys = 0; ys < height; ys += T){
    for(int xs = 0; xs < width; xs += T){
      for(int c = 0; c < channel; c++){
        for(int y = 0; y < T; y++){
          for(int x = 0; x < T; x++){
            f = 0;

            for (int v = 0; v < K; v++){
              for (int u = 0; u < K; u++){
                if (u == 0){
                  Cu = 1. / sqrt(2);
                } else {
                  Cu = 1;
                }

                if (v == 0){
                  Cv = 1. / sqrt(2);
                } else { 
                  Cv = 1;
                }

                f += 2. / T * Cu * Cv * dct_s.coef[ys + v][xs + u][c] * cos((2. * x + 1) * u * M_PI / 2. / T) * cos((2. * y + 1) * v * M_PI / 2. / T);
              }
            }

            f = fmin(fmax(f, 0), 255);
            out.at<cv::Vec3b>(ys + y, xs + x)[c] = (uchar)f;
          }
        }
      }
    }
  }

  return out;
}



// Main
int main(int argc, const char* argv[]){

  // read original image
  cv::Mat img = cv::imread("lena.jpg", cv::IMREAD_COLOR);

  // DCT coefficient
  dct_str dct_s;

  // output image
  cv::Mat out = cv::Mat::zeros(height, width, CV_8UC3);

  // DCT
  dct_s = dct(img, dct_s);

  // IDCT
  out = idct(out, dct_s);

  cv::imwrite("out.jpg", out);
  //cv::imshow("answer", out);
  //cv::waitKey(0);
  cv::destroyAllWindows();

Python代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# DCT hyoer-parameter 超参数
T = 8
K = 8
channel = 3

# DCT weight
def w(x, y, u, v):
    cu = 1.
    cv = 1.
    if u == 0:
        cu /= np.sqrt(2)
    if v == 0:
        cv /= np.sqrt(2)
    theta = np.pi / (2 * T)
    return (( 2 * cu * cv / T) * np.cos((2*x+1)*u*theta) * np.cos((2*y+1)*v*theta))

# DCT
def dct(img):
    H, W, _ = img.shape

    F = np.zeros((H, W, channel), dtype=np.float32)

    for c in range(channel):
        for yi in range(0, H, T):
            for xi in range(0, W, T):
                for v in range(T):
                    for u in range(T):
                        for y in range(T):
                            for x in range(T):
                                F[v+yi, u+xi, c] += img[y+yi, x+xi, c] * w(x,y,u,v)

    return F


# IDCT
def idct(F):
    H, W, _ = F.shape

    out = np.zeros((H, W, channel), dtype=np.float32)

    for c in range(channel):
        for yi in range(0, H, T):
            for xi in range(0, W, T):
                for y in range(T):
                    for x in range(T):
                        for v in range(K):
                            for u in range(K):
                                out[y+yi, x+xi, c] += F[v+yi, u+xi, c] * w(x,y,u,v)

    out = np.clip(out, 0, 255)
    out = np.round(out).astype(np.uint8)

    return out



# Read image
img = cv2.imread("imori.jpg").astype(np.float32)

# DCT
F = dct(img)

# IDCT
out = idct(F)

# Save result
cv2.imshow("result", out)
cv2.waitKey(0)
cv2.imwrite("out.jpg", out)