一阶导数和二阶导数的二阶/四阶中心差分格式
文章目录
- 一、问题提出
- 二、一阶导数和二阶导数的二阶中心差分格式
- 三、一阶导数和二阶导数的四阶中心差分格式
- 四、MATLAB代码
一、问题提出
已知一系列的数据点 ( x i , y i ) , i = 0 , 1 , 2 , . . . , n (x_i,y_i),i=0,1,2,...,n (xi,yi),i=0,1,2,...,n,且横坐标等间距(即 i ≥ 1 i\ge1 i≥1且 i ≤ n i\le n i≤n时,恒有 x i − x i − 1 = h x_i-x_{i-1}=h xi−xi−1=h),如何计算/估计一阶导数 f ′ ( x i ) f'(x_i) f′(xi)及二阶导数 f ′ ′ ( x i ) f''(x_i) f′′(xi)?
二、一阶导数和二阶导数的二阶中心差分格式
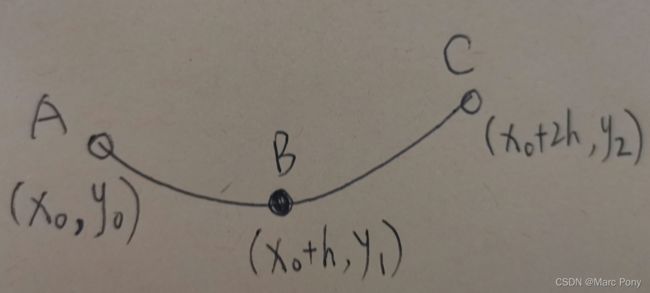
如上图,如何利用点B及其左右一个点的坐标(共三个点的坐标),来估计点B处一阶导数和二阶导数呢?想法非常简单:既然三个点的坐标已知,那么三个点可以插值得到一个一元二次多项式,求得一元二次多项式的系数后,就可以求多项式在B点处的一阶和二阶导数,从而得到一阶导数和二阶导数的二阶中心差分格式。利用matlab的符号计算可以很容易推导得到。
一阶导数的二阶中心差分格式:
f ′ ( x 0 + h ) = f ( x 0 + 2 h ) − f ( x 0 ) 2 h (1) f'(x_0+h)=\frac{f(x_0+2h)-f(x_0)}{2h} \tag 1 f′(x0+h)=2hf(x0+2h)−f(x0)(1)
二阶导数的二阶中心差分格式:
f ′ ′ ( x 0 + h ) = f ( x 0 ) − 2 f ( x 0 + h ) + f ( x 0 + 2 h ) h 2 (2) f''(x_0+h)=\frac{f(x_0)-2f(x_0+h)+f(x_0+2h)}{h^2} \tag 2 f′′(x0+h)=h2f(x0)−2f(x0+h)+f(x0+2h)(2)
三、一阶导数和二阶导数的四阶中心差分格式
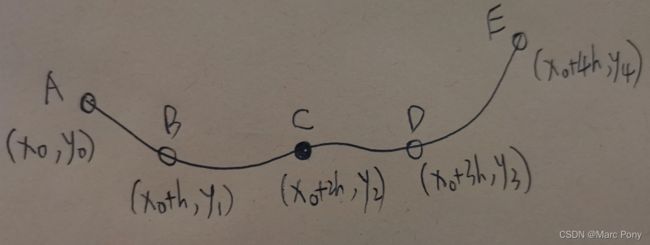
与一阶导数和二阶导数的二阶中心差分推导过程一样,一阶导数和二阶导数的四阶中心差分推导,只需将一元二次多项式插值改为一元四次多项式插值即可。
一阶导数的四阶中心差分格式:
f ′ ( x 0 + 2 h ) = f ( x 0 ) − 8 f ( x 0 + h ) + 8 f ( x 0 + 3 h ) − f ( x 0 + 4 h ) 12 h (3) f'(x_0+2h)=\frac{f(x_0)-8f(x_0+h)+8f(x_0+3h)-f(x_0+4h)}{12h} \tag 3 f′(x0+2h)=12hf(x0)−8f(x0+h)+8f(x0+3h)−f(x0+4h)(3)
二阶导数的四阶中心差分格式:
f ′ ′ ( x 0 + 2 h ) = − f ( x 0 ) − 16 f ( x 0 + h ) + 30 f ( x 0 + 2 h ) − 16 f ( x 0 + 3 h ) + f ( x 0 + 4 h ) 12 h 2 (4) f''(x_0+2h)=-\frac{f(x_0)-16f(x_0+h)+30f(x_0+2h)-16f(x_0+3h)+f(x_0+4h)}{12h^2} \tag 4 f′′(x0+2h)=−12h2f(x0)−16f(x0+h)+30f(x0+2h)−16f(x0+3h)+f(x0+4h)(4)
四、MATLAB代码
clc
clear
close all
syms x x0 y0 y1 y2 y3 y4 h real
%% 一阶导数和二阶导数的二阶中心差分格式
a = [1, x0, x0^2; 1, (x0 + h), (x0 + h)^2; 1, (x0 + 2 * h), (x0 + 2 * h)^2] \ [y0; y1; y2]; %一元二次多项式y(x) = a1 + a2 * x + a3 * x^2的系数
y(x) = a(1) + a(2) * x + a(3) * x^2;
dy(x) = diff(y, 1);
ddy(x) = diff(y, 2);
dy_two_order_central_difference = simplify(dy(x0 + h))
ddy_two_order_central_difference = simplify(ddy(x0 + h))
%% 一阶导数和二阶导数的四阶中心差分格式
a = [1, x0, x0^2, x0^3, x0^4; 1, (x0 + h), (x0 + h)^2, (x0 + h)^3, (x0 + h)^4; 1, (x0 + 2 * h), (x0 + 2 * h)^2, (x0 + 2 * h)^3, (x0 + 2 * h)^4; ...
1, (x0 + 3 * h), (x0 + 3 * h)^2, (x0 + 3 * h)^3, (x0 + 3 * h)^4; 1, (x0 + 4 * h), (x0 + 4 * h)^2, (x0 + 4 * h)^3, (x0 + 4 * h)^4] \ [y0; y1; y2; y3; y4]; %一元四次多项式y(x) = a1 + a2 * x + a3 * x^2 + a4 * x^3 + a5 * x^4的系数
y(x) = a(1) + a(2) * x + a(3) * x^2 + a(4) * x^3 + a(5) * x^4;
dy(x) = diff(y, 1);
ddy(x) = diff(y, 2);
dy_four_order_central_difference = simplify(dy(x0 + 2 * h))
ddy_four_order_central_difference = simplify(ddy(x0 + 2 * h))
%% 验证
n = 50;
x = linspace(0, 2*pi, n);
h = x(2) - x(1);
y = sin(x);
dy = cos(x);
ddy = -sin(x);
%一阶导数和二阶导数的二阶中心差分(第一个点和最后一个点无法估算一阶导数和二阶导数)
dy1 = nan * zeros(size(x));
ddy1 = nan * zeros(size(x));
for i = 2 : n - 1
dy1(i) = (y(i + 1) - y(i - 1)) / (2.0 * h);
ddy1(i) = (y(i - 1) - 2.0 * y(i) + y(i + 1)) / h^2;
end
%一阶导数和二阶导数的四阶中心差分(第一二个点和最后两个点无法估算一阶导数和二阶导数)
dy2 = nan * zeros(size(x));
ddy2 = nan * zeros(size(x));
for i = 3 : n - 2
dy2(i) = (y(i - 2) - 8.0 * y(i - 1) + 8.0 * y(i + 1) - y(i + 2)) / (12.0 * h);
ddy2(i) = -(y(i - 2) - 16.0 * y(i - 1) + 30.0 * y(i) - 16.0 * y(i + 1) + y(i + 2)) / (12.0 * h^2);
end
max_dy1_err = max(abs(dy1(2 : n - 1) - dy(2 : n - 1)));
max_ddy1_err = max(abs(ddy1(2 : n - 1) - ddy(2 : n - 1)));
max_dy2_err = max(abs(dy2(3 : n - 2) - dy(3 : n - 2)));
max_ddy2_err = max(abs(ddy2(3 : n - 2) - ddy(3 : n - 2)));
disp(['一阶导数的二阶和四阶中心差分近似,最大误差分别为:', num2str(max_dy1_err), ',' , num2str(max_dy2_err)])
disp(['二阶导数的二阶和四阶中心差分近似,最大误差分别为:', num2str(max_ddy1_err), ',' , num2str(max_ddy2_err)])
