深入浅出RSA算法
目录
公钥和私钥的产生:
加密消息:
解密消息:
数论基础:
算法优化:
确保万无一失
数字证书签发和验证流程
签发:
验证:
RSA算法是以数论为基础发展而来的,而数论——或者一些人称之为的算术,是最古老、最纯粹、最有活力、最初等却也是最深奥的数学领域。这门学科具有“数学皇后”的名声绝非偶然。一些最为复杂的传统的数学思想便是由对数论的基本问题的研究发展起来的。早在古希腊时代,人们就开始痴迷地研究数字,沉浸于这个几乎没有任何实用价值的思维游戏中。直到计算机诞生之后,几千年来的数论研究成果突然有了实际的应用,这个过程可以说是最为激动人心的数学话题之一。
RSA算法便是那个时代的产物,并且在密码学中拥有绝对的地位
原因很简单:
- 历史悠久: 1977 年,来自 MIT 的 Ron Rivest 、 Adi Shamir 和 Leonard Adleman 三个人合写了一篇论文,给出了一种至今仍然安全的公钥加密算法。随后,该算法以三人名字的首字母命名,即 RSA 算法。
- 原理简单: 基本上密码学都脱胎于数学,RSA算法虽然难以破解,但在数学上可以算得上十分简洁优美。它的原理十分简单:RSA 算法用到了一种非常犀利的不对称性——大数分解难题。对极大整数做因数分解的难度 (The Factoring Problem) 决定了 RSA 算法的可靠性。换言之,对一个极大整数做因数分解愈困难,RSA 算法就愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就肯定会极度下降。目前看来找到这样的算法的可能性非常小。
- 有效:RSA算法虽然很有历史,原理也十分简单,却经住了时间的考验,至今没有有效的攻击方式,属于ISO加密标准的一部分。
- 应用广泛: RSA算法是第一种既可以用于加密也可以用于签名的算法,简单的说就是既可以用来保护我的信息内容不被别人看见,又可以用来证明这个东西确实是我写的,不同场合都可以灵活使用。
所以说不管你从哪个方向入门密码学,RSA算法都是当之无愧的经典必学。
密码学不仅仅研究加密解密的数学算法。更多的时候,密码学研究保护信息安全的策略,我们可以称之为“协议”。在已有的数学模型基础上,我们往往忽略具体的数学实现方法,转而专注地研究借助这些数学工具能够构建的安全措施。
接下来来看RSA算法的具体实现过程
公钥和私钥的产生:
假设Alice 想通过一个不可靠的媒体接收 Bob 的一条私人讯息。她可以用以下的方式来产生一个公钥和一个私钥:
- 随意选择两个不同的大素数
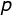 和
和 ,计算
,计算 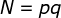
- 引用欧拉
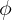 函数,小于N且与N互素的正整数个数
函数,小于N且与N互素的正整数个数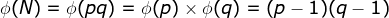
- 选择一个整数
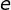 与
与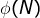 互素,并且
互素,并且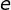 小于
小于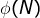
- 用以下这个公式计算(寻求)
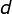 :
: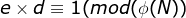 (
(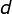 就是
就是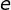 的模
的模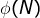 逆元,应用扩展欧几里德算法得到。)
逆元,应用扩展欧几里德算法得到。) - 将
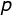 和
和 的记录销毀(当
的记录销毀(当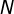 足够大时,寻找
足够大时,寻找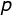 ,
, 将极其困难)
将极其困难) 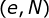 是公钥,
是公钥,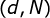 是私钥。
是私钥。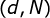 是秘密的。Alice将她的公钥,
是秘密的。Alice将她的公钥,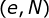 传给Bob,而将她的私钥
传给Bob,而将她的私钥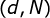 藏起来。
藏起来。
加密消息:
假设Bob 想给 Alice 送一个消息![]() ,他知道 Alice 产生的公钥
,他知道 Alice 产生的公钥![]() 。Bob使用事先与 Alice 约好的格式将
。Bob使用事先与 Alice 约好的格式将![]() 转换为一个小于
转换为一个小于![]() 的整数
的整数 ![]() ,比如他可以将每一个字符转换为其数宇形式的 Unicode 码,然后将这些数字连在一起组成整数
,比如他可以将每一个字符转换为其数宇形式的 Unicode 码,然后将这些数字连在一起组成整数![]() (假如他的信息非常长的话,他可以将这个信息分为几段,逐段加密)。公钥
(假如他的信息非常长的话,他可以将这个信息分为几段,逐段加密)。公钥![]() 应用下面的同余公式,将
应用下面的同余公式,将![]() 加密为
加密为![]() :
:
![]() 即
即 ![]()
Bob 算出C 后就可以将它经公开媒体传递给 Alice。
解密消息:
Alice 得到Bob 的消息![]() 后利用她的私钥
后利用她的私钥![]() 来解码。Alice 可以应用以下的同余公式将
来解码。Alice 可以应用以下的同余公式将![]() 转换为
转换为![]() :
:
![]() 即
即![]()
Alice 得到的![]() 就是Bob的
就是Bob的![]() ,因此可以将原来的信息
,因此可以将原来的信息![]() 准确复原。
准确复原。
看到这里是不是看懵了,没有系统学过数论的读者也许无法理解其背后的含义,这里先来介绍几个最基本的定理:
数论基础:
- 辗转相除法:欧几里得算法又称辗转相除法,是指用于计算两个a,b的最大公约数。应用领域有数学和计算机两个方面。计算公式
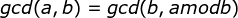
- 中国剩余定理::给出 m 个两两互质的整数,它们的乘积为 P ;假设有一个未知数 M ,如果我们已知 M 分别除以这 m 个数所得的余数,那么在 0 到 P – 1 的范围内,我们可以唯一地确定这个 M 。
- 扩展的辗转相除:即扩展欧几里得算法,考虑形如 a · x mod n = b的方程。寻找方程 a · x mod n = b 的解,相当于寻找一个 a 的倍数使得它除以 n 余 b ,或者说是寻找一个数 M 同时满足 M mod a = 0 且 M mod n = b 。如果 a 和 n 是互质的,那么根据中国剩余定理,这样的 M 一定存在,并且找到一个这样的 M 之后,在它的基础上加减 a · n 的整倍数,可以得到所有满足要求的 M 。求解方程的解的最基本的思路是不断的寻找a的某个倍数以及n的某个倍数,使得它们之间的差越来越小,直到最终变为 1 。在求解过程,我们相当于对a和 n做了一遍辗转相除:因而,算法的步骤数仍然是对数级别的,即使面对上百位上千位的大数,计算机也毫无压力。
- Fermat 小定理:如果 n 是一个质数的话,那么对于任意一个数 a , a 的 n 次方减去 a 之后都将是 n 的倍数。Fermat 小定理有一个等价的表述:如果 n 是一个质数的话,那么对于任意一个数 a ,随着 i 的增加, a 的 i 次方除以 n 的余数将会呈现出长度为 n – 1 的周期性。a的n次方与 a 的差能够被 n 整除,这说明a的n次方和 a 分别都除以 n 之后将会拥有相同的余数。
- Fermat – Euler 定理:在 1 到 n 的范围内有多少个数和 n 互质(包括 1 在内), a 的 i 次方除以 n 的余数序列就会有一个多长的周期。
- 对于任意两个数,两个数的乘积一定是它们的一个公倍数,但若这两个数互质,则它们的乘积一定是它们的最小公倍数。
- a 和 b 的最大公约数和最小公倍数的乘积,一定等于 a 和 b 的乘积。(6,7其实可以算为一条)
- 1). (a+b) % c = ((a%c) + (b%c))%c
2). (a-b) % c = ((a%c) - (b%c))%c
3). (a×b) % c = ((a%c) × (b%c))%c
现在回头再看一遍是不是清晰很多了,但是以上的均是结论,没有给出证明,读者如果想要了解的话,可以拿任意一本初等数论的书进行精读。
我们现在只记住上面的结论,来看给有意思的问题“如何简化RSA算法的时间复杂度?”
算法优化:
现实中, ![]() 和
和 ![]() 都是上百位的大数,老老实实的去做乘法,内存迟早要崩溃。怎么办呢?别忘了,“反正最后都要对乘积取余,相乘之前事先对乘数取余不会对结果造成影响”,因此我们可以在运算过程中边算边取余,每做一次乘法都只取乘积除以
都是上百位的大数,老老实实的去做乘法,内存迟早要崩溃。怎么办呢?别忘了,“反正最后都要对乘积取余,相乘之前事先对乘数取余不会对结果造成影响”,因此我们可以在运算过程中边算边取余,每做一次乘法都只取乘积除以 ![]() 的余数。这样一来,我们的每次乘法都是两个
的余数。这样一来,我们的每次乘法都是两个 ![]() 以内的数相乘了。而
以内的数相乘了。而 ![]() 是两个质数
是两个质数 ![]() 和
和 ![]() 的乘积。由于
的乘积。由于 ![]() 和
和 ![]() 都是质数,它们显然也就互质了。因而,如果我们知道
都是质数,它们显然也就互质了。因而,如果我们知道![]() 分别除以
分别除以 ![]() 和
和 ![]() 的余数,也就能够反推出它除以
的余数,也就能够反推出它除以 ![]() 的余数了。因此,在反复平方的过程中,我们只需要保留所得的结果除以
的余数了。因此,在反复平方的过程中,我们只需要保留所得的结果除以 ![]() 的余数和除以
的余数和除以 ![]() 的余数即可,运算时的数字规模进一步降低到了
的余数即可,运算时的数字规模进一步降低到了 ![]() 和
和 ![]() 所在的数量级上。更神的是,别忘了,
所在的数量级上。更神的是,别忘了, ![]() 除以
除以 ![]() 的余数是以
的余数是以![]() 为周期的,同理
为周期的,同理![]() 处以
处以![]() 的余数也是以
的余数也是以![]() 为周期的。由于余数的周期性现象,计算
为周期的。由于余数的周期性现象,计算![]() 就相当于计算
就相当于计算 ![]() 。这样一来,连指数的数量级也减小到了和
。这样一来,连指数的数量级也减小到了和 ![]() 、
、 ![]() 相同的水平, RSA 运算的速度会有明显的提升。
相同的水平, RSA 运算的速度会有明显的提升。
确保万无一失
上述方案让双方在不安全的通信线路上神奇地约定好了密码,一切看上去似乎都很完美了。然而,在这个漂亮的解决方案背后,有一个让人意想不到的、颇有些喜剧色彩的漏洞——中间人攻击。在 A 、 B 两人建立会话的过程中,攻击者很容易在线路中间操纵信息,让 A 、 B 两人误以为他们是在直接对话。让我们来看看这具体是如何操作的吧。建立会话时, A 首先呼叫 B 并索要 B 的公钥,此时攻击者注意到了这个消息。当 B 将公钥回传给 A 时,攻击者截获 B 的公钥,然后把他自己的公钥传给 A 。接下来, A 随便想一个密码,然后用他所收到的公钥进行加密,并将加密后的结果传给 B 。 A 以为自己加密时用的是 B 的公钥,但他其实用的是攻击者的公钥。攻击者截获 A 传出来的信息,用自己的私钥解出密码,再把密码用 B 的公钥加密后传给 B 。 B 收到信息后不会发现什么异样,因为这段信息确实能用 B 的私钥解开,而且确实能解出正确的信息。今后, A 、 B 将会用密码进行通话,而完全不知道有攻击者已经掌握了密码。
怎么封住这个漏洞呢?我们得想办法建立一个获取对方公钥的可信渠道。一个简单而有效的办法就是,建立一个所有人都信任的权威机构,由该权威机构来储存并分发大家的公钥。这就是我们通常所说的数字证书认证机构,英文是 Certificate Authority ,通常简称 CA 。任何人都可以申请把自己的公钥放到 CA 上去,不过 CA 必须亲自检查申请者是否符合资格。如果 A 想要和 B 建立会话,那么 A 就直接从 CA 处获取 B 的公钥,这样就不用担心得到的是假的公钥了。
客户端拿到了服务端的数字证书后,要怎么校验该数字证书是真实有效的呢?
在说校验数字证书是否可信的过程前,我们先来看看数字证书是什么,一个数字证书通常包含了:
- 公钥;
- 持有者信息;
- 证书认证机构(CA)的信息;
- CA 对这份文件的数字签名及使用的算法;
- 证书有效期;
- 还有一些其他额外信息;
数字证书签发和验证流程
签发:
- 首先 CA 会把持有者的公钥、用途、颁发者、有效时间等信息打成一个包,然后对这些信息进行 Hash 计算,得到一个 Hash 值;
- 然后 CA 会使用自己的私钥将该 Hash 值加密,生成 Certificate Signature,也就是 CA 对证书做了签名;
- 最后将 Certificate Signature 添加在文件证书上,形成数字证书;
验证:
- 首先客户端会使用同样的 Hash 算法获取该证书的 Hash 值 H1;
- 通常浏览器和操作系统中集成了 CA 的公钥信息,浏览器收到证书后可以使用 CA 的公钥解密 Certificate Signature 内容,得到一个 Hash 值 H2 ;(把加密钥匙和解密钥匙称作“公钥”和“私钥”是有原因的——有时候,私钥也可以用来加密,公钥也可以用来解密。)
- 最后比较 H1 和 H2,如果值相同,则为可信赖的证书,否则则认为证书不可信。
至此为止,建立安全的通信线路终于算是有了一个比较完美的方案。在我们日常上网中,也许在不知不觉中就进行了几次RSA算法验证,最经典的例子就是HTTPS基于RSA算法的T LS握手,可见,它直到今天也仍然绽放着光彩。