SEAL学习第一天: bfv_basics使用用法
SEAL学习第一天: bfv_basics使用用法
目录
- SEAL学习第一天: bfv_basics使用用法
- bfv_basics
-
- 一 parms类
-
- size_t poly_modulus_degree
- coeff_modulus
- MOD
-
- 演示code
- 二 KeyGenerator类
-
-
- 演示code
-
- 线性化 Relinearization
-
-
- 演示Code
-
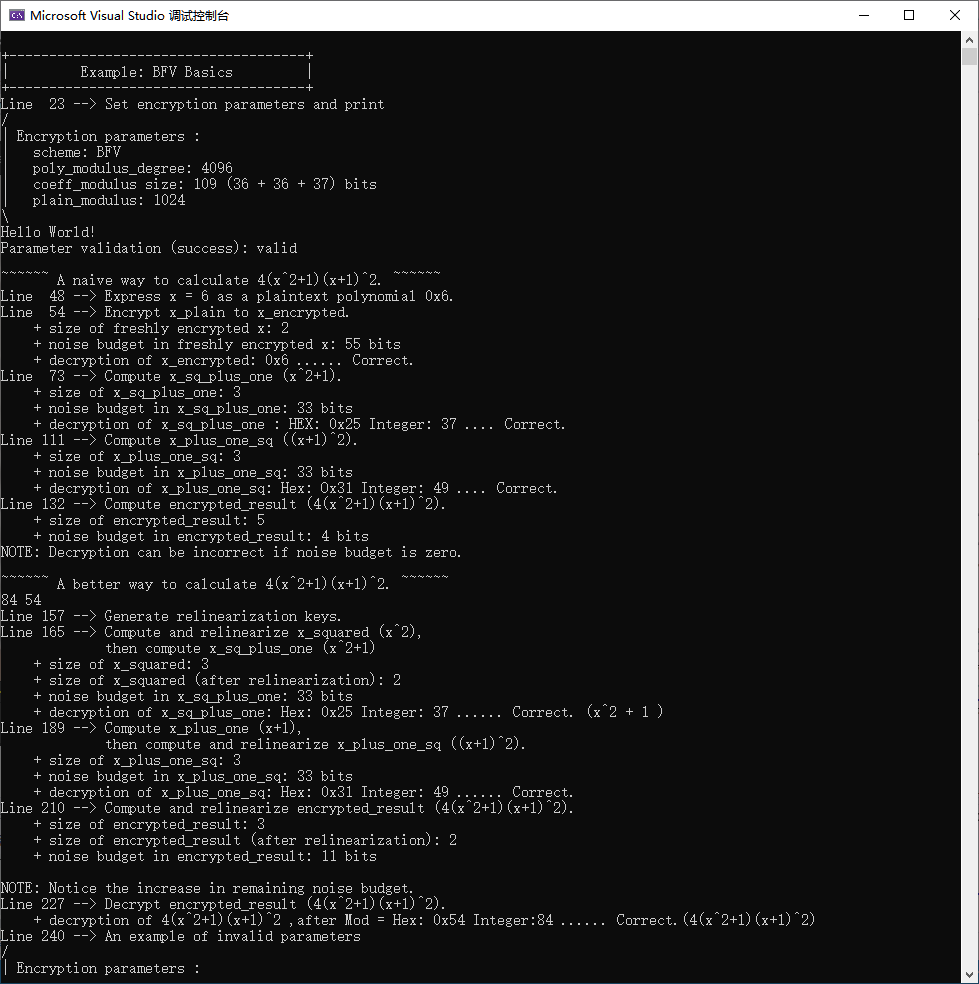
- 源代码
bfv_basics
一 parms类
创建一个HE方案类
parms类需要的3个参数
- poly_modulus_degree (degree of polynomial modulus 多项式模的次数);
- coeff_modulus ([ciphertext] coefficient modulus 系数模);
- plain_modulus (plaintext modulus; only for the BFV scheme). MOD X, 将结果MOD到X内
| 用法 | 参数 | 解释说明 |
|---|---|---|
| EncryptionParameters parms(); | scheme_type::bfv | 创建一个HE以BFV方案类 |
| size_t poly_modulus_degree = 4096; | integear | [size_t poly_modulus_degree](###size_t poly_modulus_degree) |
| parms.set_poly_modulus_degree(); | poly_modulus_degree | |
| parms.set_coeff_modulus(); | CoeffModulus::BFVDefault(poly_modulus_degree) | poly_modulus_degree |
| parms.set_plain_modulus(1024); | integear | MOD |
| context.parameter_error_message() | 输出报错信息 | |
| SEALContext context(parms); | 创建SEALContext类 |
EncryptionParameters parms(scheme_type::bfv);
The BFV scheme cannot perform arbitrary computations on encrypted data.
Instead, each ciphertext has a specific quantity called the `invariant noise
budget' -- or `noise budget' for short -- measured in bits. The noise budget
in a freshly encrypted ciphertext (initial noise budget) is determined by
the encryption parameters. Homomorphic operations consume the noise budget
at a rate also determined by the encryption parameters. In BFV the two basic
operations allowed on encrypted data are additions and multiplications, of
which additions can generally be thought of as being nearly free in terms of
noise budget consumption compared to multiplications. Since noise budget
consumption compounds in sequential multiplications, the most significant
factor in choosing appropriate encryption parameters is the multiplicative
depth of the arithmetic circuit that the user wants to evaluate on encrypted
data. Once the noise budget of a ciphertext reaches zero it becomes too
corrupted to be decrypted. Thus, it is essential to choose the parameters to
be large enough to support the desired computation; otherwise the result is
impossible to make sense of even with the secret key.
基本运算: 加法 和乘法
In BFV the two basic operations allowed on encrypted data are additions and multiplications
基本运算: 加法 和乘法
size_t poly_modulus_degree = 4096;
size_t poly_modulus_degree
多项式模”的次数,2的倍数;1024, 2048, 4096, 8192, 16384, 32768,
parms.set_poly_modulus_degree(poly_modulus_degree);
parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree));
coeff_modulus
[ciphertext] `coefficient modulus' (coeff_modulus) [密文]'系数模量' (coeff_modulus)
Microsoft SEAL comes with helper functions for selecting the coeff_modulus.
For new users the easiest way is to simply use
简单调用:
CoeffModulus::BFVDefault(poly_modulus_degree),
返回vector类型
which returns std::vector consisting of a generally good choice
for the given poly_modulus_degree.
模长度对应素数长度
+----------------------------------------------------+
| poly_modulus_degree | max coeff_modulus bit-length |
+---------------------+------------------------------+
| 1024 | 27 |
| 2048 | 54 |
| 4096 | 109 |
| 8192 | 218 |
| 16384 | 438 |
| 32768 | 881 |
+---------------------+------------------------------+
parms.set_plain_modulus(1024);
MOD
~ log2(coeff_modulus/plain_modulus) (bits)
噪声预算计算方式:
and the noise budget consumption in a homomorphic multiplication is of the
form log2(plain_modulus) + (other terms).
明文模量是BFV格式特有的,使用CKKS格式时不能设置明文模量。
既然所有参数都设置好了,我们就可以构建一个SEALContext了
对象。类的有效性和属性是一个重类 我们刚刚设置的参数。
演示code
EncryptionParameters parms(scheme_type::bfv); //声明HE 使用的模式
// 设置 3 个参数
size_t poly_modulus_degree = 4096;
parms.set_poly_modulus_degree(poly_modulus_degree);
parms.set_coeff_modulus(CoeffModulus::BFVDefault(poly_modulus_degree));
parms.set_plain_modulus(1024); // 明文 MOD数 (2的倍数, 素数最好)
//创建一个context
SEALContext context(parms);
//当使用参数创建SEALContext时,Microsoft SEAL将首先创建验证这些参数。这里选择的参数是有效的。
cout << "Parameter validation (success): " << context.parameter_error_message() << endl;
二 KeyGenerator类
公钥加密方案有一个用于加密数据的单独的公钥,和一个用于解密数据的单独的秘密密钥。
我们需要KeyGenerator类的一个实例。构造密钥生成器会自动生成一个密钥。然后,我们可以使用
KeyGenerator::create_public_key为它创建尽可能多的公钥。
| 用法 | 参数 | 解释说明 |
|---|---|---|
| KeyGenerator keygen(context); | SEALContext | 创建一个钥匙生成器 |
| SecretKey secret_key = keygen.secret_key(); | 创造一个私钥 | |
| PublicKey public_key; | 声明一个公钥 | |
| keygen.create_public_key(public_key); | 创造一个公钥 | |
| Encryptor encryptor(); | SEALContext,PublicKey | 构造Encryptor的一个实例 |
| Evaluator evaluator(); | SEALContext | 对密文的计算使用Evaluator类执行 |
| Decryptor decryptor(); | SEALContext,SecretKey | 构造Decryptor类的一个实例 |
Note that KeyGenerator::create_public_key has another overload that takes
no parameters and returns a Serializable object. We will discuss
this in `6_serialization.cpp'.
为了能够加密,我们需要构造Encryptor的一个实例,注意,加密器只需要公钥,
Encryptor encryptor(contest,public_key);
对密文的计算使用Evaluator类执行,Evaluator不会由持有密钥的同一方构造。
Evaluator evaluator(context);
当然,我们希望对结果进行解密,以验证一切工作正常,因此还需要构造Decryptor类的一个实例。注意,解密器需要密钥。
Decryptor decryptor(context, secret_key);
演示code
Ciphertext x_encrypted; // 密文
encryptor.encrypt(x_plain, x_encrypted); // 将明文 x_plain 加密输出到密文x_encrypted上
Plaintext x_decrypted;
decryptor.decrypt(x_encrypted, x_decrypted); // 解密 将加密密文,输出覆盖到明文上
cout << "Compute x_sq_plus_one (x^2+1)." << endl;
Ciphertext x_sq_plus_one;
evaluator.square(x_encrypted, x_sq_plus_one); // 计算平方, 结果输出到 x_sq_plus_one 中
Plaintext plain_one("1"); // 明文 1
/**
加密的乘法导致输出密文的大小增加。
更准确地说,如果输入密文的大小为M和N,则输出
同态乘法后的密文大小为M+N-1。
**/
线性化 Relinearization
`Relinearization’ is an operation that reduces the size of a ciphertext after
multiplication back to the initial size, 2. Thus, relinearizing one or both
input ciphertexts before the next multiplication can have a huge positive
impact on both noise growth and performance, even though relinearization has
a significant computational cost itself. It is only possible to relinearize
size 3 ciphertexts down to size 2, so often the user would want to relinearize
after each multiplication to keep the ciphertext sizes at 2.Relinearization requires special `relinearization keys’, which can be thought
of as a kind of public key. Relinearization keys can easily be created with
the KeyGenerator.
“重新线性化”是一种减少密文大小的操作。
乘法返回初始大小2。因此,重新线性化一个或两个
下一个乘法之前的输入密文可以具有很大的正数
即使重新线性化已对噪声增长和性能产生影响
巨大的计算成本本身。 只能重新线性化
大小为3的密文,大小减小为2,因此用户经常需要重新线性化
每次乘法后,将密文大小保持为2。重新线性化需要特殊的“重新线性化键”,可以认为
作为一种公钥。 重新线性化键可以轻松创建
KeyGenerator。
线性化用法
| 用法 | 参数 | 解释说明 |
|---|---|---|
| RelinKeys relin_keys; | 声明线性化类 | |
| keygen.create_relin_keys(relin_keys); | (RelinKeys) | 创建一个线性密钥 |
| evaluator.relinearize_inplace(x_squared, relin_keys); | (Ciphertext,RelinKeys) | 将计算结果重新线性化大小到2以内 |
演示Code
print_line(__LINE__);
cout << "Compute and relinearize x_squared (x^2)," << endl;
cout << string(13, ' ') << "then compute x_sq_plus_one (x^2+1)" << endl;
Ciphertext x_squared;
evaluator.square(x_encrypted, x_squared);
cout << " + size of x_squared: " << x_squared.size() << endl;
evaluator.relinearize_inplace(x_squared, relin_keys);// 重新线性化大小到2以内
cout << " + size of x_squared (after relinearization): " << x_squared.size() << endl;
evaluator.add_plain(x_squared, plain_one, x_sq_plus_one); // x_sq_plus_one = x_squared + plain_one;
cout << " + noise budget in x_sq_plus_one: " << decryptor.invariant_noise_budget(x_sq_plus_one) << " bits"
<< endl;
cout << " + decryption of x_sq_plus_one: ";
decryptor.decrypt(x_sq_plus_one, decrypted_result);
ss2.clear();
ss2 << hex << decrypted_result.to_string();
ss2 >> d2;
cout << "Hex: 0x" << decrypted_result.to_string() << " Integer: "<<d2<<" ...... Correct. (x^2 + 1 ) " << endl;
源代码
#include "seal/seal.h"
#include "examples.h"
#include