傅里叶变换
傅里叶变换
正向变换
F ( ω ) = ∫ − ∞ ∞ f ( x ) e − 2 π i ω x d x F(\omega)=\int_{-\infty}^{\infty} f(x) e^{-2 \pi i \omega x} d x F(ω)=∫−∞∞f(x)e−2πiωxdx
傅里叶逆变换
f ( x ) = ∫ − ∞ ∞ F ( ω ) e 2 π i ω x d ω f(x)=\int_{-\infty}^{\infty} F(\omega) e^{2 \pi i \omega x} d \omega f(x)=∫−∞∞F(ω)e2πiωxdω
e i x = cos x + i sin x e^{i x}=\cos x+i \sin x eix=cosx+isinx
一个很好的傅里叶变换教程视频:【官方双语】形象展示傅里叶变换
形象展示傅里叶变换
首先,这里有一个每秒3拍的音频的图像,十分简单也十分规律。

把这个图像缠绕在一个圆上

想象一个转动的变量,它的长度时刻等于图像的高度。
并且,本向量每过2s就转动一圈。
即为:向量的角速度为 π / s π/s π/s
本角速度可以随意指定,随着你指定角速度的变化,生成的图像也会随之变化,缠绕的频率(角速度)决定了缠绕图像的样子。
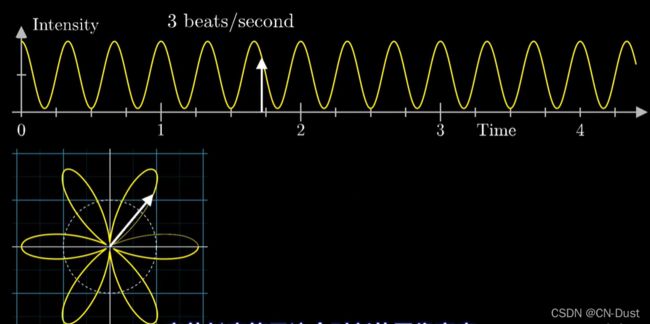
当缠绕频率和信号频率相等时(每秒3拍),就会出现以下特别的情况。所有搞点恰好落在圆的右侧,所有低点恰好落在圆的左侧。
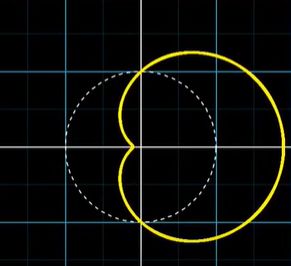
要利用好这一结论,我们可以把图像看成一个有质量的东西,比如金属丝。

不断改变缠绕频率,取其质心,观察其变化。当图像杂乱无章时,质心一直处于中心点附近。
但是,当缠绕频率和信号频率相等时,所有的峰落在右边,所有的谷落在左边,所以质心就会异常偏向右侧。

为了刻画这一现象,我们画一个图,记录缠绕频率对应质心的位置。
质心的位置是二维的,需要2个坐标来完整描述,但我们暂时只记录它的横坐标。
频率为0时,所有的点都落在右边,质心的横坐标相对较大。这里质心横坐标较大只需要理解其是因为频率为0导致的即可。

增加缠绕频率,质心的横坐标也就越趋向于0,此后,它会在0附近上下摆动。

但是,当当缠绕频率和信号频率相等时,也就是每秒3拍时,质心的横坐标会出现一个高峰,因为图像全部缠绕在右边。

当 2 H z + 3 H z 2Hz+3Hz 2Hz+3Hz的图像混在一起时,观察其质心变化。

不难发现,对于单纯的频率转换,除了在其频率时会出现一个尖峰以外,其余地方几乎都是0,通过本方法我们可以将 2 H z + 3 H z 2Hz+3Hz 2Hz+3Hz的图像分离成 2 H z 2Hz 2Hz图像+ 3 H z 3Hz 3Hz图像。
但是,以上介绍的全部是近傅里叶变换,真正的傅里叶变换需要将上方只考虑x坐标的情况,改变为质心在复平面上的情况。
用 e ( 2 π i f t ) e^(2πift) e(2πift)来表示。其中如果 f = 1 / 10 f=1/10 f=1/10,那么这个单位向量就是10s转一整圈。
改变其转动方向,则加个负号即可:
− e ( 2 π i f t ) -e^(2πift) −e(2πift)
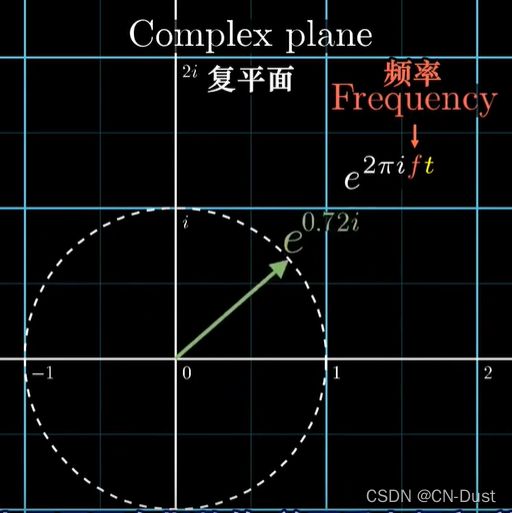
对于一个(描述信号强度与时间关系的)函数 g ( t ) g(t) g(t),将这个指数函数乘上 g ( t ) g(t) g(t),意思就是这个旋转的复数依照函数大小值被缩放了。这样就能将这个长度不断变化的旋转向量看作是在画出缠绕起来的图像了。
g ( t ) e − 2 π i f t g(t) e^{-2 \pi i f t} g(t)e−2πift
在函数上等间隔地取点,对应到图上的位置。
对函数做积分,再除以时间区间的长度。
1 t 2 − t 1 ∫ t 1 t 2 g ( t ) e − 2 π i f t d t \frac{1}{t_{2}-t_{1}} \int_{t_{1}}^{t_{2}}g(t)e^{-2 \pi i f t} d t t2−t11∫t1t2g(t)e−2πiftdt
而真傅里叶变换,只取其积分部分。
其含义不再是质心,而是把它倍增,如果原图像持续了3s,就把质心乘上3。
如果一个频率持续了很长时间,这个频率的傅里叶变换模长就被放的很大。

周期函数的傅里叶级数展开
周期函数
周期函数表达式为:
f ( x ) = f ( x + k T ) ( k = 1 , 2 , 3 … ) f(x) = f(x + kT) (k = 1,2,3…) f(x)=f(x+kT)(k=1,2,3…)
如果该周期函数满足狄利赫里条件,那么该周期可以展开为傅里叶级数:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a 0 cos ( n ω 1 t ) + b n sin ( n ω 1 t ) ) f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{0} \cos \left(n \omega_{1} t\right)+b_{n} \sin \left(n \omega_{1} t\right)\right) f(t)=2a0+n=1∑∞(a0cos(nω1t)+bnsin(nω1t))
其中傅里叶系数计算如下:
a 0 2 = 1 T ∫ t 0 t 0 + T f ( t ) d t a n = 2 T ∫ t 0 t 0 + T f ( t ) cos n ω 1 t d t b n = 2 T ∫ t 0 t 0 + T sin n ω 1 t d t \begin{gathered} \frac{a_{0}}{2}=\frac{1}{T} \int_{t_{0}}^{t_{0}+T} f(t) d t \\ a_{n}=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \cos n \omega_{1} t d t \\ b_{n}=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} \sin n \omega_{1} t d t \end{gathered} 2a0=T1∫t0t0+Tf(t)dtan=T2∫t0t0+Tf(t)cosnω1tdtbn=T2∫t0t0+Tsinnω1tdt

