12.2 Kruskal算法
文章目录
- 算法原理
- Python代码
- 本文案例测试代码
算法原理
Prim算法是从一个个点开始构建一棵树,但是Kruskal不是这样。Kruskal算法是在一开始时,将所有的点都视为独立的树,整个图视为森林。然后将树两两合并,合并时找权重最小的边,最终合并为一棵树。在合并后,将树加入到并查集中,通过并查集判断是否已经合过,也就是说通过并查集判断两个点是否已经连起来了。如果对并查集不熟悉,可以看我的博文6.7 并查集。我举个例子,以下是无向加权图:
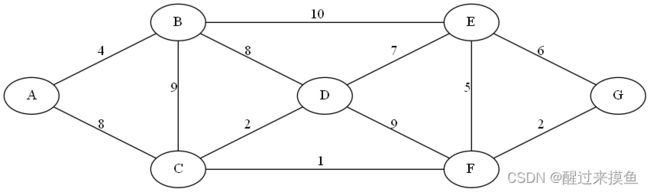
此时权重最小的边,是CF,直接连起来:
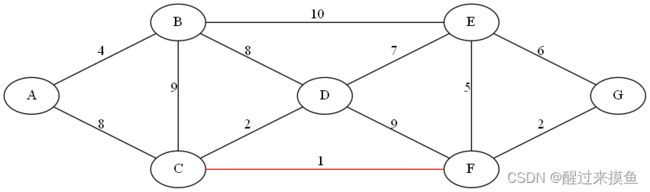
接下来最小的边是CD,由于并查集发现D和C不在同一个集合,表示CD不相连,那么连起来:
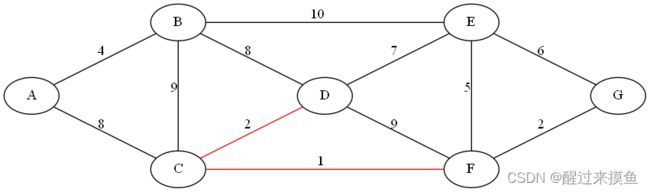
接下来是FG,不在同一个并查集,连起来:
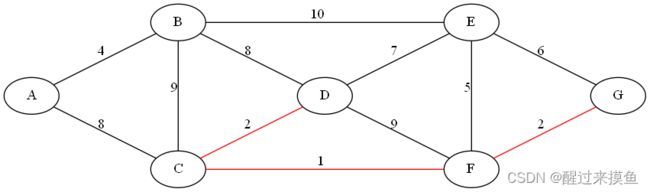
再接下里,最短的就是AB了,这两个也不在同一个并查集内,连起来:
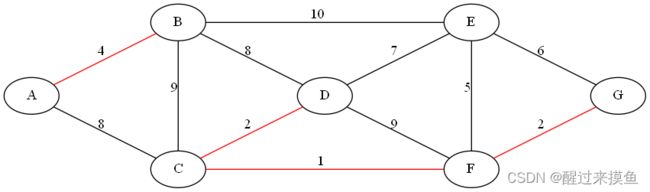
然后是EF,也不在同一并查集,连起来:
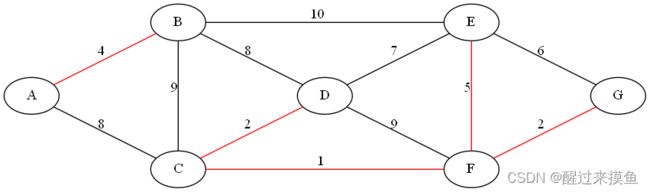
接下来的是AC,也不再同一并查集:
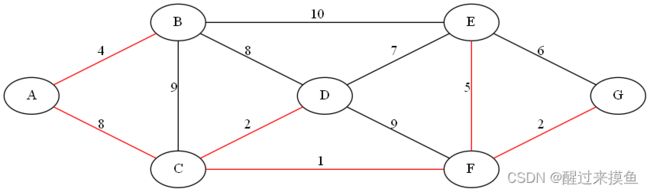
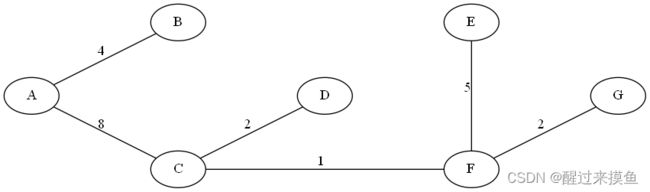
此时,不需要再去用并查集检查了,因为可以用一个计数器计算增加的边数,因为树有个特性,边的数量等于点的数量减去1。这个时候直接结束循环返回就可以了,最终的最小生成树如下:
Python代码
# _*_ coding:utf-8
import functools
class Edge:
def __init__(self, to, weight):
self.__to = to
self.__weight = weight
@property
def to(self):
return self.__to
@property
def weight(self):
return self.__weight
# 并查集
class Handler:
def __init__(self, vertex):
self.__vertex = vertex
self.__parent = self
self.__rank = 0
@property
def vertex(self):
return self.__vertex
@property
def parent(self):
return self.__parent
@parent.setter
def parent(self, value):
self.__parent = value
@property
def rank(self):
return self.__rank
@rank.setter
def rank(self, value):
self.__rank = value
def union(self, other):
if self.__rank > other.__rank:
other.__parent = self
else:
self.__parent = other
if self.__rank == other.__rank:
other.__rank = other.__rank + 1
def find(self):
x = self
if x != x.__parent:
x.__parent = x.parent.find()
return x.__parent
class DisjointSet:
# 对于每一个item,应该找到属于它的最小的集合
def __init__(self, n):
self.__forest = [None] * n
def make_set(self, item):
h = Handler(item)
self.__forest[item] = h
return h
def union_set(self, x, y):
self.find_set(x).union(self.find_set(y))
def find_set(self, item):
return self.__forest[item].find()
# wu
class WeightedGraph:
def __init__(self, vertices, edges, pos):
self.__vertices = vertices
self.__edges = edges
#用于图形化
self.__pos = pos
@property
def vertices(self):
return self.__vertices
@property
def edges(self):
return self.__edges
def kruskal(self):
#
a = [[] for _ in self.__vertices]
all_edges = []
for i, edges in enumerate(self.__edges):
for edge in edges:
all_edges.append((i, edge))
all_edges.sort(key = functools.cmp_to_key(lambda x,y:x[1].weight-y[1].weight))
n = len(self.__vertices)
s = DisjointSet(n)
for i in range(n):
s.make_set(i)
count = 1
for i, (u, edge) in enumerate(all_edges):
v = edge.to
# 因为是双向图,所以可以忽略掉一部分
if u > v:
continue
if s.find_set(u) != s.find_set(v):
a[u].append(edge)
a[v].append(Edge(u, edge.weight))
s.union_set(u, v)
print(f"添加完{i}", self.to_kruskal_dot( a))
count += 1
if count == n:
break
return a
def to_dot(self):
dot_s = 'graph s {\n\tlayout=fdp\n'
for i, v in enumerate(self.__vertices):
dot_s += f'\t"{v}"[pos="{self.__pos[i]}"];\n'
for i, e in enumerate(self.__edges):
for t in e:
if t.to < i:
continue
dot_s += f'\t\"{self.__vertices[i]}\"--"{self.__vertices[t.to]}"[label="{t.weight}"];\n'
dot_s += '}\n'
return dot_s
def to_kruskal_dot(self, a):
dot_s = 'graph s {\n\tlayout=fdp\n'
for i, v in enumerate(self.__vertices):
dot_s += f'\t"{v}"[pos="{self.__pos[i]}";'
dot_s += '];\n'
for i, e in enumerate(self.__edges):
for t in e:
if t.to < i:
continue
dot_s += f'\t\"{self.__vertices[i]}\"--"{self.__vertices[t.to]}"[label="{t.weight}";'
for st_edge in a[i]:
if st_edge.to == t.to:
dot_s += 'color=red;'
dot_s += '];\n'
dot_s += '}\n'
return dot_s
本文案例测试代码
import unittest
from com.youngthing.graph.kruskal import Edge
from com.youngthing.graph.kruskal import WeightedGraph
class PrimMstTestCase(unittest.TestCase):
def test_prim(self):
# 做一张图
vertices = [ 'A', 'B', 'C', 'D', 'E', 'F', 'G',]
# 设计容量
edges = [
[Edge(1, 4), Edge(2, 8), ],#a
[Edge(0, 4), Edge(2, 9), Edge(3, 8), Edge(4, 10)],#B
[Edge(0, 8), Edge(1, 9), Edge(3, 2), Edge(5, 1)],#C
[Edge(1, 8), Edge(2, 2), Edge(4, 7), Edge(5, 9)],#D
[Edge(1, 10), Edge(3, 7), Edge(5, 5), Edge(6, 6)],#E
[Edge(2, 1), Edge(3, 9), Edge(4, 5), Edge(6, 2)],#f
[Edge(4, 6), Edge(5, 2)],#g
]
pos = ["0,0!", "2,1!", "2,-1!", "4,0!", "6,1!", "6,-1!", "8,0!", ]
fn = WeightedGraph(vertices, edges, pos)
print(fn.to_dot())
tree = fn.kruskal()
print(WeightedGraph(vertices, tree, pos).to_dot())
if __name__ == '__main__':
unittest.main()