数据结构基础
数据结构基础
数据结构是一种数据组织,管理和存储的格式,它可以帮助我们实现对数据高效的访问和修改,数据结构也就是数据值的集合,可以体现数据之间的关系,以及可以对数据进行应用的函数或操作.
线性表
线性表是最基本的一种数据结构,它是表示一组相同类型数据的优先序列,你可以把它与数组进行参考,但是它并不是数组,线性表是一种表结构,它能够支持数据的插入、删除、更新、查询等,同时数组可以随意存放在数组中任意位置,而线性表只能依次有序排列,不能出现空隙.
线性表的第一种实现: 顺序表
将数据一次存储在连续的整块物理空间中,这种存储称为顺序存储结构,而以这种方式实现的线性表,称为顺序表,表中的每一个个体都被称为元素,元素左边的元素(上一个元素),称为前驱,右边的元素(后一个元素)称为后驱.
抽象类
/**
* 线性表抽象类
* @parom 存储的元素(Element)类型
*/
public abstract class AbstractList<E>{
/*
* 获取表的长度
* @return 顺序表的长度
*/
public abstract int size();
/*
* 添加一个元素
* @param e 元素
* @param index 要添加的位置
*/
public abstract void add(E e,int index);
/**
* 移除指定位置的元素
* @param e 元素
* @return 要移除的元素
*/
public abstract E remove(int index);
/*
* 获取指定位置的元素
* @param index 位置
* @return 元素
*/
public abstract E get(int index);
}
实现:
package 顺序表;
public class MyList<E> extends AbstractList<E> {
//底层数据
private Object[] arr = new Object[20];
//长度
private int size = 0;
@Override
public int size() {
return size;
}
@Override
//插入
public void add(E e, int index) {
if (index > size) throw new IllegalStateException("非法的插入位置错误");//位置是否合法
if (size >= arr.length) { //扩容
Object[] ace = new Object[this.arr.length + 10];//局部
for (int i = 0; i < this.arr.length; i++) {
ace[i] = this.arr[i];
}
this.arr = ace;
}
int i = size - 1;
while (i >= index) { //后移后面的元素
arr[i + 1] = arr[i];
i--;
}
arr[index] = e;
size++;
}
@Override
//移除
public E remove(int index) {
if (index > size - 1) throw new IllegalStateException("非法删除位置错误");//位置是否合法
int i = index;
E e = (E) arr[i];
while (i < size - 1) {
arr[i] = arr[i + 1];
i++;
}
size--;//减少一个容量
return e;
}
@Override
public E get(int index) {
if (index >= size ) throw new IndexOutOfBoundsException("无法访问到下标位置");//位置是否合法
return (E) arr[index];
}
}
测试:
package 顺序表;
public class Main {
public static void main(String[] args) {
MyList<Integer> list=new MyList<>();
//添加
list.add(25,0);
list.add(34,1);
list.add(57,2);
list.add(16,3);
list.add(48,4);
list.add(9,5);
list.add(63,6);
list.add(50,3);
System.out.println(list.toString());
//删除
list.remove(3);
System.out.println(list.toString());
}
}
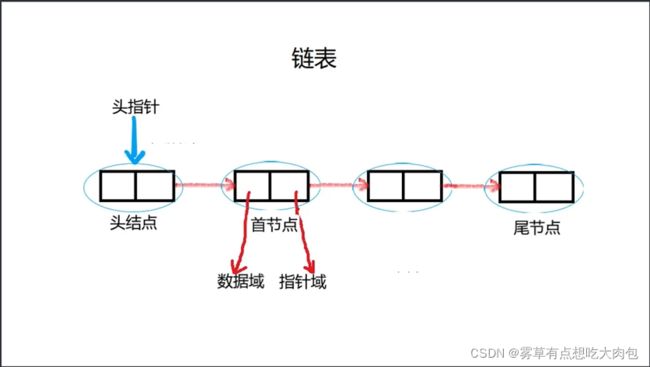
线性表的第二种实现: 链表
数据分散的存储在物理空间中,通过一根线保护着他们之间的逻辑关系,这种存储结构称为 链式存储结构,就是每一个结点存放一个元素和一个指向下一个结点的引用(C语言里面是指针,Java中就是对象的引用,代表下一个结点对象)
抽象类:
package 链表;
/*
* 线性表抽象类
* @param 存储的元素(Element)类型
*/
public abstract class AbstractList<E> {
/*
* 获取表的长度
* @return 顺序表的长度
*/
public abstract int size();
/*
* 添加一个元素
* @param e 元素
* @param index 要添加的位置
*/
public abstract void add(E e, int index);
/*
* 移除指定位置的元素
* @param E 元素
* @return 要移除的元素
*/
public abstract E remove(int index);
/*
* 获取指定位置的元素
* @param index 位置
* @return 元素
*/
public abstract E get(int index);
}
利用这种思想,我们来尝试实现上面的抽象类
实现类:
package 链表;
public class LinkedList<E> extends AbstractList<E> {
//头节点
private Node<E> head = new Node<>(null);
private int size = 0;
@Override
public int size() {
return size;
}
@Override
//插入结点
public void add(E e, int index) {
if (size < index) throw new IllegalArgumentException("非法插入位置");
Node<E> node = head, temp;//head前驱节点 temp存放后一个节点的引用
//index=1
for (int i = 0; i < index; i++)
node = node.next;
temp = node.next;//拿到后一个节点的引用
node.next = new Node<>(e);//新的节点
node.next.next = temp;
size++;
}
@Override
//删除结点
public E remove(int index) {
if (size - 1 < index) throw new IllegalArgumentException("非法插入位置");
Node<E> node = head, temp;
for (int i = 0; i < index; i++)
node = node.next;
temp = node.next;
node.next = node.next.next;
return temp.e;
}
@Override
public E get(int index) {
if (size <= index) throw new IllegalArgumentException("非法插入位置");
Node<E> node = head.next;
for (int i = 0; i < index; i++)
node = node.next;
return node.e;
}
private static class Node<E> {//内部类
private E e;//e一个元素一个节点
private Node<E> next; //下一个节点的引用
public Node(E e) {
this.e = e;
}
}
}
测试:
package 链表;
public class Main {
public static void main(String[] args) {
AbstractList<String> list=new LinkedList<>();
list.add("A",0);
list.add("B",1);
list.add("C",2);
list.remove(2);
System.out.println(list.get(1));
}
}
比较:顺序表和链表的异同点?
顺序表优缺点:
- 访问速度块,随机访问性能高
- 插入和删除的效率地下, 极端情况需要变更整个表
- 不易扩充,需要复制并重新创建数组
链表优缺点:
- 插入和删除效率搞,只需要改变连接点的指向即可
- 动态扩充容量,无需担心容量问题
- 访问元素需要依次寻找,随机访问元素效率底下
- 双项链表可以解决链表只能指向后面的问题
栈
栈和队列实际上就是对线性表加以约束的一种数据结构
栈遵循先入后出,或者叫后进先出,只能在线性表的一段添加和删除元素.我们可以把栈看作一个杯子,杯子只有一个口进出,最低处的元素只有等到上面杯子后,才能离开.
向栈中插入一个元素时,称为入栈,移除栈顶元素称为出栈,我们需要尝试实现一下抽象类型:
抽象类
package 栈;
/*
* 抽象类型栈,待实现
* @param 元素类型
*/
public abstract class AbstractStack<E> {
/*
* 出栈操作
* @return 栈顶元素
*/
public abstract E pop();
/*
*
* 入栈操作
* @param e 元素
*/
public abstract void push(E e);
}
实现类用顺序表实现:
package 栈;
public class ArrayStack<E> extends AbstractStack<E> {
//底层数组
private Object[] arr = new Object[20];
//长度
private int size = 0;
@Override
//压栈
public void push(E e) {
if (size >= arr.length) { //扩容
Object[] ace = new Object[this.arr.length + 10];//局部
for (int i = 0; i < this.arr.length; i++) {
ace[i] = this.arr[i];
}
this.arr = ace;
}
arr[size++] = e;//添加内容
}
@Override
//出栈
public E pop() {
return (E) arr[(size--) - 1];
}
}
测试:
package 栈;
public class Main {
public static void main(String[] args) {
ArrayStack<String> stack=new ArrayStack<>();
stack.push("A");
stack.push("B");
stack.push("C");
stack.pop();
stack.push("D");
System.out.println("debug");
}
}
(E) arr[(size–) - 1];
}
}
### 测试:
```java
package 栈;
public class Main {
public static void main(String[] args) {
ArrayStack stack=new ArrayStack<>();
stack.push("A");
stack.push("B");
stack.push("C");
stack.pop();
stack.push("D");
System.out.println("debug");
}
}