使用scikit-learn构建模型

1 绪论

1.1 机器学习的概念

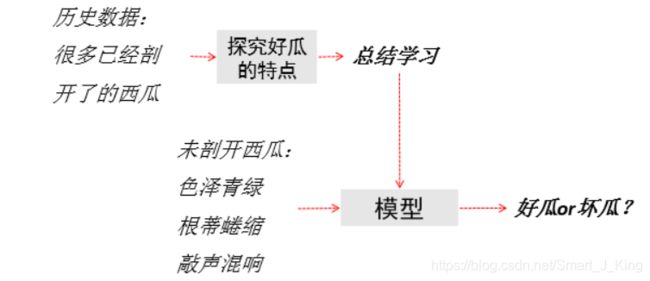
致力于研究如何通过计算的手段，利用经验（历史数据）来改善系统自身的性能［机器学习］。

从数据中产生模型的算法，即“学习算法”

机器学习的应用如股票预测、垃圾邮件过滤软件等。

1.2 scikit-learn

scikit-learn(sklearn)库整合了多种机器学习算法，可以帮助使用者在数据分析过程中快速建立模型，且模型接口统一，使用起来非常方便。同时，sklearn拥有优秀的官方文档（https://www.cntofu.com/book/170/index.html），知识点详尽，内容丰富，是入门学习sklearn的最佳内容。

2 使用sklearn转换器处理数据

2.1 加载datasets模块中数据集

sklearn库的datasets模块集成了部分数据分析的经典数据集，可以使用这些数据集进行数据预处理，建模等操作，熟悉sklearn的数据处理流程和建模流程。

datasets模块常用数据集的加载函数与解释如下表所示。加载后的数据集可以视为一个字典，几乎所有的sklearn数据集均可以使用data，target，feature_names，DESCR分别获取数据集的数据，标签，特征名称和描述信息。

• load_boston：波士顿房价数据
• load_iris：鸢尾花数据
• load_breast_cancer：威斯康辛州乳腺癌数据

#------------1.1加载datasets模块中数据集
from sklearn.datasets import load_boston #sklearn库安装命令：pip install scikit-learn -i https://mirrors.aliyun.com/pypi/simple

boston = load_boston() #加载波士顿房价数据
X = boston['data'] #特征数据
y = boston['target'] #标签数据
print('特征数据形状为：', X.shape)
print('标签数据形状为：', y.shape)

2.2 将数据集划分为训练集和测试集

常用划分方式：

在数据分析过程中，为了保证模型在实际系统中能够起到预期作用，一般需要将样本分成独立的三部分：

• 训练集（train set）：用于估计模型。
• 验证集（validation set)：用于确定网络结构或者控制模型复杂程度的参数。
• 测试集（test set）：用于检验最优的模型的性能。

典型的划分方式是训练集占总样本的50％，而验证集和测试集各占25％。一般的模型也可直接划分为训练集和测试集即可。

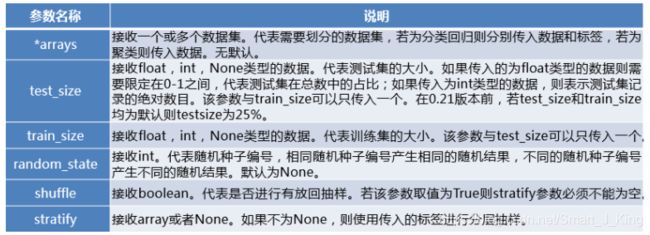
sklearn的model_selection模块提供了train_test_split函数，能够对数据集进行拆分，其使用格式如下：

sklearn.model_selection.train_test_split(*arrays, **options)

• train_test_split函数根据传入的数据，分别将传入的数据划分为训练集和测试集。
• 如果传入的是1组数据，那么生成的就是这一组数据随机划分后训练集和测试集，总共2组。如果传入的是2组数据，则生成的训练集和测试集分别2组，总共4组。
• train_test_split是最常用的数据划分方法，在model_selection模块中还提供了其他数据集划分的函数，如PredefinedSplit，ShuffleSplit等。

#------------1.2将数据集划分为训练集和测试集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) #按8:2的比例划分为训练集和测试集
print('训练集的特征数据形状为：', X_train.shape)
print('测试集的特征数据形状为：', X_test.shape)
print('训练集的标签数据形状为：', y_train.shape)
print('测试集的标签数据形状为：', y_test.shape)

2.3 使用sklearn转换器进行数据预处理与降维

2.3.1 数据预处理

使用sklearn进行数据预处理会用到sklearn提供的统一接口——转换器（Transformer）。

sklearn把相关的功能封装为转换器（transformer）。使用sklearn转换器能够实现对传入的NumPy数组进行标准化处理，归一化处理，二值化处理，PCA降维等操作。转换器主要包括三个方法：

在数据分析过程中，各类特征处理相关的操作都需要对训练集和测试集分开操作，需要将训练集的操作规则，权重系数等应用到测试集中。如果使用pandas，则应用至测试集的过程相对烦琐，使用sklearn转换器可以解决这一困扰。使用sklearn转换器，就是直接用fit方法去对训练集提取相应特征，通过transform分别对训练集和测试集应用一个相应的规则。

sklearn部分预处理函数与其作用：

#------------1.3使用sklearn转换器进行数据预处理与降维
#----1.3.1预处理
#--离差标准化处理
from sklearn.preprocessing import MinMaxScaler

minmaxscaler = MinMaxScaler().fit(X_train) #提取特征，生成规则
X_train_scaler = minmaxscaler.transform(X_train) #转换特征，应用规则
X_test_scaler = minmaxscaler.transform(X_test) #转换特征，应用规则
#利用训练集生成规则，之后便可这个规则同时应用于训练集和测试集


#--标准差标准化处理
from sklearn.preprocessing import StandardScaler

standardscaler = StandardScaler().fit(X_train) #提取特征，生成规则
X_train_standard = standardscaler.transform(X_train) #转换特征，应用规则
X_test_standard = standardscaler.transform(X_test)

2.3.2 PCA降维算法

sklearn除了提供基本的特征变换函数外，还提供了降维算法，特征选择算法，这些算法的使用也是通过转换器的方式。

PCA降维算法函数常用参数及其作用：

#----1.3.2降维
from sklearn.decomposition import PCA

pca = PCA(n_components=8).fit(X_train_standard) #生成规则
X_train_standard_8 = pca.transform(X_train_standard) #应用规则
X_test_standard_8 = pca.transform(X_test_standard)
print('X_train_standard_8的形状为：', X_train_standard_8.shape)
print('X_test_standard_8的形状为：', X_test_standard_8.shape)

3 构建并评价聚类模型

3.1 聚类

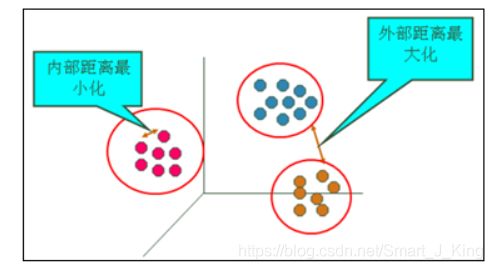
聚类的输入是一组未被标记的样本，聚类根据数据自身的距离或相似度将他们划分为若干组，划分的原则是组内样本最小化而组间（外部）距离最大化，如图所示。

聚类其实就是只拿特征数据用来构建模型。

聚类的应用：航空公司客户价值分析（根据客户信息“会员入会时间”、“最近坐飞机的时间”、“乘坐飞机次数”、“飞行里程”等特征，将客户划分成重要保持客户、重要发展客户、重要挽留客户、一般客户、低价值客户）。

3.2  聚类方法类别

sklearn常用的聚类算法模块cluster提供的聚类算法及其适用范围如下所示：

3.3 K-Means（聚类算法）

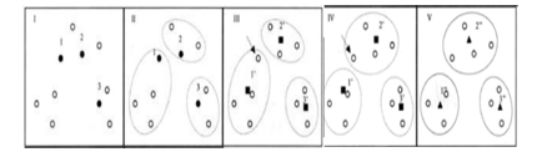
算法步骤：

（1）随机选取K个样本作为类中心；

（2）计算各样本与各类中心的距离；

（3）将各样本归于最近的类中心点；

（4）求各类的样本的均值，作为新的类中心；

（5）判定：若类中心不再发生变动或达到迭代次数，算法结束，否则回到第2步。

3.4 sklearn估计器

聚类算法实现需要sklearn估计器（estimator）。sklearn估计器和转换器类似，拥有fit和predict两个方法。两个方法的作用如下。

3.5 聚类模型评价指标

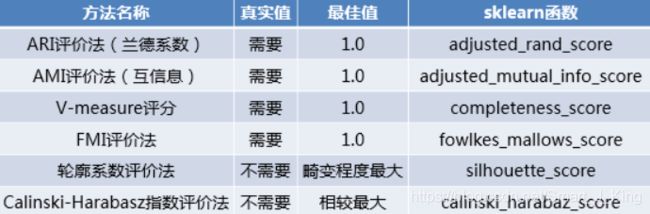
聚类评价的标准是组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。即组内的相似性越大，组间差别越大，聚类效果就越好。sklearn的metrics模块提供的聚类模型评价指标。

• 优劣，后2种则不需要真实值的配合。但是前4种方法评价的效果更具有说服力，并且在实际运行的过程中在有真实值做参考的情况下，聚类方法的评价可以等同于分类算法的评价。
• 除了轮廓系数以外的评价方法，在不考虑业务场景的情况下都是得分越高，其效果越好，最高分值均为1。而轮廓系数则需要判断不同类别数目的情况下其轮廓系数的走势，寻找最优的聚类数目。
• 在具备真实值作为参考的情况下，几种方法均可以很好地评估聚类模型。在没有真实值作为参考的时候，轮廓系数评价方法和Calinski-Harabasz指数评价方法可以结合使用。

#==================2构建并评价聚类模型(构建模型时仅需要有特征数据）
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import calinski_harabasz_score

iris = load_iris() #加载鸢尾花数据
data = iris['data'] #特征数据

#构建KMeans模型并训练
model = KMeans(n_clusters=3).fit(data)
model.labels_ #聚类标签
model.cluster_centers_ #聚类中心
#预测
model.predict([[4.0, 2.7, 1.8, 0.4]])


#聚类可视化
plt.scatter(data[model.labels_==0, 0], data[model.labels_==0, 1])
plt.scatter(data[model.labels_==1, 0], data[model.labels_==1, 1])
plt.scatter(data[model.labels_==2, 0], data[model.labels_==2, 1])
plt.legend([0, 1, 2])
plt.show()

#指数评价法
calinski_harabasz_score(data, model.labels_)

3 构建并评价分类模型

3.1 分类算法的实现过程

在数据分析领域，分类算法有很多，其原理千差万别，有基于样本距离的最近邻算法，有基于特征信息熵的决策树，有基于bagging的随机森林，有基于boosting的梯度提升分类树，但其实现的过程相差不大。过程如图所示：

分类的应用：垃圾短信的识别。

3.2 sklearn库常用分类算法函数

sklearn中提供的分类算法非常多，分别存在于不同的模块中。常用的分类算法如下表所示：

3.3 支持向量机（分类算法）

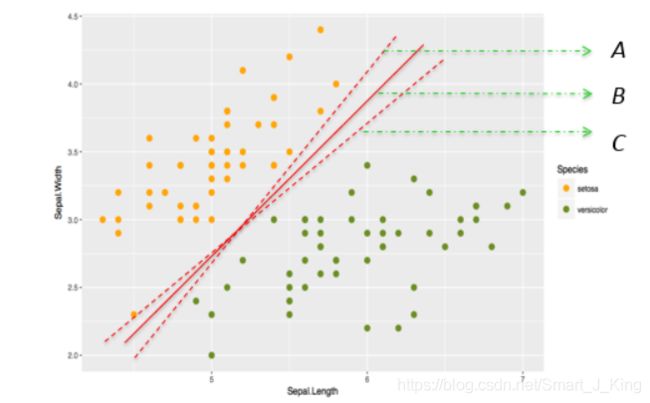
支持向量机的原理是寻找一条线（超平面）能够很好地区分两类样本。

最优超平面(直线)：对训练样本局部扰动的“容忍性”最好，即最具鲁棒性。

3.4 分类模型的评价指标

分类模型对测试集进行预测而得出的准确率并不能很好地反映模型的性能，为了有效判断一个预测模型的性能表现，需要结合真实值，计算出精确率、召回率、F1值和Cohen’s Kappa系数等指标来衡量。常规分类模型的评价指标如表所示。分类模型评价方法前4种都是分值越高越好，其使用方法基本相同。

sklearn的metrics模块还提供了一个能够输出分类模型评价报告的函数classfication_report。

ROC曲线

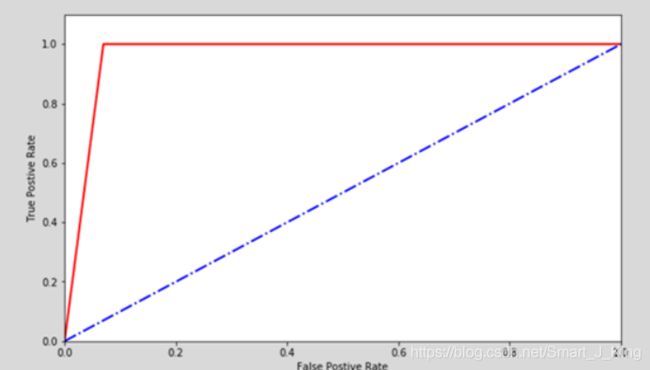
除了使用数值，表格形式评估分类模型的性能，还可通过绘制ROC曲线的方式来评估分类模型。

ROC曲线横纵坐标范围为[0,1]，通常情况下ROC曲线与X轴形成的面积越大，表示模型性能越好。但是当ROC曲线处于下图中蓝色虚线的位置，就表明了模型的计算结果基本都是随机得来的，在此种情况下模型起到的作用几乎为零。故在实际中ROC曲线离图中蓝色虚线越远表示模型效果越好。

#==================3构建并评价分类模型(构建模型时需要有特征数据和标签数据，标签数据是离散型，即类别型的）
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt

#----3.1加载数据
cancer = load_breast_cancer() #加载乳腺癌数据
X = cancer['data'] #特征数据
y = cancer['target'] #标签数据
X.shape #(569, 30)
y.shape #(569,)

#----3.2划分数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) #按8:2的比例划分为训练集和测试集
X_train.shape #(455, 30)
X_test.shape #(114, 30)
y_train.shape #(455,)
y_test.shape #(114,)

#----3.3标准化数据
np.int32(X_train.max(axis=0)) #量纲差异大

##标准差标准化
scaler = StandardScaler().fit(X_train) #生成规则
X_train = scaler.transform(X_train) #应用规则
X_test = scaler.transform(X_test)

#----3.4构建svm模型并训练
model = SVC().fit(X_train, y_train)

#----3.5预测
pre = model.predict(X_test)

#----3.6评价模型
#--准确率
sum(y_test == pre)/len(y_test) #0.9824561403508771
#--ROC曲线评价法
fpr, tpr, thresholds = roc_curve(y_test, pre) #fpr表假正率，tpr表真正率，thresholds表阈值
plt.plot(fpr, tpr) #越靠近与y轴效果越好
plt.show()

4 构建并评价回归模型

4.1 回归分析方法

从19世纪初高斯提出最小二乘估计算起，回归分析的历史已有200多年。从经典的回归分析方法到近代的回归分析方法。

按照研究方法划分，回归分析研究的范围大致如图所示。

回归算法的实现步骤和分类算法基本相同，分为学习和预测2个步骤。学习是通过训练样本数据来拟合回归方程；预测则是利用学习过程中拟合出的回归方程，将测试数据放入方程中求出预测值。

回归的应用：房价预测。

4.2 常用的回归模型

4.3 sklearn库常用回归算法函数

sklearn内部提供了不少回归算法，常用的函数如下表所示。

可以利用预测结果和真实结果画出折线图作对比，以便更直观看出线性回归模型效果。

4.4 线性回归（回归算法）

线性模型试图学得一个通过属性的线性组合来进行预测（目标属性）的函数。

4.5 回归模型评价指标

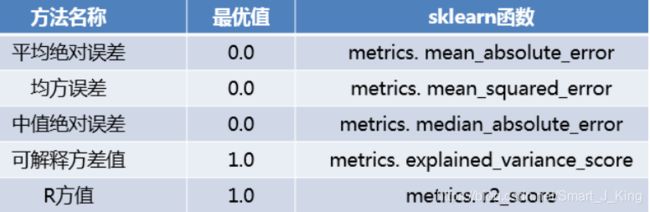
回归模型的性能评估不同于分类模型，虽然都是对照真实值进行评估，但由于回归模型的预测结果和真实值都是连续的，所以不能够求取Precision、Recall和F1值等评价指标。回归模型拥有一套独立的评价指标。

平均绝对误差、均方误差和中值绝对误差的值越靠近0，模型性能越好。可解释方差值和R方值则越靠近1，模型性能越好。

#==================4构建并评价回归模型(构建模型时需要有特征数据和标签数据，标签数据是连续型数据）
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score

#----4.1加载数据
boston = load_boston() #加载波士顿房价数据
X = boston['data'] #特征数据
y = boston['target'] #标签数据

#----4.2划分数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) #按8:2的比例划分为训练集和测试集

#----4.3构建线性回归模型并训练
model = LinearRegression().fit(X_train, y_train)

#----4.4预测
pre = model.predict(X_test)

#----4.5可视化(可有可无）
##绘制真实值折线图
plt.plot(range(len(y_test)), y_test)
##绘制预测值折线图
plt.plot(range(len(pre)), pre)
plt.legend(['real', 'pre'])
plt.show()

#----4.6模型评价
r2_score(y_test, pre)