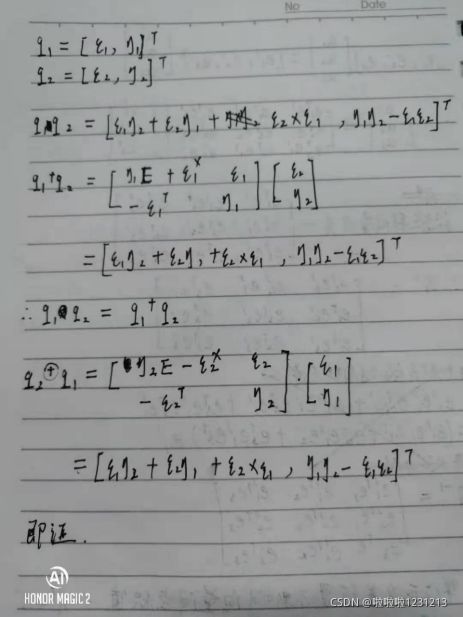视觉slam学习笔记以及课后习题《第二讲三维物体刚体运动》

前言

这篇博客主要记录了我在深蓝学院视觉slam课程中的课后习题，因为是为了统计知识点来方便自己以后查阅，所以有部分知识可能不太严谨，如果给大家造成了困扰请见谅，大家发现了问题也可以私信或者评论给我及时改正，欢迎大家一起探讨。其他章节的笔记和作业可以在我的首页中查找对应文章。

整个作业的代码和文档都可以参考我的GitHub存储库https://github.com/1481588643/vslam.git

如果还想了解视觉slam其他章节的内容可以参考如下链接：视觉slam学习笔记以及课后习题《第一讲初识slam》_m0_61238051的博客-CSDN博客

视觉slam学习笔记以及课后习题《第三讲李群李代数》_m0_61238051的博客-CSDN博客

https://blog.csdn.net/m0_61238051/article/details/120813741

一.熟悉 Eigen 矩阵运算 (2 分，约 2 小时)

Eigen（http://eigen.tuxfamily.org）是常用的 C++ 矩阵运算库，具有很高的运算效率。大部分需要在 C++ 中使用矩阵运算的库，都会选用 Eigen 作为基本代数库，例如 Google Tensorflow，Google Ceres，GTSAM 等。本次习题，你需要使用 Eigen 库，编写程序，求解一个线性方程组。为此，你需要先了解一些有关线性方程组数值解法的原理。

设线性方程 Ax = b，在 A 为方阵的前提下，请回答以下问题：

1.在什么条件下，x 有解且唯一？

答：当A为方阵且A可逆（即A满秩），x有解且唯一。

2.高斯消元法的原理是什么？

答：高斯消元法(Gaussian elimination)是求解线性方程组的一种算法，它也可用来求矩阵的秩，以及求可逆方阵的逆矩阵。它通过逐步消除未知数来将原始线性系统转化为另一个更简单的等价的系统。

原理：通过初等行变化将线性方程组的增广矩阵转化为行阶梯矩阵（上三角或下三角矩阵）。通过初等行变换把A编程阶梯矩阵求解

求解过程：

1.构造增广矩阵，即系数矩阵A增加上常数向量b(A|b).

2.通过以交换行、某行乘以非负常数和两行相加这三种初等变化将原系统转化为更简单的三角形式(**triangular form**) 注:这里的初等变化可以通过系数矩阵A乘上初等矩阵E来实现。

从而得到简化的三角方阵组，这样就容易解了

3.最后再使用向后替换算法(Algorithm for Back Substitution)求解得。

3.QR 分解的原理是什么？

答： 将A分解成正交矩阵和上三角矩阵的乘积A=QR，易解Ra=Q^Tb
原理：利用２个正交矩阵的乘积一定是正交矩阵，正交矩阵的逆矩阵也是正交矩阵的特点，对正交矩阵进行多次分解，相乘。QR分解的原理主要是把矩阵分解成一个列向量正交矩阵与一个上三角矩阵的迹，原理是将矩阵每个列作为一个基本单元，将其化为正交的基向量，与在这个基向量上的投影长度的QR分解，经常用来解决最小回归问题，也是特征值算法QR算法的基础。

求解过程：

1.对需要求解的特征值的矩阵A进行QR分解；

2.对分解出来的结果进行逆向相乘；

3.将相乘得到的矩阵进行QR分解；

4.对分解出来的结果进行逆向相乘；

4.Cholesky 分解的原理是什么？

答：

定义：如果矩阵A为n阶对称正定矩阵，则存在一个对角元素为正数的下三角实矩阵L，使得：\(A=LL^T\)，当限定L的对角元素为正时，这种分解是唯一的，称为Cholesky分解。
cholesky分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的。Cholesky分解法又称平方根法，是当A为实对称正定矩阵时，LU三角分解法的变形

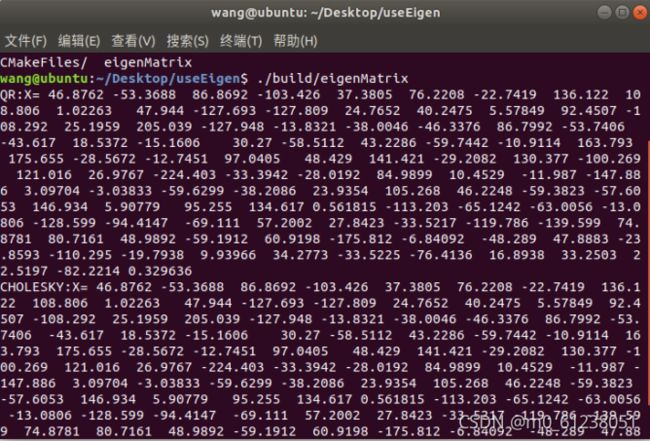
5.编程实现 A 为 100 × 100 随机矩阵时，用 QR 和 Cholesky 分解求 x 的程序。你可以参考本次课用到的 useEigen 例程。

提示：你可能需要参考相关的数学书籍或文章。请善用搜索引擎。Eigen 固定大小矩阵最大支持到 50， 所以你会用到动态大小的矩阵。

​

#include
#include
#include
using namespace Eigen;
using namespace std;
int size=100;

int main(int argc, char const *argv[])
{

MatrixA;
A=MatrixXd::Random(size,size);
A=A*A.transpose();
 Matrix B;
B=MatrixXd::Random(size,1);
MatrixX;
X=A.colPivHouseholderQr().solve(B);
     cout<<"QR:X="<
 
  

二.矩阵论基础 （ 分，约 2 小时）

除了我们本科学过的基础线性代数之外，大部分研究生课程还会开设矩阵论课程，以作为对本科阶段  知识的扩充。对于很多线性问题（SLAM  里也会碰到许多线性问题），了解一些矩阵论基础知识是很有好处的。我们在附件中为大家提供了张贤达老师的《矩阵分析与应用》。请参考该书内容（或者你能找到的其 他书籍），回答以下问题。

1.什么是正定矩阵和半正定矩阵？

答：给定一个n乘以n的实对称矩阵A，若对于任意长度为 n 的非零向量 x，有 x的转置乘以A再乘以x恒大于0，则矩阵 A 是一个正定矩阵。

给定一个n乘以n的实对称矩阵A，若对于任意长度为 n 的非零向量 x，有 x的转置乘以A再乘以x恒大于等于0，则矩阵 A 是一个正定矩阵。

2.对于方阵 A，它的特征值是什么？特征向量是什么？特征值一定是实数吗？如何计算一个矩阵的特征值？

答：设A为n阶实方阵，如果存在某个数 及某个n维非零列向量，使得，则称是方阵A的一个特征值，是方阵A的属于特征值的一个特征向量。

设A为n阶实方阵， 为一个参数，称n阶方阵为A的特征方阵，它的行列式称为A的特征多项式，把称为A的特征方程，把特征方程或特征多项式的根称为A的特征根。

特征值不一定是实数，也可能是虚数。

3.什么是矩阵的相似性？相似性反映了什么几何意义？

答：在线性代数中，相似矩阵（英语：similar matrix）是指存在相似关系的矩阵。相似关系是两个矩阵之间的一种等价关系。两个n×n矩阵A与B为相似矩阵当且仅当存在一个n×n的可逆矩阵P，使得：{P^{-1}AP=B}

P被称为矩阵A与B之间的相似变换矩阵。

相似的矩阵是同一个线性变换在不同基/坐标系下的的不同描述。
线性变换若粗略看成一个刚体的特定运动。刚体的特定运动是同一个，但坐标系改变的话这个运动的描述函数就会不一样，如果这个函数可用矩阵等价替代的话，一个坐标系就对应着一个矩阵，因此这些矩阵就不同，但这些矩阵必有关系，这个关系就是相似。

4.矩阵一定能对角化吗？什么样的矩阵能保证对角化？不能对角化的矩阵能够形成什么样的形式（Jor- dan 标准形）？

答：矩阵不一定能对角化，n阶方阵可对角化的充分必要条件是它有n个线性无关的特征向量。不能对角化的矩阵一定具有多重特征值，对于不能对角化的矩阵也希望找到某种标准形式，使之尽量接近对角化的形式——Jordan标准形。

5.奇异值分解（SVD）是什么意思？

答：奇异值分解（SVD）是一种用于将矩阵归约成其组成部分的矩阵分解方法，以使后面的某些矩阵计算更简单。

X=UΣV∗,X=UΣV∗,
其中U是m×m阶酉矩阵；Σ是m×n阶非负实数对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作X的奇异值分解。

6.矩阵的伪逆是什么意思（Pseudo inverse）？莫尔——彭多斯逆是如何定义的？怎么计算一个矩阵的伪逆？

答：对于矩阵A，如果存在一个矩阵B，使得AB=BA=I，其中I为与A,B同维数的单位阵，就称A为可逆矩阵（或者称A可逆），并称B是A的逆矩阵，简称逆阵。（此时的逆称为凯利逆）矩阵A可逆的充分必要条件是|A|≠0。奇异矩阵阵或非方阵的矩阵不存在逆矩阵，但可以用函数pinv(A)求其伪逆矩阵。基本语法为X=pinv(A),X=pinv(A,tol),其中tol为误差：max(size(A))*norm(A)*eps。函数返回一个与A的转置矩阵A'同型的矩阵X，并且满足：AXA=A,XAX=X.此时，称矩阵X为矩阵A的伪逆，也称为广义逆矩阵。pinv(A)具有inv(A)的部分特性，但不与inv(A)完全等同。

设 A∈Cm*n,若存在矩阵G∈Cn*m（C为复数域）,使得
(1) AGA = A;
(2) GAG = G;
(3) (AG)H = AG;
(4) (GA)H = GA;
则称 G 为 A 的Moore-Penrose广义逆或加号广义逆，简称为A的M-P逆。A的任意M-P逆记为A+。

7. 对于超定方程：Ax = b A 不可逆时，我们通常计算最小二乘解：x = arg minx

Ax − b 。线性方程的最小二乘解在代数意义上是可以解析地写出来的。请回答以下小问题：

7.1 在 b ̸= 0 时，x 的解是什么形式？事实上，我们可以对 A 求奇异值或对于 ATA 求特征值。请阐述两者之间的关系。

答：对于超定方程Ax = 0的解就是 ATA 最小特征值对应的特征向量。

简单的讲　所有的矩阵都可以进行奇异值分解，不管其是否是方阵以及对称矩阵。当所给的矩阵是对称的方阵，A(T)=A，二者的结果是相同的。也就是说对称矩阵的特征值分解是所有奇异值分解的一个特例。

但是二者还是存在一些小的差异，奇异值分解需要对奇异值从大到小的排序，而且全部是大于等于零。

特征值用来描述方阵，可看做是从一个空间到自身的映射，这也表现在了名字eigenvalue中。奇异值可以描述长方阵或奇异矩阵，可看做是从一个空间到另一个空间的映射。

7.2  当 b = 0 时，我们希望求 x 的非零解。请说明如何求解 x。

答：对于超定方程Ax = 0的解就是 ATA 最小特征值对应的特征向量。

7.3   请谈谈你对上述解法在几何意义上的理解。该问题为开放问题。

答：首先考虑一个简单的超定方程组

该方程组的右端向量是三维向量，系数矩阵的每一列也是三维向量，但待求的未知向量却是二维向量。将系数矩阵按列分块，G =[a1，a2]，记右端向量为b。则方程组求解问题可表示为求组合系数x和y使

xa1 + ya2 = b

的向量的线性组合问题。由于两个向量a1，a2不构成三维空间的一组基，所以一般情况下这一问题无解。而由向量a1，a2张成的子空间span{a1，a2}是一张平面，记为p。则超定方程组的最小二乘解实际上是求X*，使GX* 恰好等于b 在平面p上的投影。而最小二乘解所对应的残差向量则垂直于向量GX*。事实上，由正规方程组

GTGX=GTb

得

GT (b –GX * ) = 0

上式的几何意义可解释为：最小二乘解的残差向量与超定方程组的系数矩阵G的所有列向量正交。从而

(X*)T GT (b –GX * ) = 0

所以

(GX *，b –GX * ) = 0

三.几何运算练习 (2 分，约 1 小时)

下面我们来练习如何使用 Eigen/Geometry 计算一个具体的例子。

 一个机器人上通常会安装许多不同的传感器，而 这些传感器之间还存在固连关系。我们举一个典型的例子。

在世界系 W 下，存在一个运动的机器人 R。按照固定的或者某些开发人员或者领导的特殊喜好，R 系定义在机器人脚部的位置。但是机器人在设计的时候，又定义了 B 系（Body 系，或本体系），位于机器人头部的位置。由于沟通不畅，标定人员把一台激光传感器和一台视觉传感器标定在了 B 系下。我们称激光传感器为 L 系，视觉传感器为 C 系。现在请你完成以下工作：

1. 说明一个激光传感器下的看到的点应该如何计算它的世界坐标。

 2.  取：qW R = [0.55, 0.3, 0.2, 0.2], tW R = [0.1, 0.2, 0.3]T ，qRB = [0.99, 0, 0, 0.01], tRB = [0.05, 0, 0.5]T ，

qBL = [0.3, 0.5, 0, 20.1], tBL = [0.4, 0, 0.5]T , qBC = [0.8, 0.2, 0.1, 0.1], tBC = [0.5, 0.1, 0.5]T 。现在假

设相机传感器观察到自身坐标系下的点 [0.3, 0.2, 1.2]，请计算：

(a)这个点在激光系下的坐标； (b)这个点在世界系下的坐标。

提示：

1. 本题的数据是随意取的，没有真实意义，产生什么结果都不要奇怪。
2. 四元数在使用前需要归一化。
3. 请注意 Eigen 在使用四元数时的虚部和实部顺序。

PS:注意这道题的坐标变换公式，要理清给的转换矩阵是那个坐标系到哪个坐标系的转换矩阵，比如T_WR就是机器人到世界坐标系下的转换矩阵，如果我知道一个在机器人坐标系下的点P_R，那么在世界坐标系下该点的坐标就是T_WR*P_R.

这道题给出的公式是这个点在激光系下的坐标为：P_L=T_BL.inverse()*T_BC*P_C

在世界坐标系下的转换公式为：P_W=T_WR*T_RB*T_BC*P_C

#include 

using namespace std;

#include 
#include 

using namespace Eigen;

int main(int argc, char ** argv){

    //创建视觉传感器和激光传感器的四元数
    Quaterniond q_BL(0.3, 0.5, 0,20.1), q_BC(0.8, 0.2, 0.1, 0.1);
    //四元数归一化
    q_BC.normalize();
    q_BL.normalize();

    //平移向量t1和t2
    Vector3d t_BL(0.4, 0, 0.5), t_BC(0.5, 0.1, 0.5);
    //p1坐标
    Vector3d p1(0.3, 0.2, 1.2);

    //变换矩阵Tc1w和Tc2w
    Isometry3d T_BL(q_BL), T_BC(q_BC);
    T_BL.pretranslate(t_BL);
    T_BC.pretranslate(t_BC);

    //计算p2
    Vector3d p2 = T_BL.inverse()*T_BC*p1;
    cout <<"这个点在激光系下的坐标"<< p2.transpose() << endl;
       Vector3d p23= T_BL*T_BC.inverse()*p1;
    cout <<"这个点在激光系下的坐标"<< p23.transpose() << endl;

  //创建世界系和机器人本体的四元数
    Quaterniond q3(0.55, 0.3, 0.2,0.2), q4(0.99, 0, 0, 0.01);
    //四元数归一化
    q3.normalize();
    q4.normalize();

    //平移向量t3和t4
    Vector3d t3(0.1, 0.2, 0.3), t4(0.05, 0, 0.5);


    //变换矩阵Tc3w和Tc4w
    Isometry3d Tc3w(q3), Tc4w(q4);
    Tc3w.pretranslate(t3);
    Tc4w.pretranslate(t4);

    //计算p3
    Vector3d p3 = Tc4w*Tc3w*Tc*p1;
    cout <<"这个点在世界系下的坐标"<< p3.transpose() << endl;


    return 0;
                                                                                                                                                                                          49,1         顶端

​

四.旋转的表达 （2 分，约 1 小时）

​

1.

​

 2.答：ε的维度是3，η的维度是1.

3.

​

五.罗德里格斯公式的证明 (1 分，约 1 小时)

罗德里格斯公式描述了从旋转向量到旋转矩阵的转换关系。设旋转向量长度为 θ，方向为 n，那么旋转矩阵 R 为：

R = cos θI + (1 − cos θ)nnT + sin θn∧. (4)

1.我们在课程中仅指出了该式成立，但没有给出证明。请你证明此式。提示：参考https://en.wikipedia. org/wiki/Rodrigues%27_rotation_formula。

​

2.请使用此式请明 R−1 = RT 。

​

六.四元数运算性质的验证 (1 分，约 1 小时)

​

​

七.*熟悉c++

​

第15行：使用了初始化列表来初始化对象： C++11 把初始化列表的概念绑定到了类型上，并将其称之为 std::initializer_list，允许构造函数或其他函数像参数一样使用初始化列表，这就为类对象的初始化与普通数组和 POD 的初始化方法提供了统一的桥梁。

第16行：使用了lambda表达式来比较元素大小，其中：const A&a1, const A&a2是参数列表，return a1.index

第17行：用auto关键字实现了自动类型推导，让编译器自动设置变量a的类型；

第17行：C++引入了基于范围的for循环，不用下标就能访问元素；