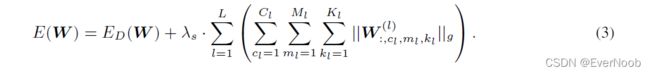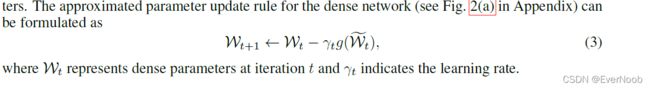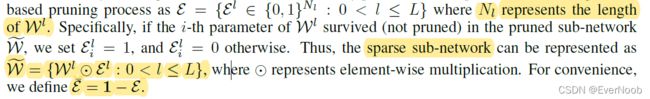Sparsity in Deep Learning

 SOTA* Overview

*[Submitted on 31 Jan 2021]

Sparsity in Deep Learning: Pruning and growth for efficient inference and training in neural networks

https://arxiv.org/abs/2102.00554

The growing energy and performance costs of deep learning have driven the community to reduce the size of neural networks by selectively pruning components. Similarly to their biological counterparts, sparse networks generalize just as well, if not better than, the original dense networks. Sparsity can reduce the memory footprint of regular networks to fit mobile devices, as well as shorten training time for ever growing networks. In this paper, we survey prior work on sparsity in deep learning and provide an extensive tutorial of sparsification for both inference and training. We describe approaches to remove and add elements of neural networks, different training strategies to achieve model sparsity, and mechanisms to exploit sparsity in practice. Our work distills ideas from more than 300 research papers and provides guidance to practitioners who wish to utilize sparsity today, as well as to researchers whose goal is to push the frontier forward. We include the necessary background on mathematical methods in sparsification, describe phenomena such as early structure adaptation, the intricate relations between sparsity and the training process, and show techniques for achieving acceleration on real hardware. We also define a metric of pruned parameter efficiency that could serve as a baseline for comparison of different sparse networks. We close by speculating on how sparsity can improve future workloads and outline major open problems in the field.

download pdf:

https://arxiv.org/pdf/2102.00554

a tutorial offered by the paper's authors from ETH Zürich 

Sparsity in Deep Learning Tutorial

the promised video link that was not added, a talk by Torsten Hoefler

https://www.youtube.com/watch?v=H7-p3OWPpEI

!!Hint!!

The "paper" is more like a pamphlet, with 90 pages in total. It might be better to start with the authors' tutorial or talk, which is only about 2hr long.

Use the paper for reference to details and reviews after the tutorial/talk session.

Early Paper: SSL

https://proceedings.neurips.cc/paper/2016/file/41bfd20a38bb1b0bec75acf0845530a7-Paper.pdf

Learning Structured Sparsity in Deep Neural Networks 

High demand for computation resources severely hinders deployment of large-scale Deep Neural Networks (DNN) in resource constrained devices. In this work, we propose a Structured Sparsity Learning (SSL) method to regularize the structures (i.e., filters, channels, filter shapes, and layer depth) of DNNs. SSL can: (1) learn a compact structure from a bigger DNN to reduce computation cost; (2) obtain a hardware-friendly structured sparsity of DNN to efficiently accelerate the DNN’s evaluation. Experimental results show that SSL achieves on average 5.1× and 3.1× speedups of convolutional layer computation of AlexNet against CPU and GPU, respectively, with off-the-shelf libraries. These speedups are about twice speedups of non-structured sparsity; (3) regularize the DNN structure to improve classification accuracy. The results show that for CIFAR-10, regularization on layer depth reduces a 20-layer Deep Residual Network (ResNet) to 18 layers while improves the accuracy from 91.25% to 92.60%, which is still higher than that of original ResNet with 32 layers. For AlexNet, SSL reduces the error by ∼ 1%.

Paper Notes

Issue with Previous Works

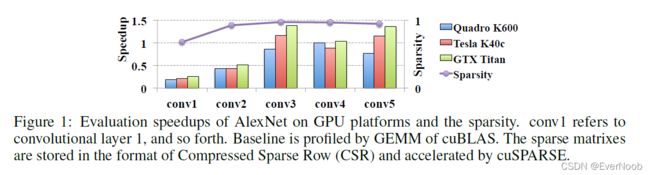
Sparsity regularization and connection pruning, however, often produce non-structured random connectivity and thus, irregular memory access that adversely impacts practical acceleration in hardware platforms. Figure 1 depicts practical layer-wise speedup of AlexNet, which is non-structurally sparsified by l1-norm. Compared to original model, the accuracy loss of the sparsified model is controlled within 2%. Because of the poor data locality associated with the scattered weight distribution, the achieved speedups are either very limited or negative even the actual sparsity is high, say, >95%.

==> low rank approximation is only layerwise structured and need extra steps to finetune for better performance and accuracy for the entire network.

==> response:

we propose Structured Sparsity Learning (SSL) method to directly learn a compressed structure of deep CNNs by group Lasso regularization during the training. SSL is a generic regularization to adaptively adjust multiple structures in DNN, including structures of filters,
channels, filter shapes within each layer, and structure of depth beyond the layers. SSL combines structure regularization (on DNN for classification accuracy) with locality optimization (on memory access for computation efficiency), offering not only well-regularized big models with improved accuracy but greatly accelerated computation

Lasso and Group Lasso ==> if not familiar with these regularizers, crucial to checkout group lasso and sparse group lasso

Ridge and Lasso Regression: L1 and L2 Regularization_EverNoob的博客-CSDN博客

Proposed structured sparsity learning for generic structures

==> sparse group lasso

lasso for unstructred learning and group lasso for structured learning

Structured sparsity learning for structures of filters, channels, filter shapes and depth

==> essentially just picking the granularity for pruning with group lasso

 figure 2

 

Structured sparsity learning for computationally efficient structures

==> just more computationally efficient granularity with

2D-filter:

The fine-grain version of filter-wise sparsity can more efficiently reduce the computation associated with convolution: Because the distance of weights (in a smaller group) from the origin is shorter ==> in the feature space, amounts to the same as a smaller shrinking factor, which makes group Lasso more easily to obtain a higher ratio of zero groups.

filter + shape for GEMM:

==> when using GEneral Matrix Multiplication, we are talking about img2col expanded FM and weight matrices.

Combining filter-wise and shape-wise sparsity can directly reduce the dimension of weight matrix in GEMM by removing zero rows and columns. In this context, we use row-wise and column-wise sparsity as the interchangeable terminology of filter-wise and shape-wise sparsity, respectively.

Summary

==> in essence, SSL introduce regularization terms to filter out weights by different granularities;

by the description of experiment setup:

 and by the conclusion:

we see that SSL only applied to inference improvements, as part of an extended training session, in terms of both speed and accuracy, but the regularizers cannot be confidently integrated into the initial training process itself. (The technique seems to be abled to be applied from scratch or introduced JIT-style, but the paper never explicitly discussed it.)

==> the next technique, however, can be applied to initial training.

STE and SR-STE

Learning N:M Fine-grained Structured Sparse Neural Networks From Scratch

https://arxiv.org/abs/2102.04010

Sparsity in Deep Neural Networks (DNNs) has been widely studied to compress and accelerate the models on resource-constrained environments. It can be generally categorized into unstructured fine-grained sparsity that zeroes out multiple individual weights distributed across the neural network, and structured coarse-grained sparsity which prunes blocks of sub-networks of a neural network. Fine-grained sparsity can achieve a high compression ratio but is not hardware friendly and hence receives limited speed gains. On the other hand, coarse-grained sparsity cannot concurrently achieve both apparent acceleration on modern GPUs and decent performance. In this paper, we are the first to study training from scratch an N:M fine-grained structured sparse network, which can maintain the advantages of both unstructured fine-grained sparsity and structured coarse-grained sparsity simultaneously on specifically designed GPUs. Specifically, a 2:4 sparse network could achieve 2x speed-up without performance drop on Nvidia A100 GPUs. Furthermore, we propose a novel and effective ingredient, sparse-refined straight-through estimator (SR-STE), to alleviate the negative influence of the approximated gradients computed by vanilla STE during optimization. We also define a metric, Sparse Architecture Divergence (SAD), to measure the sparse network's topology change during the training process. Finally, We justify SR-STE's advantages with SAD and demonstrate the effectiveness of SR-STE by performing comprehensive experiments on various tasks. Source codes and models are available at this https URL.

download pdf:

https://arxiv.org/pdf/2102.04010

Paper Notes

==> unstructured sparsity has the same issue as pointed by previous paper; structured sparsity has low compression rate

==> terminology

==> key point for this paper, which is also the key failure of SSL

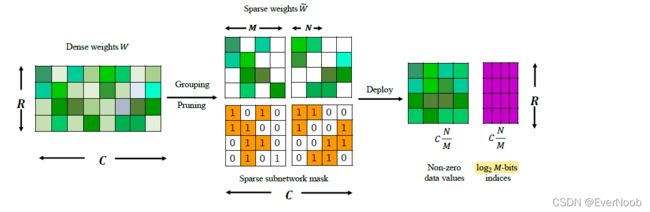
Nvidia has proposed an ASP1 (APEX’s Automatic Sparsity) solution (Nvidia, 2020) to sparsify a dense neural network to satisfy the 2:4 fine-grained structured sparsity requirement. The recipe contains three steps: (1) training a dense network until converge; (2) pruning for 2:4 sparsity with magnitude-based single-shot pruning; (3) repeating the original training procedure. However, ASP is computationally expensive since it requires training the full dense models from scratch and finetuning again. Therefore, we still lack a simple recipe to obtain a structured sparse DNN model consistent with the dense network without extra fine-tuning.

This paper addresses this question: Can we design a simple yet universal recipe to learn N:M sparse neural networks from scratch in an efficient way?

==> train sparse NN from scratch is called the one-stage scheme, which requires training for the sparsity and performance parameters in one go, and often result in lower model performance.

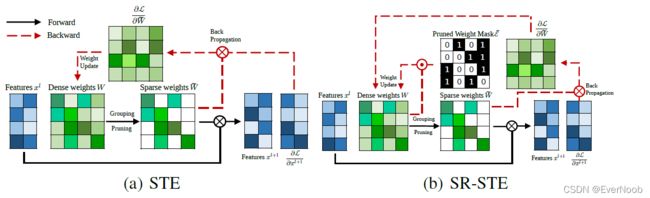
Straight Through Estimator 

==> a BP helper for un-differentiable functions, such as quantization

here for FP:

for BP:

 

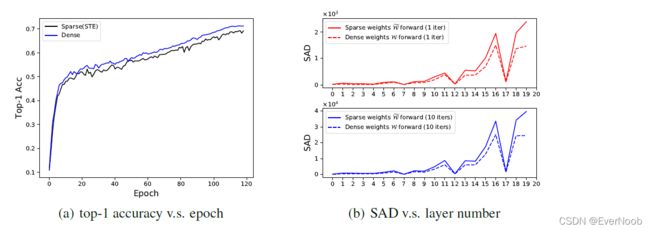
Sparse Architecture Divergence, SAD

==> pilot experiments shows that STE severely degrade performance, hence, introduce SAD

to measure architectural change. 

 definition of SAD

==> SAD is a good Architecture change measure

Before our defined SAD, (Liu et al., 2020) proposes Neural Network Sparse Topology Distance (NNSTD) to measure topological distances between two sparse neural networks. It is worth noting that NNSTD reorders the neurons in each layer, based on their connections to the previous layer, to maximize the similarities between the two compared networks’ topologies. Hence, NNSTD can only measure general topological differences between two networks but fails to reflect the transitions of individual connections’ states (pruned or not pruned). However, when calculating SAD, the mask for each connection is directly computed without neurons being ordered, hence SAD could provide more precise estimation of actual state changes (from being pruned to not pruned, and vice versa) of network connections, which is what we most concern about in this paper.

SPARSE-REFINED STRAIGHT-THROUGH ESTIMATOR (SR-STE)

In mathematics, the Hadamard product (also known as the element-wise product, entrywise product[1]: ch. 5  or Schur product[2])

==> why

Inspired by above observations made from SAD analysis, we aim to reduce SAD to improve the sparse network’s performance. Since the magnitude of parameter jwj are used as a metric to prune the network weights, we need to alternate the weight updating process in order to prevent high SAD. Two choices are left to us to achieve this goal:

Hence, we propose a sparse-refined term in the STE update formulation. We denote this new scheme as SR-STE. Compared to STE, when utilizing SR-STE in N:M sparse model training, the backward pass is carried out with a refined gradients for pruned weights, as illustrated in Fig. 2(b). The purpose of the regularization term is to decrease the magnitude of the pruned weights, which are determined in the forward pass. Intuitively, we encourage the pruned weights at the current iteration to be pruned also in the following iterations so that the sparse architecture is stabilized for enhancing the training efficiency and effectiveness.

Effects