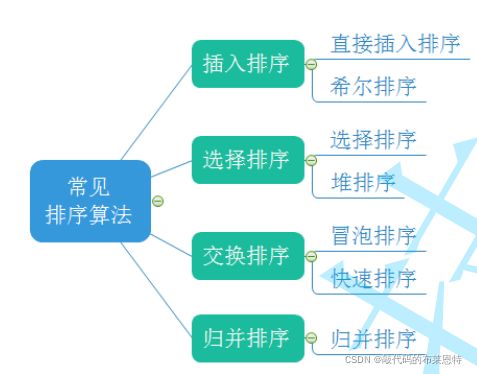
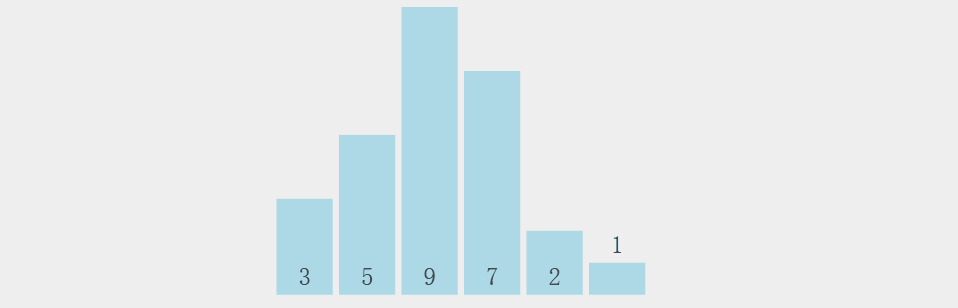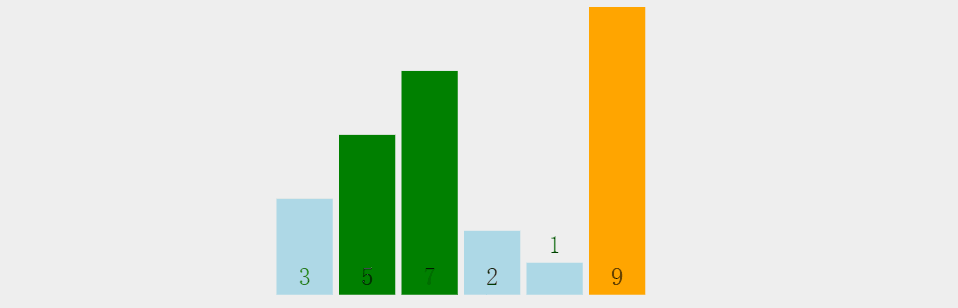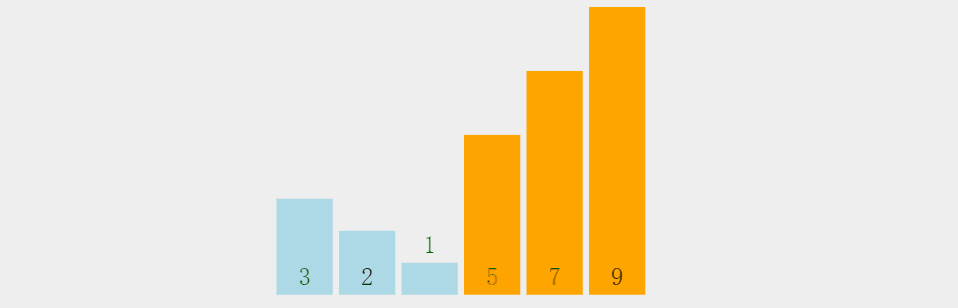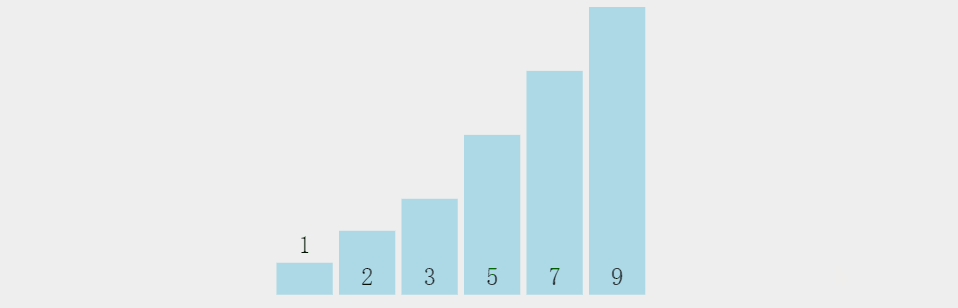【Java数据结构】想进大厂必须牢记于心的——常见八大排序算法
博客主页:敲代码的布莱恩特
欢迎点赞 收藏 ⭐留言 欢迎讨论!
本文由 【敲代码的布莱恩特】 原创,首发于 CSDN
由于博主是在学小白一枚,难免会有错误,有任何问题欢迎评论区留言指出,感激不尽!✨
精品专栏(不定时更新)【JavaSE】 【Java数据结构】【LeetCode】
【Java数据结构】想进大厂必须牢记于心的——常见八大排序算法
- 基本概念
-
- ⭐排序
- ⭐稳定性
- 七大基于比较的排序
-
- ⭐插入排序
-
- 1. 直接插入排序
- 2. 希尔排序(直接插入排序的优化)
- ⭐选择排序
-
- 3. 选择排序
- 4.堆排序(如果不了解堆的话可以看看我上一篇讲 堆 的博客)
- ⭐交换排序
-
- 5. 冒泡排序
- 6. 快速排序
- ⭐7. 归并排序·
- 非基于比较的排序
-
- 8. 基排序
- 总结
基本概念
⭐排序
- 排序,就是使一串记录,按照其中的某个或某些关键字的大小,
递增或递减的排列起来的操作。 - 平时的上下文中,如果提到排序,通常指的是排升序(非降序)。
- 通常意义上的排序,都是指的原地排序(in place sort)。
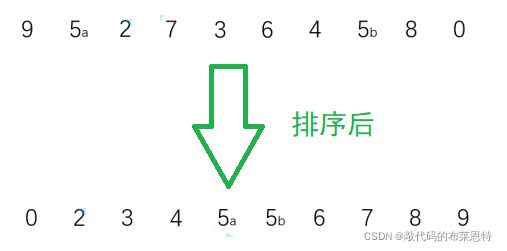
⭐稳定性
两个相等的数据,如果经过排序后,排序算法能 保证其相对位置不发生变化 ,则我们称该算法是具备 稳定性 的排序算法。
七大基于比较的排序
⭐插入排序
1. 直接插入排序
思路:
- 插入排序基本思想是将一个记录插入到已经排好序的有序表中,从而变成一个新的、记录数增1的有序表。
- 在其实现过程使用双层循环,外层循环对
除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动
图解:
代码实现:
/**
* 时间复杂度:
* 最好:O(N) -> 数据是有序的
*
* 最坏:O(N^2) -> 无序的数据
*
* 空间复杂度:O(1)
* 稳定性:稳定排序
* @param array
*/
//插入排序
public static void insertSort (int[]array){
for (int i = 1; i<array.length; i++){//外循环
//从1开始表示:假设array[0] 已经放好位置了
//后面的数字就是插入到它左边还是右边的问题。
int tmp = array[i];//设置一个缓存tmp
int j = i-1;
for (; j >=0 ; j--){//内循环
if (array[j]>tmp){//如果array[j]大于缓存值,说明要换位置
array[j+1] = array[j];
}else{//否则直接退出当前这一次的循环
break;
}
}
//最后记得要把缓存值插入到表中
array[j+1] = tmp;//j此时有可能已经是-1了,所以要变成0下标就得+1
}
}
2. 希尔排序(直接插入排序的优化)
思路:
- 希尔排序法又称缩小增量法。
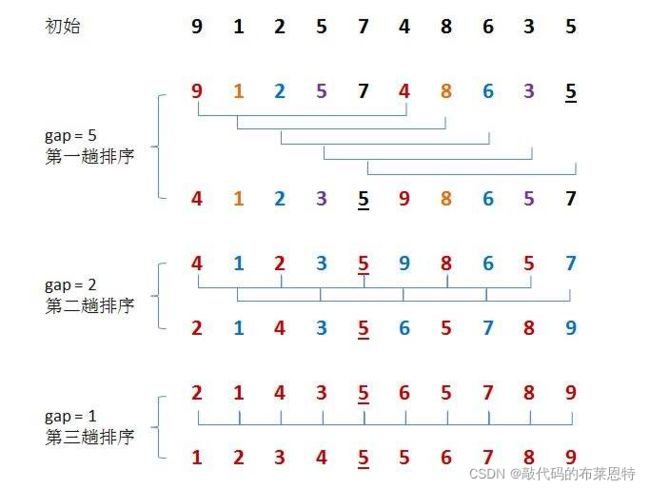
- 希尔排序法的基本思想是:
先选定一个整数(gap),把待排序文件中所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后,取gap / 2,重复上述分组和排序的工作。当gap到达1时,所有记录在同一组内排好序。 - 注意gap的问题:

- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。
当gap == 1时,数组已经接近有序的了,这时相当于直接用插入排序,这样就会很快,因为直接插入排序是越有序越快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
代码实现:
/**
* @param array 排序的数组
* @param gap 每组的间隔 -》 组数
*/
public static void shell(int[] array,int gap) {
//如果将gap全部换成1,会发现其实就是直接插入排序
//所以当gap到1的时候,这就表示这是最后一次排序
//这最后一次排序其实就是一个直接插入排序
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0; j -= gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}
/**
* 时间复杂度:不好算 n^1.3 - n^1.5 之间
* 空间复杂度:O(1)
* 稳定性:不稳定的排序
* 技巧:如果在比较的过程当中 没有发生跳跃式的交换 那么就是稳定的
* @param array
*/
public static void shellSort(int[] array) {
//处理gap
int gap = array.length;
while (gap > 1) {
gap /= 2;//保证最后一个序列间隔是 1 除几都行
shell(array,gap);
}
}
⭐选择排序
3. 选择排序
思路:
将一组数据分为有序区(排过序的数据)和无序区(未排序数据),每一次从无序区间选出最大(或最小)的一个元素,存放在无序区间的最后(或最前),直到全部待排序的数据元素排完 。
选择排序的步骤:
1>首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
2>再从剩余未排序元素中继续寻找最小(大)元素,然后放到未排序序列的起始位置。
3>重复第二步,直到所有元素均排序完毕。
图解:
代码实现:
/**
* 时间复杂度:
* 最好:O(N^2)
* 最坏:O(N^2)
* 空间复杂度:O(1)
* 稳定性:不稳定的
* @param array
*/
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {//下标i前边的为有序区间
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[i]) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
}
}
4.堆排序(如果不了解堆的话可以看看我上一篇讲 堆 的博客)
思路:
准备知识:
堆的结构可以分为大根堆和小根堆,是一个 完全二叉树,而堆排序是根据堆的这种数据结构设计的一种排序,下面先来看看什么是大根堆和小根堆
性质:
每个结点的值都大于其左孩子和右孩子结点的值,称之为大根堆;
每个结点的值都小于其左孩子和右孩子结点的值,称之为小根堆。
如下图
 我们对上面的图中每个数都进行了标记,上面的结构映射成数组就变成了下面这个样子
我们对上面的图中每个数都进行了标记,上面的结构映射成数组就变成了下面这个样子

基本步骤:
- 首先将待排序的数组构造成一个大根堆(升序用大根堆,降序就用小根堆),此时,
整个数组的最大值就是堆结构的顶端 - 将顶端的数与末尾的数交换,此时,末尾的数为最大值,将末尾这个最大值提取出去,剩余待排序数组个数为n-1
- 将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
图解:
代码实现:
//堆的向下调整
public static void siftDown(int[] array,int root,int len) {//len表示末尾元素下标
int parent = root;
int child = 2*parent+1;//先找到左孩子节点
while (child <= len) {//当child>length的时候说明当前子树已经调整好了
//先根据左孩子节点判断右孩子节点是否存在,且是否大于左孩子节点
if(child+1 <= len && array[child] < array[child+1]) {//如果存在,且值大于左孩子节点
child++;
}
//child的下标就是左右孩子的最大值下标
if(array[child] > array[parent]) {//如果孩子节点最大值,大于父节点,则要交换位置,因为要建大根堆
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
//继续向下看是否符合大根堆的条件
parent = child;//更新parent下标
child = 2*parent+1;//更新child下标
}else {//否则不用换位置
break;
}
}
}
//建堆
public static void createHeap(int[] array) {
//从小到大排序 -》 大根堆
for (int i = (array.length-1 - 1) / 2; i >= 0 ; i--) {
siftDown(array,i,array.length-1);
}
}
/**
* 时间复杂度:O(N*logN) 都是这个时间复杂度
* 复杂度:O(1)
* 稳定性:不稳定的排序
* @param array
*/
public static void heapSort(int[] array) {
createHeap(array);//O(n)
int end = array.length-1;//end表示当前末尾元素的下标
while (end > 0) {//O(N*logN)
int tmp = array[end];//因为要交换末尾与堆顶元素,所以先缓存末尾元素
//已经建好堆了,这时堆顶(0下标元素)就是当前的最大值
array[end] = array[0];//将他提取出来,放到数组的末尾,固定住
array[0] = tmp;//将末尾元素换到堆顶
end--;//固定了一个当前堆中的最大值之后,下一次参与排序的元素就得减少一个
siftDown(array,0,end);//将剩余元素继续变成一个大根堆
}
}
⭐交换排序
5. 冒泡排序
思路:
- 比较
相邻的两个元素。如果第一个比第二个大则交换他们的位置(升序排列,降序则反过来)。 - 从列表的开始一直到结尾,
依次对每一对相邻元素都进行比较。这样,值最大的元素就通过交换“冒泡”到了列表的结尾,完成第一轮“冒泡”。 - 重复上一步,继续从列表开头依次对相邻元素进行比较。已经“冒泡”出来的元素不用比较(一直比较到结尾也可以,已经“冒泡”到后面的元素即使比较也不需要交换,不比较可以减少步骤)。
- 继续从列表开始进行比较,
每轮比较会有一个元素“冒泡”成功。每轮需要比较的元素个数会递减,一直到只剩一个元素没有“冒泡”时(没有任何一对元素需要比较),则列表排序完成。
- 算法优化
如若在一轮排序中没有发生位置的交换,那么说明数据已经有序,不用继续进行后边的排序了
/**
* 时间复杂度:
* 最好最坏都是O(n^2) 但是:如果优化了 ,有序的时候就是O(n)
* 空间复杂度:O(1)
* 稳定性:稳定的排序
* 冒泡 直接插入
* @param array
*/
public static void bubbleSort(int[] array) {
for (int i = 0 ;i < array.length-1; i++){//外循环只用length-1趟
boolean flg = false;//记录当前这一趟是否有换位子
for (int j = 0 ; j <array.length-1-i ; j++){//内循环array.length-1-i趟
if (array[j] > array[j+1]){
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flg = true;
}
}
if (flg==false) {//如果当前趟没换位置,说明已经有序,不需要再排序了
break;
}
}
}
6. 快速排序
思路:
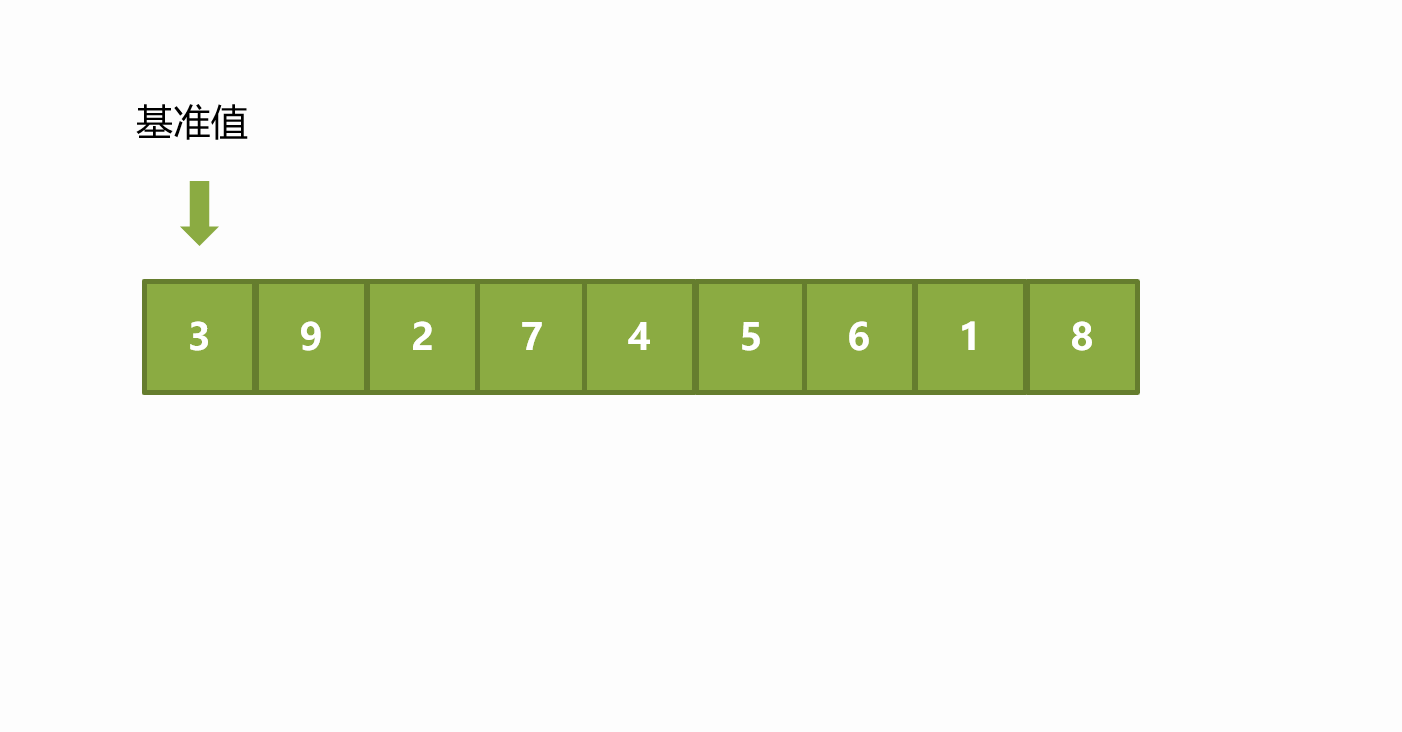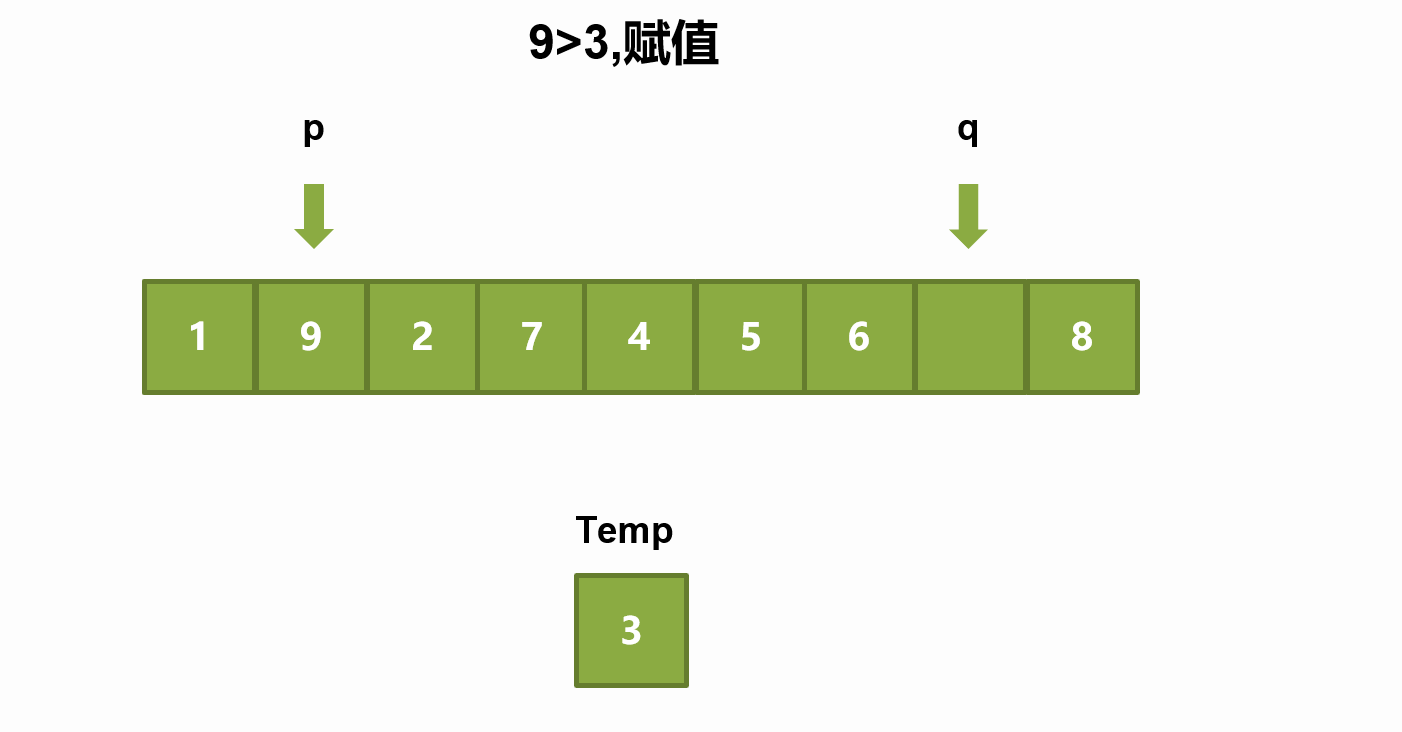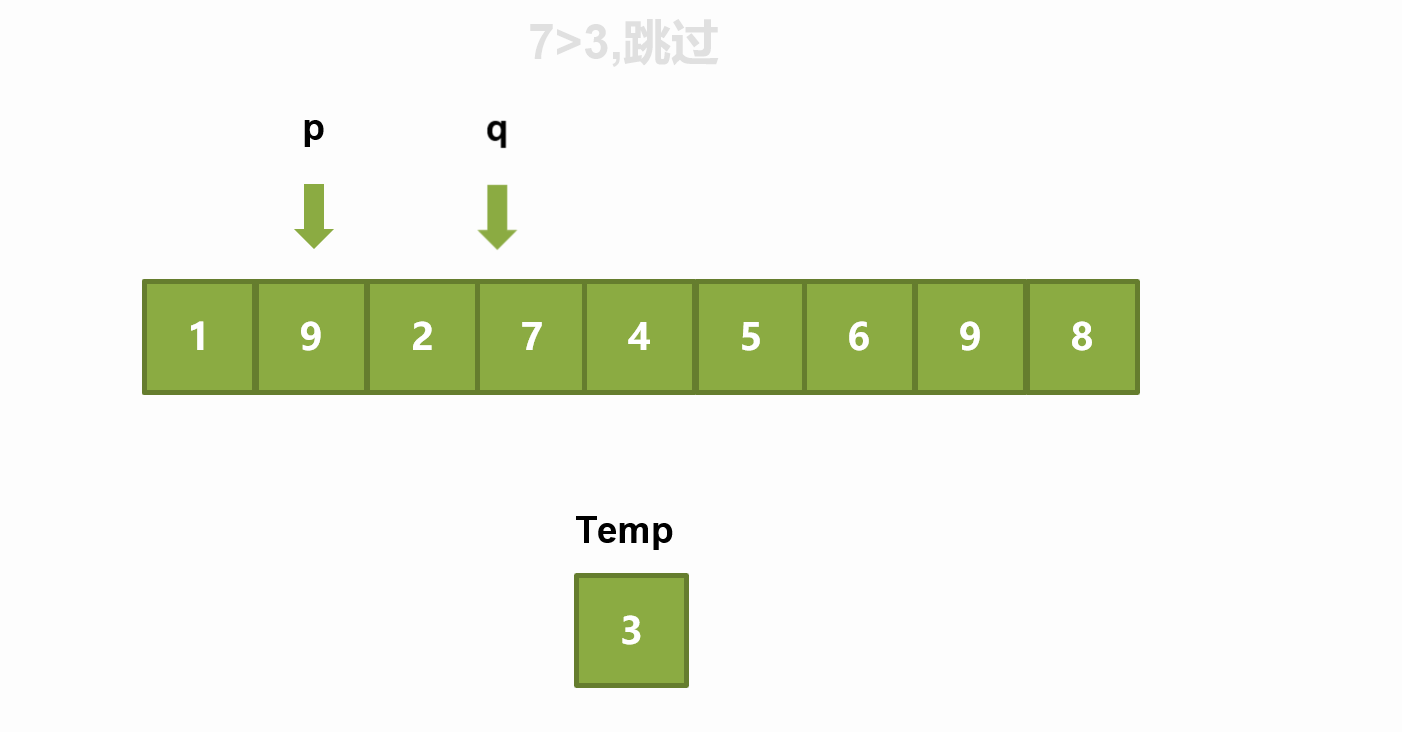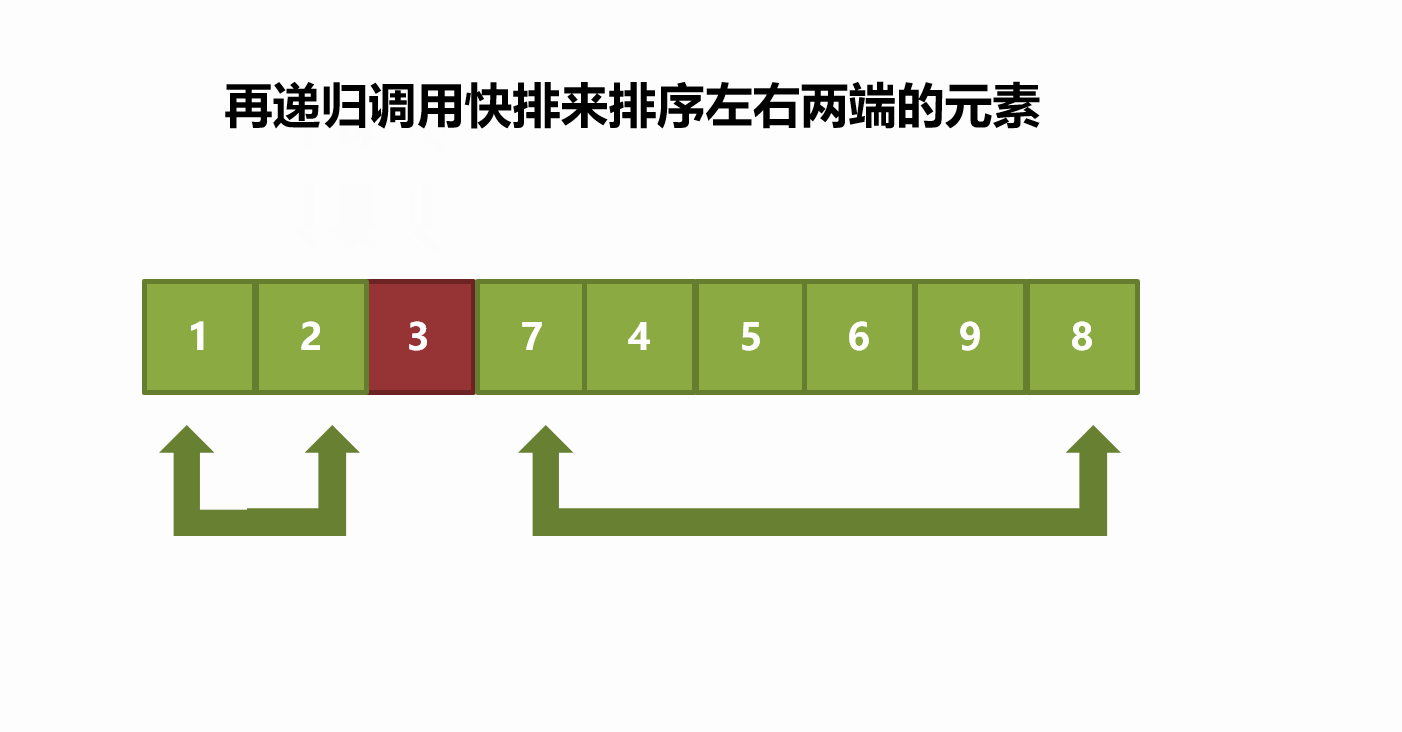
快速排序使用 分治策略 来把一个序列(list)分为两个子序列(sub-lists)。步骤为:
- 从数列中挑出一个元素,称为"
基准"(pivot)。
①选择边上(左或者右)默认用这种方式
②随机选择
③几数取中(例如三数取中):array[left], array[mid], array[right] 大小是中间的为基准值 - 重新排序数列(挖坑法),所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的
中间位置。这个称为分区(partition)操作。 - 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时,数列的大小是零或一,也就是已经排序好了。这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
代码实现:
/**
* 时间复杂度:
* 最好:O(n*logn) 均匀的分割下
* 最坏:o(n^2) 数据有序的时候
* 空间复杂度:
* 最好:logn
* 最坏:O(n)
* 稳定性:不稳定的排序
*
* k*n*logn
* 2
* 1.2
* @param array
*/
public static void quickSort(int[] array) {
sort(array, 0, array.length - 1);
}
private static void sort(int[] array, int low, int high) {
int i = low;
int j = high;
if (array.length <= 1) {
return;
}
if (i >= j) {
return;
}
int pivot = array[i];
//跳出while循环之后,因为循环的条件是i
while (i < j) {
//哨兵i从左往右找
while (i < j && array[j] >= pivot){
j--;
}
//哨兵j从右往左找
while (i < j && array[i] <= pivot){
i++;
}
//如果满足条件则交换两个数在数组中的位置
if (i<j) {//当哨兵i和哨兵j没有相遇时
int t = array[j];
array[j] = array[i];
array[i] = t;
}
}
//最终基准数归位
array[low] = array[i];//一开始low位置的数就是基准数
array[i] = pivot;//i下标值就是pivot基准值,由此可以递归左右两边的序列
sort(array, low, i - 1);//继续处理左边的,这里是递归的过程
sort(array, i + 1, high);//继续处理右边的,这里是递归的过程
}
非递归实现快速排序(重点掌握递归实现)
/**
* 非递归实现快速排序
* @param array
*/
public static void quickSort_FDG(int[] array) {
Stack<Integer> stack = new Stack<>();
int start = 0;
int end = array.length-1;
int pivot = partition(array,start,end);
//左边有2个元素及以上
if(pivot > start+1) {
stack.push(0);
stack.push(pivot-1);
}
if(pivot < end-1) {
stack.push(pivot+1);
stack.push(end);
}
while (!stack.empty()) {
end = stack.pop();
start = stack.pop();
pivot = partition(array,start,end);
//左边有2个元素及以上
if(pivot > start+1) {
stack.push(0);
stack.push(pivot-1);
}
if(pivot < end-1) {
stack.push(pivot+1);
stack.push(end);
}
}
}
⭐7. 归并排序·
思路:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
图解:
-
分而治之
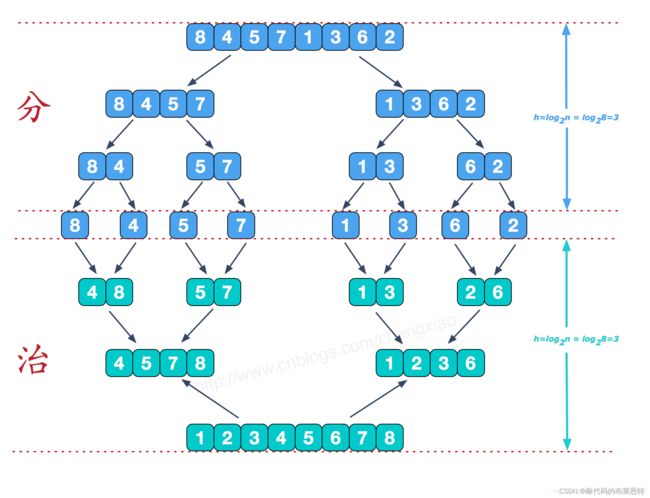
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。“分” 阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。 -
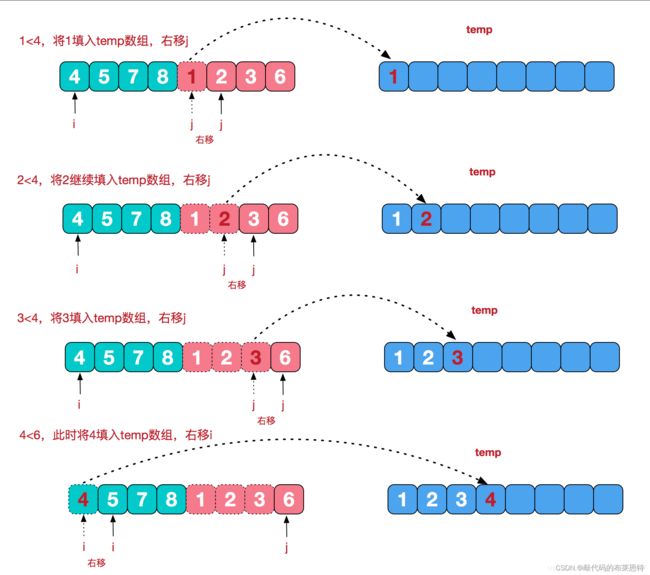
合并相邻有序子序列
再来看看 “治” 阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
代码实现:
public static void merge(int[] array,int low,int mid,int high) {
int s1 = low;
int e1 = mid;
int s2 = mid+1;
int e2 = high;
int[] tmp = new int[high-low+1];
int k = 0;//代表tmp数组的下标
while (s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
//k++;
//s1++;
}else {
tmp[k++] = array[s2++];
}
}
//有2种情况
while (s1 <= e1){
//说明第2个归并段没有了数据 把第1个归并段剩下的数据 全部拷贝过来
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
//说明第1个归并段没有了数据 把第2个归并段剩下的数据 全部拷贝过来
tmp[k++] = array[s2++];
}
//tmp数组当中 存储的就是当前归并好的数据,现在还需要拷贝到原数组中
//这样的代码是错误的
/*for (int i = 0; i < array.length; i++) {
array[i] = tmp[i];
}*/
for (int i = 0; i < tmp.length; i++) {
array[i+low] = tmp[i];//加上对应的low,用来处理第二个归并段,如果是第一个归并段,low=0
}
}
public static void mergeSortInternal(int[] array,int low,int high) {
if(low >= high) {
return;
}
int mid = (low+high) / 2;
mergeSortInternal(array,low,mid);//分解前半段
mergeSortInternal(array,mid+1,high);//分解后半段
//合并的过程
merge(array,low,mid,high);
}
/**
* 时间复杂度: O(N*log n)
* 空间复杂度:O(N)
* 稳定性:稳定的
* @param array
*/
public static void mergeSort(int[] array) {
mergeSortInternal(array, 0,array.length-1);
}
非递归实现归并排序(了解即可,重点掌握递归实现):
/**
* 非递归实现 归并排序
* @param array
* @param gap
*/
public static void merge2(int[] array,int gap) {
int[] tmp = new int[array.length];
int k = 0;
int s1 = 0;
int e1 = s1+gap-1;
int s2 = e1+1;
//int e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
int e2 = s2+gap-1 < array.length ? s2+gap-1 : array.length-1;
//保证有两个归并段
while (s2 < array.length) {
while (s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
while (s1 <= e1) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
//一组完了 确定新的区间的开始和结束
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2+gap-1 < array.length ? s2+gap-1 : array.length-1;
}
//e2 > array.length
while (s1 <= array.length-1) {
tmp[k++] = array[s1++];
}
for (int i = 0; i < tmp.length; i++) {
array[i] = tmp[i];
}
}
public static void mergeSort_FDG(int[] array) {
for (int i = 1; i < array.length; i*=2) {
merge2(array,i);
}
}
非基于比较的排序
8. 基排序
思路:
- 基数排序的思想就是先排好
个位,然后排好个位的基础上排十位,以此类推,直到遍历最高位 次,排序结束(仔细理解最后一句话) - 基数排序不是比较排序,而是通过分配和收集的过程来实现排序
初始化10个桶(固定的),桶下标为0-9- 通过得到待排序数字的个十百等位的数字,
把这个数字对应的item放到对应的桶中 - 基数排序有两种排序方式:LSD和MSD,最小位优先(从右边开始)和最大位优先(从左边开始)
图解:
代码实现:
public static void radixSort(int[] array) {
ArrayList<ArrayList<Integer>> queue = new ArrayList<>();
for (int i = 0; i <10 ; i++) {
queue.add(new ArrayList<>());// 创建一个基数从0---9 每个数字上都是一个list
}
// 找到最大值,并判断最大值是几位数
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (max < array[i]) {
max = array[i];
}
}
int time = 0;
while (max > 0) {
max /= 10;
time++;
}
for (int i = 0; i < time; i++) {// 循环每一个位数(个位、十位、百位)
for (int j = 0; j < array.length; j++) {// 循环数组,取每一个值
int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
ArrayList<Integer> queue3 = queue.get(x);
queue3.add(array[j]);
queue.set(x, queue3);
}
int count = 0;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList<Integer> queue4 = queue.get(k);
array[count] = queue4.get(0);
queue4.remove(0);
count++;
}
}
}
}
总结
一个稳定的排序,可以变成不稳定的排序
但是一个不稳定的排序,不可能变成稳定的排序

❤原创不易,如有错误,欢迎评论区留言指出,感激不尽❤
❤ 如果觉得内容不错,给个三连不过分吧~ ❤
❤ 看到会回访~ ❤