学习笔记10:统计学习方法:——HMM和CRF
文章目录
-
- 一、概率图模型
-
- 1.1 概览
- 1.2 有向图
- 1.3 无向图
- 1.4 生成式模型和判别式模型
- 1.4.1生成式模型和判别式模型区别
-
- 1.4.2 为啥判别式模型预测效果更好
- 二、隐式马尔科夫模型HMM
-
- 2.1 HMM定义
- 2.2 HMM三要素和两个基本假设
- 2.3 HMM三个基本问题
- 2.4 HMM基本解法
-
- 2.4.1 极大似然估计(根据I和O求λ)
- 2.4.2 前向后向算法(没有I)
- 2.4.3 序列标注(解码)过程
- 三、最大熵马尔科夫MEMM模型
-
- 3.1 MEMM原理和区别
- 3.2 标注偏置
- 四、条件随机场CRF
-
- 4.1 CRF定义
- 4.2 线性链CRF的计算
- 4.3 从公式到代码的理解
- 五、 HMM vs. MEMM vs. CRF
-
- 5.1 HMM vs MEMM
- 5.2 MEMM vs CRF
参考文章《如何用简单易懂的例子解释条件随机场(CRF)模型?它和HMM有什么区别?》
《条件随机场CRF之从公式到代码》
《CRF条件随机场的原理、例子、公式推导和应用》
一、概率图模型
1.1 概览
在统计概率图(probability graph models)中,参考宗成庆老师的书,是这样的体系结构:

在概率图模型中,数据(样本)由图 G = ( V , E ) G=(V,E) G=(V,E)建模表示:
- V:节点v的集合。v∈V表示随机变量 Y v Y_v Yv。
- E:边e的集合。e∈E表示随机变量之间的概率依赖关系。
- P(Y):由图表示的联合概率分布
有向图和无向图区别在于如何求概率分布P(Y)。
1.2 有向图
有向图模型,这么求联合概率:
P ( x 1 . . . x n ) = ∏ i = 0 P ( x i ∣ π ( x i ) ) P(x_{1}...x_{n})=\prod_{i=0}P(x_{i}|\pi (x_{i})) P(x1...xn)=i=0∏P(xi∣π(xi))
对于下图求概率有:
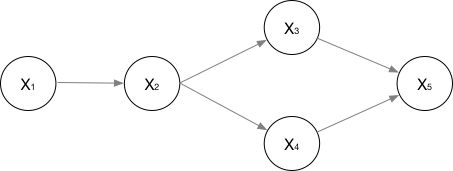
P ( x 1 . . . x n ) = P ( x 1 ) ⋅ P ( x 2 ∣ x 1 ) ⋅ P ( x 3 ∣ x 2 ) ⋅ P ( x 4 ) ∣ P ( x 2 ) P ( x 5 ∣ x 3 , x 4 ) P(x_{1}...x_{n})=P(x_{1})\cdot P(x_{2}| x_{1})\cdot P(x_{3}| x_{2})\cdot P(x_{4})|P(x_{2})P(x_{5}|x_{3},x_{4}) P(x1...xn)=P(x1)⋅P(x2∣x1)⋅P(x3∣x2)⋅P(x4)∣P(x2)P(x5∣x3,x4)
1.3 无向图
基本概念:
- 团:节点子集,子集中任何两个节点均有边相连
- 最大团:不能再加入节点使其更大的团
- 因子分解:联合概率分布P(Y)表示为
所有最大团上随机变量函数的乘积的形式为因子分解。
所以有:联合概率分布为最大团势函数的乘积。
P ( Y ) = 1 Z ∏ C ψ C ( Y C ) = 1 Z ∏ C e x p − E ( Y C ) P(Y)=\frac{1}{Z}\prod_{C}\psi _{C}(Y_{C})=\frac{1}{Z}\prod_{C}exp^{-E(Y_{C})} P(Y)=Z1C∏ψC(YC)=Z1C∏exp−E(YC)
- C:无向图的最大团
- Y C Y_{C} YC:最大团C上的节点(随机变量)
- Z:规范化因子。 Z = ∑ Y ∏ C ψ C ( Y C ) Z=\sum_{Y}\prod_{C}\psi _{C}(Y_{C}) Z=∑Y∏CψC(YC),使得输出P(Y)具有概率意义。
- ψ C ( Y C ) \psi _{C}(Y_{C}) ψC(YC):严格正的势函数,通常为指数函数 ψ C ( Y C ) = e x p − E ( Y C ) \psi _{C}(Y_{C})=exp^{-E(Y_{C})} ψC(YC)=exp−E(YC)。
马尔科夫性,保证概率图为概率无向图:
- 成对马尔科夫性:u和v没有边相连,O为其它所有节点, Y u 和 Y v Y_u和Y_v Yu和Yv互相独立。
- 局部马尔科夫性:对于任意节点v、相连节点集合W和无边相连集合O,给定 Y W Y_W YW情况下, Y v 和 Y O Y_v和Y_O Yv和YO互相独立:
- 全局马尔科夫性:节点A和B被节点集合C分割, Y A 和 Y B Y_A和Y_B YA和YB互相独立:
总之就是没有边相连的节点概率互相独立。
对于一个无向图,举例如下:
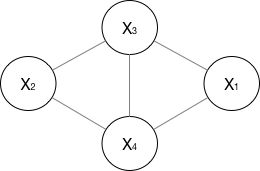
P ( Y ) = 1 Z ∏ C ψ ( X 1 , X 3 , X 4 ) ψ ( X 2 , X 3 , X 4 ) P(Y)=\frac{1}{Z}\prod_{C}\psi( _{X_{1},X_{3},X_{4}})\psi( _{X_{2},X_{3},X_{4}}) P(Y)=Z1C∏ψ(X1,X3,X4)ψ(X2,X3,X4)
1.4 生成式模型和判别式模型
1.4.1生成式模型和判别式模型区别
有监督学习中,训练数据包括输入X和标签Y。所以模型求的是X和Y的概率分布。根据概率论的知识可以知道,对应的概率分布(以概率密度函数指代概率分布)有两种:
- 联合概率分布: P θ ( X , Y ) P_{\theta }(X,Y) Pθ(X,Y),表示数据和标签同时出现的概率,对应于生成式模型。
- 条件概率分布:P_{\theta }(Y|X),表示给定数据条件下,对应标签的概率,对应于判别式模型。
进一步理解:
- 生成式模型:除了能够根据输入数据 X 来预测对应的标签 Y ,还能根据训练得到的模型产生服从训练数据集分布的数据( X ,Y),相当于生成一组新的数据,所以称之为生成式模型。
- 判别式模型:仅仅根据X由条件概率 P θ ( Y ∣ X ) P_{\theta }(Y|X) Pθ(Y∣X)来预测标签Y。牺牲了生成数据的能力,但是比生成式模型的预测准确率高。
1.4.2 为啥判别式模型预测效果更好
原因如下:由全概率公式和信息熵公式可以得到:
P ( X , Y ) = ∫ P ( Y ∣ X ) P ( X ) d X P(X,Y)=\int P(Y|X)P(X)dX P(X,Y)=∫P(Y∣X)P(X)dX
即计算全概率公式 P ( X , Y ) P(X,Y) P(X,Y)时引入了输入数据的概率分布 P ( X ) P(X) P(X),而这个并不是我们关心的。我们只关心给定X情况下Y的分布,这就相对削弱了模型的预测能力。
另外从信息熵的角度进行定量分析。
- X的信息熵定义为:
H ( X ) = − ∫ P ( X ) l o g P ( X ) d X H(X)=-\int P(X)logP(X)dX H(X)=−∫P(X)logP(X)dX - 两个离散随机变量 X 和 Y 的联合熵 (Joint Entropy) 表示两事件同时发生系统的不确定度:
H ( X , Y ) = − ∫ P ( X , Y ) l o g P ( X , Y ) d X d Y H(X,Y)=-\int P(X,Y)logP(X,Y)dXdY H(X,Y)=−∫P(X,Y)logP(X,Y)dXdY - 条件熵 (Conditional Entropy) H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性:
H ( Y ∣ X ) = − ∫ P ( Y ∣ X ) l o g P ( Y ∣ X ) d X H(Y|X)=-\int P(Y|X)logP(Y|X)dX H(Y∣X)=−∫P(Y∣X)logP(Y∣X)dX
可以推导出来 H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X).一般H(X)>0(所有离散分布和很多连续分布满足这个条件),可以知道条件分布的信息熵小于联合分布,即判别模型比生成式模型含有更多的信息,所以同条件下比生成式模型效果更好。
二、隐式马尔科夫模型HMM
2.1 HMM定义
- 隐马尔可夫模型是关于时序的概率模型
- 描述由一个
隐藏的马尔可夫链随机生成不可观测的状态随机序列(state sequence),再由各个状态生成一个观测而产生观测随机序列(observation sequence )的过程,序列的每一个位置又可以看作是一个时刻。
设Q是所有可能状态的集合,V是所有可能观测的集合:
Q = ( q 1 , q 2 , . . . q N ) 和 V = ( v 1 , v 2 , . . . v M ) Q=(q_{1},q_{2},...q_{N})和V=(v_{1},v_{2},...v_{M}) Q=(q1,q2,...qN)和V=(v1,v2,...vM)
对于长度为T的状态序列I和观测序列O有:
i = ( i 1 , i 2 , . . . i T ) 和 O = ( o 1 , o 2 , . . . o T ) i=(i_{1},i_{2},...i_{T})和O=(o_{1},o_{2},...o_{T}) i=(i1,i2,...iT)和O=(o1,o2,...oT)
其中:
- 状态转移概率矩阵 A = ( a i j ) N × N i , j ϵ ( 1 , N ) A=(a_{ij})_{N\times N}\qquad i,j\epsilon (1,N) A=(aij)N×Ni,jϵ(1,N)。 a i j a_{ij} aij表示t时刻状态 q i q_i qi转移到t+1时刻 q j q_j qj的概率
- 观测概率(发射概率)矩阵 B = [ b j ( k ) ] N × M j ϵ ( 1 , N ) k ϵ ( 1 , M ) B=[b_{j}(k)]_{N\times M} \quad j\epsilon (1,N)k\epsilon (1,M) B=[bj(k)]N×Mjϵ(1,N)kϵ(1,M)。 b j ( k ) b_{j}(k) bj(k)表示t时刻状态 q i q_i qi生成观测 v k v_k vk的概率。
- 初始状态概率向量 π = ( π i ) = P ( i 1 = q i ) i ϵ ( 1 , N ) \pi =(\pi _{i})=P(i_{1}=q_{i})\quad i\epsilon (1,N) π=(πi)=P(i1=qi)iϵ(1,N)。表示初始时刻处于状态 q i q_i qi的概率。

- 隐状态节点 i t i_t it在A的指导下生成下一个隐状态节点 i t + 1 i_{t+1} it+1,并且 i t i_t it在B的指导下生成观测节点 o t o_t ot , 并且我只能观测到序列O。
- 根据概率图分类,可以看到HMM属于有向图,并且是生成式模型,直接对联合概率分布建模:

只是我们都去这么来表示HMM是个生成式模型,实际不这么计算。
2.2 HMM三要素和两个基本假设
- HMM由
初始状态概率向量π、状态转移概率矩阵A、 观测概率矩阵B三元素构成。
所以HMM模型 λ \lambda λ可以写成: λ = ( A , B , π ) \lambda =(A,B,\pi) λ=(A,B,π)。三者共同决定了隐藏的马尔可夫链生成不可观测的状态序列。而状态序列和矩阵B综合产生观测序列。 - HMM模型基本假设
- 齐次马尔科夫性假设:隐马尔可夫链任意时刻t的状态只依赖前一时刻t-1的状态,即 P ( i t ∣ i i − 1 ) P(i_{t}|i_{i-1}) P(it∣ii−1)。
- 观测独立性假设:任意时刻的观测只依赖当前时刻的状态,即 P ( o t ∣ i i ) P(o_{t}|i_{i}) P(ot∣ii)。
2.3 HMM三个基本问题
- 概率计算:给定模型 λ = ( A , B , π ) \lambda =(A,B,\pi) λ=(A,B,π)和观测序列O,计算观测序列O出现的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)。
- 学习问题:已知观测序列O,用最大似然估计的方法计算模型 λ = ( A , B , π ) \lambda =(A,B,\pi) λ=(A,B,π)的参数。(该模型下观测序列O的概率最大)
- 预测(解码)问题:已知模型 λ = ( A , B , π ) \lambda =(A,B,\pi) λ=(A,B,π)和观测序列,求最有可能的对应状态序列。
- HMM可以用于序列标记,观测序列O为tokens,状态序列I为其对应的标记。此时问题是给定序列O预测对应序列I。
- 问题2对应模型建立过程,问题3 对应解码过程(crf.decode)
2.4 HMM基本解法
2.4.1 极大似然估计(根据I和O求λ)
一般做NLP的序列标注等任务,在训练阶段肯定是有隐状态序列的,即根据观测序列O和状态序列I求模型 λ = ( A , B , π ) \lambda =(A,B,\pi) λ=(A,B,π)的参数,是一个有监督学习。
- 根据状态序列求状态转移矩阵A:
a i j = A i j ∑ j = 1 N A i j \mathbf{a_{ij}=\frac{A_{ij}}{\sum_{j=1}^{N}A_{ij}}} aij=∑j=1NAijAij - 根据状态序列I和观测序列O求观测概率矩阵B:
b j ( k ) = B j k ∑ k = 1 M B j k \mathbf{b_{j}(k)=\frac{B_{jk}}{\sum_{k=1}^{M}B_{jk}}} bj(k)=∑k=1MBjkBjk - 直接估计π
2.4.2 前向后向算法(没有I)
只有观测序列O,没有状态序列I,无监督过程。计算就是一个就EM的过程。

2.4.3 序列标注(解码)过程
- 学习完了HMM的分布参数,也就确定了一个HMM模型。序列标注问题也就是“预测过程”(解码过程)。对应了序列建模问题3。
- 学习后已知了 联合概率P(I,O),现在要求出条件概率P(I|O):
I m a x = a r g m a x a l l I P ( I , O ) P ( O ) I_{max}=\underset{all I}{argmax}\frac{P(I,O)}{P(O)} Imax=allIargmaxP(O)P(I,O) - 用Viterbi算法解码,在给定的观测序列下找出一条概率最大的隐状态序列。
- Viterbi计算有向无环图的一条最大路径,用DP思想减少重复的计算。如图:

三、最大熵马尔科夫MEMM模型
3.1 MEMM原理和区别
MEMM是判别式模型,直接对条件概率建模:
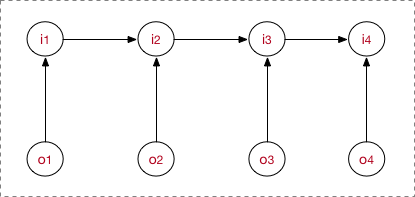
MEMM需要注意:
-
HMM是 o t o_t ot只依赖当前时刻的隐藏状态 i t i_t it,HEMM是当前时刻隐状态 i t i_t it依赖观测节点 o t o_t ot和上一时刻状态 i t − 1 i_{t-1} it−1。
-
判别式模型是用函数直接判别,学习边界,MEMM即通过特征函数来界定。HMM是生成式模型,参数即为各种概率分布元参数,数据量足够可以用最大似然估计。但同样,MEMM也有极大似然估计方法、梯度下降、牛顿迭代发、拟牛顿下降、BFGS、L-BFGS等等 -
需要注意,之所以图的箭头这么画,是由MEMM的公式决定的,而公式是creator定义出来的。
-
序列标注解码时,一样用维特比算法求概率最大的隐状态序列。
- HMM中,观测节点 o t o_t ot只依赖当前时刻的隐藏状态 i t i_t it。
- 更多的实际场景下,观测序列是需要很多的特征来刻画的。比如说,我在做NER时,我的标注 i t i_t it不仅跟当前状态 o t o_t ot相关,而且还跟前后标注 i j ( j ≠ i ) i_{j}(j≠i) ij(j=i)相关,比如字母大小写、词性等等。
- MEMM模型:允许“定义特征”,直接学习条件概率,即:

- Z ( o , i ′ ) Z(o,i{}') Z(o,i′):归一化系数
- f ( o , i ) f(o,i) f(o,i):特征函数,需要自定义,其个数可任意制定
- λ:特征函数系数,需要训练得到

3.2 标注偏置
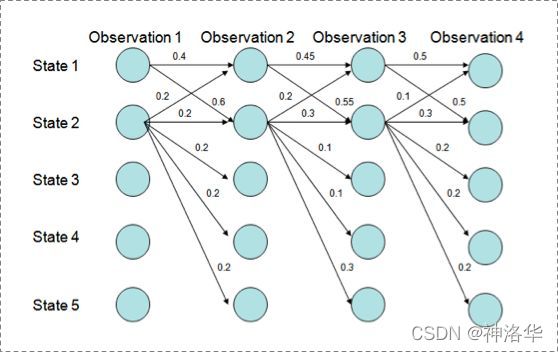
用Viterbi算法解码MEMM,状态1倾向于转换到状态2,同时状态2倾向于保留在状态2。 过程细节:
P(1-> 1-> 1-> 1)= 0.4 x 0.45 x 0.5 = 0.09 ,
P(2->2->2->2)= 0.2 X 0.3 X 0.3 = 0.018,
P(1->2->1->2)= 0.6 X 0.2 X 0.5 = 0.06,
P(1->1->2->2)= 0.4 X 0.55 X 0.3 = 0.066
但是得到的最优的状态转换路径是1->1->1->1,
为什么呢?因为状态2可以转换的状态比状态1要多,从而使转移概率降低,即MEMM倾向于选择拥有更少转移的状态。原因如下:
四、条件随机场CRF
4.1 CRF定义
-
条件随机场:给定随机变量X条件下,输出随机变量Y的条件概率模型,其中Y构成无向图G=(V,E)表示的马尔科夫随机场。
对任意节点v,条件随机场满足:
P ( Y v ∣ X , Y w , w ≠ v ) = P ( Y v ∣ X , Y w , w ∼ v ) P(Y_{v}|X,Y_{w},w\neq v)=P(Y_{v}|X,Y_{w},w\sim v) P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w∼v)
w≠ v表示v之外的所有结点,w~v表示与v有边相连的所有结点。即 P ( Y v P(Y_{v} P(Yv之和与v有边连接的结点有关。 -
线性链条件随机场,最大团是相邻两个结点的集合。满足马尔科夫性(隐状态只和前后时刻状态有关):
P ( Y i ∣ X , Y 1 , Y 2 . . . Y n ) = P ( Y i ∣ X , Y i + 1 , Y i − 1 ) P(Y_{i}|X,Y_{1},Y_{2}...Y_{n})=P(Y_{i}|X,Y_{i+1},Y_{i-1}) P(Yi∣X,Y1,Y2...Yn)=P(Yi∣X,Yi+1,Yi−1) -
线性链CRF是判别模型,学习方法是利用训练数据的(正则化)极大似然估计得到条件概率模型P(Y|X)。可用于序列标注问题。此时条件概率P(Y|X)中:
- Y为输出变量,即标记序列(状态序列)
- X为输入变量,即需要标注的状态序列。
4.2 线性链CRF的计算
- 下标i表示我当前所在的节点(token)位置。
- 下标k表示我这是第几个特征函数,并且每个特征函数都附属一个权重 λ k \lambda_{k} λk 。即每个团里面,我将为 t o k e n i token_i tokeni构造M个特征,每个特征执行一定的限定作用,然后建模时我再为每个特征函数加权求和。
- Z(O)是用来归一化的,形成概率值。
- P ( I ∣ O ) P(I|O) P(I∣O)表示了在给定的一条观测序列 O的条件下,我用CRF所求出来的隐状态序列 I = ( i 1 , i 2 , . . . i T ) I=(i_{1},i_{2},...i_{T}) I=(i1,i2,...iT)的概率。而至于观测序列 O,它可以是一整个训练语料的所有的观测序列;也可以是在推断阶段的一句sample。比如序列标注进行预测,最终选的是最大概率的那条(by viterbi)。
- 对于CRF,可以为他定义两款特征函数:转移特征&状态特征。 我们将建模总公式展开:
为了简单起见,将转移特征和状态特征及其权值用统一符号表示。条件随机场简化公式如下:
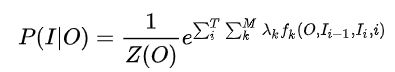
再进一步理解的话,我们需要把特征函数部分抠出来:
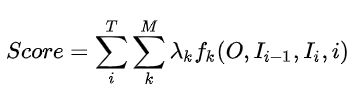
我们为 t o k e n i token_i tokeni打分,满足条件的就有所贡献。最后将所得的分数进行log线性表示,求和后归一化,即可得到概率值。
具体应用求解参考《如何用简单易懂的例子解释条件随机场(CRF)模型?它和HMM有什么区别?》。
4.3 从公式到代码的理解
实际计算时,采用概率的对数形式,即logP(Y)。使用最大似然估计来计算分布的参数,即我们的目标就是最大化ogP(Y)。

即 − l o g P ( Y ) = l o g Z ( x ) − s c o r e -logP(Y)=logZ(x)-score −logP(Y)=logZ(x)−score。
对应到代码中,forward_score 就是 l o g Z ( x ) logZ(x) logZ(x),gold_score就是特征函数部分的score。
def neg_log_likelihood(self, sentence, tags):
feats = self._get_lstm_features(sentence)
forward_score = self._forward_alg(feats)
gold_score = self._score_sentence(feats, tags)
return forward_score - gold_score
- 因为模型建立的初衷就是要考虑到 i k − 1 i_{k-1} ik−1对 i k i_{k} ik的影响和X对观测序列的影响.所以我们将图分解成若干个 ( i k − 1 , i k , X ) (i_{k-1},i_{k},X) (ik−1,ik,X)。
- 其中 i k i_{k} ik表示观测变量的状态值,比如在BIO标注中状态取值范围是{B,I,O,START,STOP},则k最大取5, i k i_{k} ik有5个状态值可取。

只关注其中的某一个团 C i C_i Ci,特征函数部分的gold_score表示给定序列X下,表现出的 ( i k − 1 , i k ) (i_{k-1},i_{k}) (ik−1,ik)的费归一化概率,与两个东西有关:
- 给定序列X下出现 i k i_{k} ik的概率,以 h ( i k , X ) h(i_{k},X) h(ik,X)表示。这个概率使用lstm、cnn建模X对 i k ) i_{k}) ik)映射就可以得到,对应结点上的状态特征。
- 给定序列X下由 i k − 1 i_{k-1} ik−1转移到 i k i_{k} ik的概率,由 g ( i k − 1 , i k ; X ) g(i_{k-1},i_{k};X) g(ik−1,ik;X)表示,对应边上的转移特征。在CRF中,观测变量只受临近节点的影响。
- 考虑到深度学习模型已经能比较充分捕捉各个 i k i_{k} ik与X 的联系,所以假设 i k − 1 i_{k-1} ik−1 转移到 i k i_{k} ik的概率与X无关,所以有: g ( i k − 1 , i k ; X ) = g ( i k − 1 , i k ) g(i_{k-1},i_{k};X)=g(i_{k-1},i_{k}) g(ik−1,ik;X)=g(ik−1,ik)
考虑以上几点,可以得到:
g o l d − s c o r e = ∑ c ∑ k λ k f k ( c , y , x ) = ∑ c ∑ k ( g ( i k − 1 , i k ) + h ( i k , X ) ) gold-score=\sum_{c}\sum_{k}\lambda _{k}f_{k}(c,y,x)=\sum_{c}\sum_{k}(g(i_{k-1},i_{k})+h(i_{k},X)) gold−score=c∑k∑λkfk(c,y,x)=c∑k∑(g(ik−1,ik)+h(ik,X))
五、 HMM vs. MEMM vs. CRF
5.1 HMM vs MEMM
HMM模型中存在两个假设:一是输出观察值之间严格独立,二是状态的转移过程中当前状态只与前一状态有关。但实际上序列标注问题不仅和单个词相关,而且和观察序列的长度,单词的上下文,等等相关。MEMM解决了HMM输出独立性假设的问题。因为HMM只限定在了观测与状态之间的依赖,而MEMM引入自定义特征函数,不仅可以表达观测之间的依赖,还可表示当前观测与前后多个状态之间的复杂依赖。
5.2 MEMM vs CRF
CRF不仅解决了HMM输出独立性假设的问题,还解决了MEMM的标注偏置问题,MEMM容易陷入局部最优是因为只在局部做归一化,而CRF统计了全局概率,在做归一化时考虑了数据在全局的分布,而不是仅仅在局部归一化,这样就解决了MEMM中的标记偏置的问题。使得序列标注的解码变得最优解。HMM、MEMM属于有向图,所以考虑了x与y的影响,但没将x当做整体考虑进去(这点问题应该只有HMM)。CRF属于无向图,没有这种依赖性,克服此问题。