k近邻算法实现--Knn
目录
- 算法原理
- 算法优缺点
-
- 算法变种
- sklearn.KNeighborsClassifier
-
- 重要参数
-
- n_neighbors
- weights
- algorithm
- 类方法
-
- fit(x,y)
- keighbors()
-
- 重要参数
-
- x
- n_neighbors
- return_distance
- 返回值
- predict(x)
- 使用knn进行分类的例子
- sklearn.KNeighborsRegressor
-
- 使用knn进行回归拟合的例子
本博客参考书籍:scikit-learn机器学习–常用算法原理及编程实战
算法原理
一种有监督的机器学习算法,常用于解决分类和回归问题
**核心思想:**一个为被标记的样本类别由距离其最近的k个邻居决定
使用一个已经标记的数据样本进行训练,即拟合数据与标签
计算待标记的数据样本的数据集中每个样本的距离,取距离最近的k个样本,观察这K个样本所属的类别,样本最多的那个类别即为待标记数据所属于的类别
算法优缺点
| 优点 | 准确性高,异常值和噪声对结果影响相对较小 |
| 缺点 | 对内存需求较大,每对一个样本进行分类都需要将距离全部计算一遍 |
算法变种
Knn算法的一个变种是增加邻居点的权重,我们可以给距离样本点不同距离的样本点指定不同的权重,距离越近权重越高,这个算法变种可以通过KNeighborsClassifier类中的weight参数指定
sklearn.KNeighborsClassifier
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
重要参数
n_neighbors
参与评价样本点分类的邻居个数 。
值越大,决定其类别的邻居越多,模型的偏差也会越大,对噪声数据也会变得不敏感;值过大可能会造成模型欠拟合,值过小会造成相反的效果
weights
| 可能取值 | 描述 |
|---|---|
| uniform | 平均权重,距离样本点不同的邻居具有相同的权重 |
| distance | 权重取决于邻居距离样本点的距离 |
| [callable] | 自定义权重分配方法 |
algorithm
用于计算最近邻居的算法
| 可能取值 | 描述 |
|---|---|
| ‘ball_tree’ | BallTree算法 |
| ‘kd_tree’ | KDTree算法 |
| ‘brute’ | 强力搜索 |
| ‘auto’ | 尝试根据数据寻找最合适的分类算法传递给fit() |
类方法
fit(x,y)
使用训练数据集拟合k近邻分类器
x,y分别表示训练数据及其对应的标签
keighbors()
keighbors([X, n_neighbors, return_distance])
寻找样本点的k个最近邻居
重要参数
x
array-like
需要查询的点(一个或多个)
n_neighbors
int,None
邻居个数,默认值为模型中的n_neighbors
return_distance
bool,True
是否返回每个邻居距离样本点的距离
返回值
距离样本点最近的邻居们距离样本点的距离(当return_distance为True时返回),数据类型:ndarray of (x.shape,n_neighbors)
距离样本点最近的邻居们在原训练数据集中的索引数据类型:ndarray of (x.shape,n_neighbors)
实例:
predict(x)
对样本x进行预测
使用knn进行分类的例子
生成一个包含50个样本点(3个种群)的数据集作为训练数据,使用该数据集对knn模型进行拟合,然后使用拟合后的模型队训练数据进行预测
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
x,y=make_blobs(n_samples=50,cluster_std=0.6)
clf=KNeighborsClassifier(n_neighbors=2)
clf.fit(x,y)
x_sample=[[2,-2],[0,0],[3,0]] # 待分类的样本点
y_sample=clf.predict(x_sample) # 使用拟合过的knn模型进行预测
y_sample
>>> array([0, 1, 1])
neighbors=clf.kneighbors(x_sample) # 查看距离样本点最近的邻居信息
>>> (array([[3.81072592, 3.87193455],
[1.81365177, 1.85249566],
[2.49118958, 2.56258328]]),
array([[45, 5],
[44, 35],
[19, 5]], dtype=int64))
'''上面的第一个array数组中的元素分别表示距离(3个)样本点距离最近的2个邻居的距离
第二个array数组中的元素分别表示距离(3个)样本点距离最近的2个样本点在原训练数据即中的索引
'''
sklearn.KNeighborsRegressor
分类问题的预测值是离散的,下面使用KNN算法在连续区间内对数值进行预测,即回归拟合
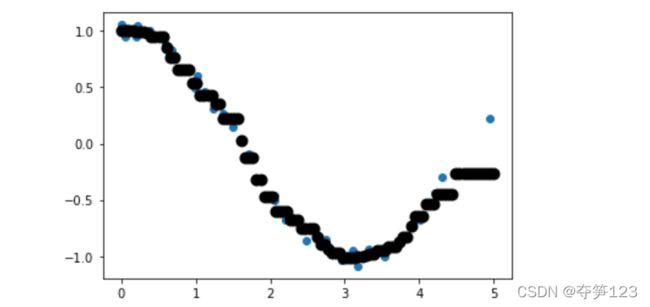
使用knn进行回归拟合的例子
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsRegressor
x=5*np.random.rand(40,1) # 生成训练数据集
y=np.cos(x).ravel() # ravel()方法将y的维度由(40,1)转化为(40,)
knn=KNeighborsRegressor(5)
knn.fit(x,y)
x_sample=np.linspace(0,5,100).reshape(-1,1) # 生成测试数据
y_sample=knn.predict(x_sample) # 使用knn回归拟合
plt.figure()
plt.scatter(x,y)
plt.scatter(x_sample,y_sample,c='k',lw=4)
plt.show()