浅谈估值模型 (二): 相对估值模型中的变形金刚——PE指标I
1：本文主要讨论将PE指标进行平滑改造(附完整源代码)；
2：本文主要为理念的讲解，模型也是笔者自建；
3：本文主要数据均通过Tushare(ID：444829)金融大数据平台接口获取；
4：笔者希望搭建出一套交易体系，原则是只做干货的分享。后续将更新更多模块，但工作学习之余的闲暇时间有限，更新速度慢还请谅解；
5：文中假设与观点是基于笔者对模型及数据的一孔之见，若有不同见解欢迎随时留言交流；
6：模型实现基于python3.8；
目录
1. 浅谈PE
2. 相对vs绝对
3. PE指标里的不合理因素
3.1 EPS拆解
3.2 EPS分析
3.3 EPS平滑方式
3.4 EPS平滑
4. 根据平滑后的EPS计算新的PE指标
5. 整合代码
6. 写在后面
1. 浅谈PE
PE指标的一些解释，不感兴趣的读者可以直接跳转第三部分看正文。
PE指标作为投资决策中的Super爱豆(超级大明星)， 被各路人马用到烂。 戴维斯1950年买入4倍PE的保险股，10年后在18倍PE抛出，于是有了大名鼎鼎的戴维斯双击；彼得·林奇眼中的PE被增长率所调整，于是有了PEG；自从PE被发明出来便是风靡，可以说上到股神，下到散户无人不知无人不晓。只怕从大A股里随便挑出个散户都能拿出炒股软件把个股的PE分析得头头是道。
但PE远远不止我们能在看盘软件上看到的静态PE，动态PE， PE(TTM)那么简单。 在笔者看来它是相对估值下变形最多，最为复杂的一个指标，看似简单，实则内中玄机非一般人能窥， 不然同样都是用PE的，凭什么彼得林奇，戴维斯，巴菲特用了就是大师，A股散户用了就是韭菜？
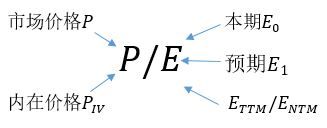
在用PE的时候首先要明确1)：P是哪个P？ 既可以采用目前市场上能观测到的股价作为
，也可以采用内在价值作为P；2)：E是哪个E？ 正如下图，E至少都有四种：当前的
，预期的
，过去12个月平均的E(trailing twelve month, 即TTM)和预期未来12个月平均的E(next twelve month, 即NTM)。
图1：PE的搭配
或许有人说不就只有这几种吗？不算多。事实上，笔者只是列举了一下较常用的(不过笔者估计NTM一些人可能听都没听过)。其次，恐怖的不是它们这几种，而是它们和价格在一起形成的搭配，例如：例如
是大名鼎鼎的静态市盈率，
是大名鼎鼎的动态市盈率，
则是TTM市盈率。但还有不为人所熟知的，例如
，基本面调整的静态市盈率，基本面调整的动态市盈率，基本面调整的ttm市盈率等等，有8个之多。更别提它们林林总总衍生出的其它公式还有变形， 尤其是分子以内在价值进行基本面调整的PE还和绝对估值法扯上了关系。若是再加上取PE倒数获得股价收益率，除以增长率得到PE/g，上面这些公式又可以进一步拓展。。。
笔者毫不夸张的说PE公式能写出朵花，因此笔者本期取的名字“相对估值模型中的变形金刚”倒也称得上是实至名归。对于这些公式和这个指标的优缺点，笔者不想多谈， 也觉得没有意义，因此这些东西就直接省略吧。感兴趣的读者可以自行搜索，随便问问度娘都是万字长文，问问雪球，上面的大拿给你讲得透得不能再透。
市盈率（股票财务术语）_百度百科 (baidu.com)
https://baike.baidu.com/item/%E5%B8%82%E7%9B%88%E7%8E%87/90136?fr=aladdin
在写这篇博客前笔者浏览了许多关于PE指标的文章，目的当然不是为了东抄一点西抄一点，最后作出一篇大杂烩。既然本期笔者打算写这个被写烂了的指标，自然是要写点别人没有写过的东西。
2. 相对vs绝对
请大家做一个选择题：哪种估值法更好？A：绝对估值 B：相对估值
或许还应该有个选项，各有各的优点，各有各的缺点。但笔者认为在股票交易中相对估值更占优势。不知道有多少人想过绝对估值所绝对的是什么，相对估值所相对的是什么。笔者以为绝对估值所估计的是内在价值，而所谓相对肯定是有个参照物，它既可相对于同行业进行估计，又可以相对于历史进行估计。这赋予了相对估值更灵活，更能体现市场的特性。换句话说，市场是在不断波动的，绝对估值很难体现市场的波动，因为它是个绝对的估计值。相对估值却可以让我们寻找到那个相对估值更低的标的。尤其在市场动量效应下，这种体现市场特性的估值方式往往能获得比绝对估值更好的表现。
目前相对估值法要么基于行业平均，要么基于历史数据，是否有其它的思路。下面笔者将从从财报的角度对PE这个指标进行个小改造。
3. PE指标里的不合理因素
PE属于相对估值法的一种，其分子每股收益来自于损益表中的净利润。对于很多公司而言，净利润受公司经营，外部环境影响，波动往往是比较大的，甚至财报的一些不合理估计或计量，例如折旧的计量，存货的减值估计，对现金流归属，流动资产/非流动资产资产等划分方式都会对净利润造成影响。由于会计估计问题每家公司要具体去分析，很难给出一个具有普适性的方法，因此笔者着重从公司经营，外部环境影响对净利润造成的影响来对PE指标进行改造。通过将一些不合理的因素从PE指标中剔除，从而得到一个更为合理的PE指标，将之与市场上能观测到的PE指标进行比较便可得到一个新的相对高估/低估结论。
3.1 EPS拆解
既然已经明确净利润受公司经营，外部环境影响，波动往往是比较大的，那么现在的目标便是反向操作，平滑净利润中的不合理波动(插入公式用中文会乱码，下面笔者以英文代替)。
接下来用杜邦分析的原理对净利润动个小脑筋(BV是指账面价值book value， NI是净利润)：
![NI = \frac{NI}{BV of Equity} \times BV of Equity \left [ 1 \right ]](http://img.e-com-net.com/image/info8/6665c4ee6f80477e8e4f18694dd92eed.gif){kind=small}
神奇的事情就发生了：
![\frac{NI}{BV of Equity} = ROE \left [ 2 \right ]](http://img.e-com-net.com/image/info8/272ef0bc0bab4a6c9d94b7da886c51c2.gif){kind=small}
联立1，2式， 于是：
![NI = ROE \times BV of Equity\left [ 3 \right ]](http://img.e-com-net.com/image/info8/946136dd1ac14855816583f28a32b175.gif){kind=small}
这个式子与PE的分子EPS唯一有联系的是净利润，两边同时除以发行的股数(BVPS为每股账面价值或者说每股净资产book value per share)：
![EPS = ROE \times BVPS\left [ 4 \right ]](http://img.e-com-net.com/image/info8/b092637aee5543af8dbc4a4eb24a43cf.gif){kind=small}
4式中的EPS已经被完美拆分成两个指标，ROE及每股账面价值。原理与杜邦拆解类似，将一个指标拆分为多个有意义的部分进行分析。既然拆出了ROE这个式子甚至还可以对ROE使用真正的杜邦拆解继续拆下去， 不过拆到这里已经足够笔者分析用，就不继续往下演算了。
3.2 EPS分析
既然已经拆出两部分，那么我们就来分析一下这两部分的性质。 首先是ROE，其实导致PE大幅波动的大部分原因就是来自于ROE。ROE是直接与利润表科目变动挂钩的，净利润的异常波动会直接作用在ROE上，因此ROE也是笔者要进行平滑的对象。
其次是每股账面价值，这个指标我们乘以发行在外股数后其实就是资产负债表里的权益类科目。 笔者认为该指标能平滑更好，若不能平滑也无伤大雅。 因为经营波动更多体现在净利润上，而利润表的科目变化是通过勾稽关系与资产负债表相联系，可以说每股账面价值虽然受净利润影响，但净利润始终只是权益端一个科目而已， 影响已经被大大降低。另外笔者认为我们也很难将心思打到这个指标上平滑，因为每股账面价值， 或者说它的另一个名字——每股净资产，光看名字就知道了，企业的净资产，这个指标很大程度上体现了企业规模的增长。 换句话说由于企业估值所带来的市盈率估值笔者把它看作是合理的，是不该被平滑的，因此也就不动它了。
不过净利润毕竟也作用到每股账面价值上，若说一点影响也没有那也不尽然，只是若果把BVPS作为一个整体平滑，平滑掉的不仅仅有不合理因素，还把合理因素也给平滑掉了，并且这个不合理因素仅仅只是造成较小影响，思来想去实在是不划算。 不过感兴趣的读者也可以继续拆解每股账面价值，只平滑掉其中的净利润影响，不过笔者还是认为意义不大。
3.3 EPS平滑方式
说到平滑，不能干讲不带数据，下面代码走起。 数据方面笔者选择了Tushare金融数据库，通过简单的导入模型并调用接口即可快速稳定获取数据，比累死累活写爬虫方便不少。
下面导入相关模块：
import tushare as ts
import pandas as pd
import matplotlib.pyplot as plt笔者先获取EPS的季度数据，在进行数据处理前先将数据输出看看有什么特征, 由于Tushare输出的数据是倒序还有一些重复值，这里请求数据后稍加处理并输出到折线图上：
token = token #输入自己的tushare token
code = code ##输入公司代码
pro = ts.pro_api(token)
data = pro.income(ts_code=code, start_date='20160101', end_date='20220416',
fields='ts_code,end_date,basic_eps,diluted_eps')[::-1]
data.dropna(inplace = True)
data.index = range(len(df))
date = []
lst_delta = []
lst_eps = []
for i in df["end_date"][1:]:
if "0331" in str(i):
row = df[(df["end_date"]== i)].index.tolist()[0]
lst_delta.append(df["basic_eps"][row])
date.append(i)
lst_eps.append(df["basic_eps"][row])
else:
row = df[(df["end_date"] == i)].index.to_list()[0]
delta = float(df["basic_eps"][row] - df["basic_eps"][row + 1])
lst_delta.append(delta)
date.append(i)
lst_eps.append(df["basic_eps"][row])
data = {"date":date, "eps":lst_eps, "delta_eps":lst_delta}
eps = pd.DataFrame(data)
plt.figure(figsize = (15,6))
plt.plot(eps["date"], eps["delta_eps"], linewidth = 1, color = "black", linestyle = "-", marker = ".")
plt.plot(eps["date"], eps["eps"], linewidth = 1, color = "red", linestyle = "--", marker = ".")
plt.xticks(fontsize = 10, rotation = 90)
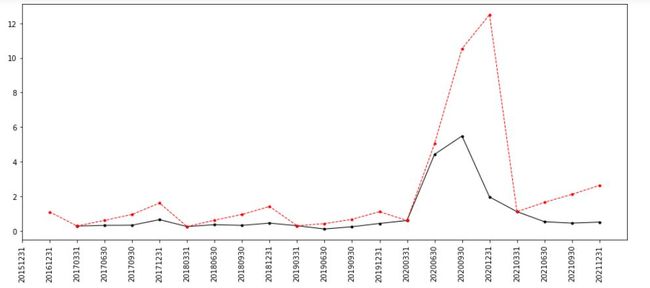
plt.show() 笔者计算了一下EPS的变化量(黑)并一起随EPS(红)输出得：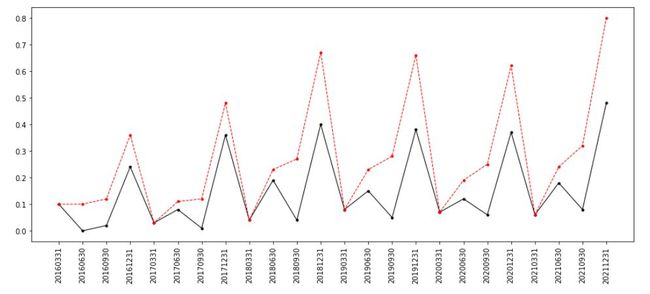
图2：某公司EPS季度数据
可以说这个公司经营还是十分稳定的，并且EPS呈现很强的时间序列特征，教统计学的老师估计能乐呵了，这么标标准准的的数据简直是教学必备， 但事实上这是笔者一家业绩非常稳定的公司，有好些公司的数据是乱七八糟的毫无规律可言，例如图3某口罩概念公司。
图3：某口罩概念公司EPS季度数据
可以看到的是疫情一来对公司基本面带来多大影响，但把疫情那会的时间拉长到现在来看，那时候的EPS从0.几上升到整整12，几十倍如此巨额的上涨依旧只是昙花一现，风采不再。
现状其实笔者已经po了两种类型的公司，1)：暴发户；2)：低调的土豪，在笔者看来对这两种公司的平滑方式是不同的，暴发户型的公司就应该狠狠往下调，均值回归的想法。 而低调土豪型的公司应该以时间序列的眼光去看，如果用均值回归反而容易低估，比较历史均值是在低位， 这类公司稳健的上升，说不好上去就不会下来了，很难说以后会产生均值回归。
出于计算简便，笔者这里就统一采用均值回归的方式对历史的ROE取均值进行平滑。
3.4 EPS平滑
获取ROE，每股账面价值(bps)数据并和刚才一样输出到折线图：
df = pro.query('fina_indicator', ts_code='603019.SH', start_date='20160101', end_date='20220416', fields="end_date,roe, bps, eps")
df.dropna(inplace = True)
df = df[::-1]
df.index = range(len(df))
plt.plot(df["end_date"], df["roe"], linewidth = 1, color = "b",linestyle = "-", marker = ".")
plt.plot(data["end_date"],data["bps"], linewidth = 1 , color = "red", linestyle = "--", marker = ".")
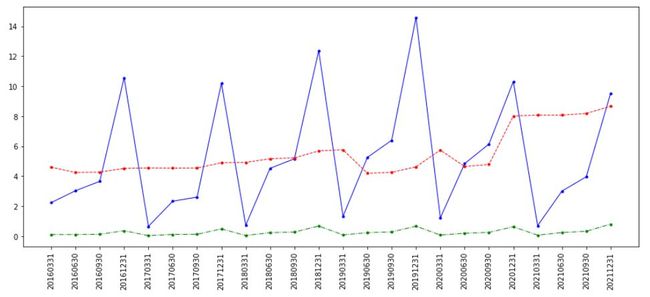
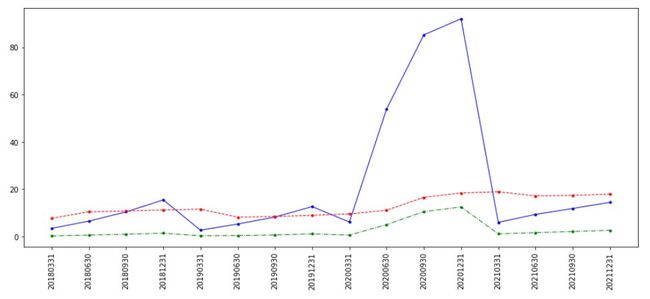
plt.plot(data["end_date"],data["eps"], linewidth = 1 , color = "green", linestyle = "-.", marker = ".")
图4：低调的土豪ROE(蓝)，每股账面价值(红)和EPS(绿)
图5：暴发户ROE(蓝)，每股账面价值(红)和EPS(绿)
下面用ROE均值同时对这两个类型公司平滑并得到平滑后的EPS：
mean_roe = df["roe"].mean()
nor_eps = df["bps"] * mean_roe/100 # ROE是带百分比数，除回去
plt.figure(figsize = (15,6))
plt.plot(df["end_date"], nor_eps, linewidth = 1, color = "orange", linestyle = "-", marker = ".")
plt.plot(df["end_date"], df["eps"], linewidth = 1, color = "blue", linestyle = "--", marker = ".")
plt.xticks(fontsize = 10, rotation = 90)
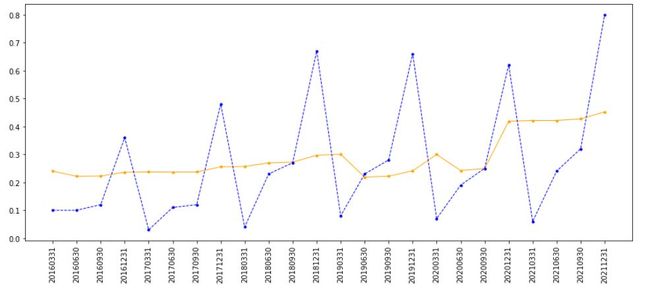
plt.show()
图6：低调的土豪EPS(蓝)和平滑后的EPS(黄)
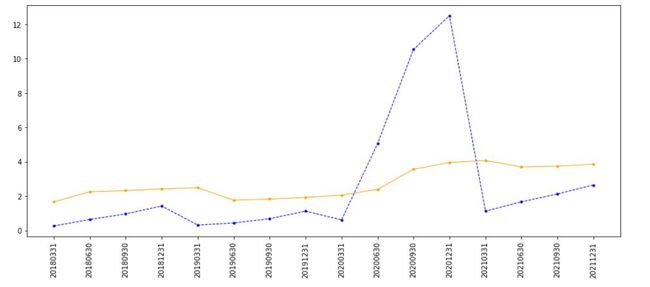
图7：暴发户EPS(蓝)和平滑后的EPS(黄)
可以看到，两类公司的平滑后EPS都具有波动小，异常波动弱化的特点，尤其针对暴发户型公司尤其明显，这种平滑所产生天然的优良性质让笔者把它做出来的一瞬间就爱上了它。
4. 根据平滑后的EPS计算新的PE指标
接下来只需要很简单的根据平滑出来的EPS带入PE进行计算即可， 说是简单，代码里碰到不少数据问题，因此写得稍微复杂了一些：
mean_p = []
pe = []
for i in df["end_date"]:
if i == "20160331":
weekly = pro.weekly(ts_code=code, start_date='20160101', end_date=i, fields='close')
p = float(weekly.mean())
mean_p.append(p)
try:
pe_lst = pro.query('daily_basic', ts_code=code, trade_date= i,fields='pe')
except:
pe_lst = pro.query('daily_basic', ts_code=code, trade_date= str(int(i) - 3),fields='pe')
pe.append(float(pe_lst["pe"][0]))
print(p, i, pe[-1])
else:
index = float(df[(df["end_date"] == i)].index.to_list()[0]) - 1
weekly = pro.weekly(ts_code=code, start_date=df["end_date"][index], end_date= i, fields='close')
p = float(weekly.mean())
mean_p.append(p)
try:
pe_lst = pro.query('daily_basic', ts_code=code, trade_date= i,fields='pe')
except:
pe_lst = pro.query('daily_basic', ts_code=code, trade_date= str(int(i) - 3),fields='pe')
pe.append(float(pe_lst["pe"][0]))
new_data = {"mean_p": mean_p, "nor_eps": list(nor_eps), "PE_ratio": pe}
data = pd.DataFrame(new_data)
nor_pe = data["mean_p"]/ data["nor_eps"]得到PE, 平滑后的PE及股价，将数据输出到折线图：
ax1 = plt.figure(figsize=(15, 6)).add_subplot(111)
line_pe = ax1.plot(df["end_date"][1:], data["PE_ratio"], linewidth=1, color="red", linestyle="-", marker=".",
label="PE")
line_npe = ax1.plot(df["end_date"][1:], nor_pe, linewidth=1, color="orange", linestyle="-", marker=".",
label="Normalized_PE")
plt.xticks(fontsize=10, rotation=320)
plt.xlabel("date")
plt.ylabel("PE")
plt.title(code + " Normalized PE")
ax2 = ax1.twinx()
line_p = ax2.plot(df["end_date"][1:], data["mean_p"], linewidth=1, color="blue", linestyle="--", marker=".",
label="Price")
plt.ylabel("Price")
lines = line_pe + line_npe + line_p
plt.legend(lines, [l.get_label() for l in lines])
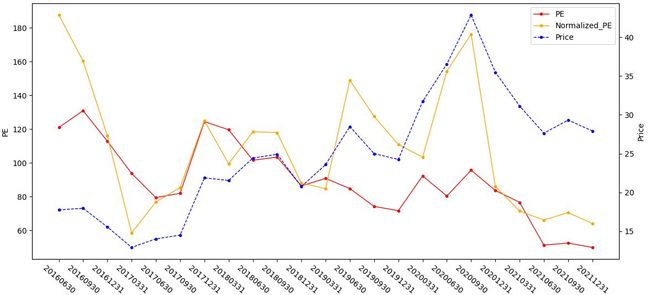
plt.show()
图8：低调的土豪
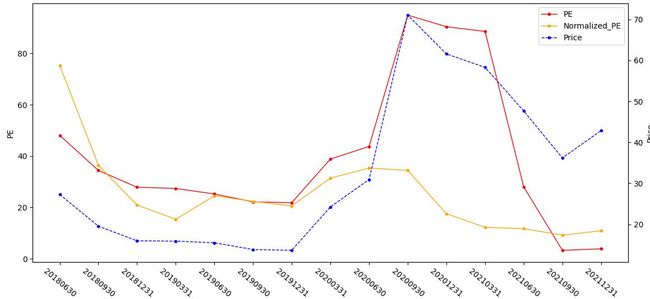
图9：暴发户
把最后的结果都输出，可以看到，暴发户公司虽然20年PE，EPS都急剧增加，实际经过笔者调整的PE却依旧趴在地上，虽然说PE是越低越好，但图9这种现象却并不是一件好事情，所谓相对估值相对估值，我们所相对的目标便是笔者经过平滑调整而出的PE黄线，当红线向上远离黄线很多时说明公司目前市场上说能观测到的PE(红线)已经远远超过了它应该在的位置(黄线)， 也就是相对高估！
从图8看，这个公司总的基本面十分稳健，业绩也没有太大异常波动，黄线一直位于红线上方，意味着公司目前市场上能观测到的PE是低估的，到20年3月黄线位于红线上方很远时股价还迎来一波非常可观的上涨。虽然目前黄线一直有下行向红线靠的趋势， 但总的风险比起口罩概念好上很多。
5. 整合代码
下面对之前写的代码整合成了函数形式：
def data_mod(code, start, end):
df = pro.query('fina_indicator', ts_code=code, start_date=start, end_date=end, fields="end_date,roe, bps, eps")
df.drop_duplicates(keep='first', inplace=True)
df.dropna(inplace=True)
df = df[::-1]
df.index = range(len(df)) # 重置索引
weekly = ts.pro_bar(ts_code=code, freq='W', adj='qfq', start_date=start, end_date=end)
weekly.drop_duplicates(keep='first', inplace=True)
weekly.dropna(inplace=True)
weekly = weekly[::-1]
weekly.index = range(len(weekly))
pe_lst = pro.query('daily_basic', ts_code=code, start_date=start, end_date=end, fields='trade_date, pe')
pe_lst.drop_duplicates(keep='first', inplace=True)
pe_lst.dropna(inplace=True)
pe_lst = pe_lst[::-1]
pe_lst.index = range(len(pe_lst))
return df, weekly, pe_lst
def pe_mod(pe_lst, begining, ending):
pe_data = []
for pe_date in pe_lst["trade_date"]:
if float(begining) <= float(pe_date) <= float(ending):
row = int(pe_lst[(pe_lst["trade_date"] == pe_date)].index.to_list()[0])
pe_data.append(pe_lst["pe"][row])
else:
pass
if len(pe_data) != 0:
mean_pe = sum(pe_data) / len(pe_data)
return mean_pe
else:
return None
def price_mod(data, begining, ending):
price = []
for trade_date in data["trade_date"]:
if float(begining) <= float(trade_date) <= float(ending):
row = int(data[(data["trade_date"] == trade_date)].index.to_list()[0])
price.append(data["close"][row])
if len(price) != 0:
return float(sum(price) / len(price))
else:
return None
def normalization(code, start, end):
df, weekly, pe_lst = data_mod(code, start, end)
mean_p, pe, nor_eps = [], [], []
for i in df["end_date"][1:]:
index = int(df[(df["end_date"] == i)].index.to_list()[0])
normalized = float(df["roe"][:index].mean() * df["bps"][index] / 100)
nor_eps.append(normalized)
if i == df["end_date"][1]:
beg = df["end_date"][0]
else:
beg = df["end_date"][index - 1]
p = price_mod(weekly, beg, i)
mean_p.append(p)
pe_mean = pe_mod(pe_lst, beg, i)
pe.append(pe_mean)
print("\r正在获取{}的pe, 季度均价".format(i), end="")
data = pd.DataFrame({"mean_p": mean_p, "nor_eps": nor_eps, "PE_ratio": pe})
nor_pe = data["mean_p"] / data["nor_eps"]
print("\nPE正则化完成，打印图表")
ax1 = plt.figure(figsize=(15, 6)).add_subplot(111)
line_pe = ax1.plot(df["end_date"][1:], data["PE_ratio"], linewidth=1, color="red", linestyle="-", marker=".",
label="PE")
line_npe = ax1.plot(df["end_date"][1:], nor_pe, linewidth=1, color="orange", linestyle="-", marker=".",
label="Normalized_PE")
plt.xticks(fontsize=10, rotation=320)
plt.xlabel("date")
plt.ylabel("PE")
plt.title(code + " Normalized PE")
ax2 = ax1.twinx()
line_p = ax2.plot(df["end_date"][1:], data["mean_p"], linewidth=1, color="blue", linestyle="--", marker=".",
label="Price")
plt.ylabel("Price")
lines = line_pe + line_npe + line_p
plt.legend(lines, [l.get_label() for l in lines])
plt.show()
def main():
code = input("键入代码")
start = input("开始日期")
end = input("结束日期")
normalization(code, start, end)
if __name__=='__main__':
main()6. 写在后面
本文通过财务手段对PE指标进行平滑，尽管笔者对这个指标偏爱有加，不过也要看到其缺点，例如：亏损企业没有PE怎么办？由于使用了财报，这个指标很大程度上还是滞后的，同时笔者也不建议在发行没多久的新股上使用。关于这个指标的改进前文有所提到，这里笔者再对其补充： 本文笔者仅仅只是对PE的分母进行分析，事实上还有个分子，完全可以结合相对估值模型算出一个基本面调整并且平滑后的PE指标，相关的绝对估值模型例如DDM笔者早在前面几期就阐述过，这里也不再赘述。
(93条消息) 浅谈估值模型（一）实现GGM的理想国（附代码）_Simon Cao的博客-CSDN博客_估值模型https://blog.csdn.net/simon1223z/article/details/119935415?spm=1001.2014.3001.5502 只是笔者认为绝对估值，至少DDM的条件太过苛刻，就算改造成功或许意义也不是很大因此没有继续进行，感兴趣的读者可以继续研究研究，若有什么成果可以分享一二。
笔者在本期的标题末尾加了个I，正如前文所提到的，PE指标远远不是表面上那么简单，如果有机会笔者再进行分享其它好玩又有用的PE估值方式。您若不弃，我们风雨共济。