opencv-python实现虹膜瞳孔内外圆检测

一、霍夫变换

本文主要介绍霍夫变换检测直线和圆的原理。

霍夫变换是图像处理中从图像中识别几何形状的基本方法之一，应用很广泛，也有很多改进算法。主要用来从图像中分离出具有某种相同特征的集合图像（如，直线，圆等）。最基本的霍夫变换是从黑白图像中检测直线（线段）。

1、直线检测

1.1 直线的表示方式

对于平面中的一条直线，在笛卡尔坐标系中，常见的有两点式，点斜式表示方式。然而在Hough变换中，考虑的是另外一种表示方式：使用($r,\theta$)$来表示一条直线。其中，r为该直线到原点的距离，$\theta$为该直线的垂线与x轴的夹角。如图下所示：

$

也就是霍夫变换中表示一条直线的参数变成了（r,$\theta$）。

2.如何判断多个点是否在同一直线上

当我们的对象变成点时，我们知道一个点可以发射出无数条直线，根据霍夫变换的直线表达形式，假设这个点为i,则通过这个点的直线我们用（$r_i,{\theta }_i$）表示。再假设一个点为j，则通过点j的一系列直线我们用（$r_j,{\theta }_j$）表示。我们知道两点决定一条直线，所以这两个点的直线必定有$r_i=r_j,{\theta }_i={\theta }_j$的时候。
那如果是三个点呢，假设第三个点是k，则通过k点的一系列直线为（$r_k,{\theta }_k$）,如果三点在一条直线上，那必定有某个$r_i=r_j=r_k=r,{\theta }_i={\theta }_j={\theta }_k=\theta$。
在霍夫变换检测直线时我们需要找到这样一样直线，如何找到这条直线呢？

3.如何检测出直线

使用hough变换来检测直线的思想就是：为每一个点假设n个方向的直线，通常n=180，此时检测的直线的角度精度为1°，分别计算这n条直线的$（r,\theta ）$坐标，得到n个坐标点。如果要判断的点共有N个，最终得到的$（r,\theta ）$坐标有N * n个。有关这N * n个（r,theta）坐标，其中$\theta$是离散的角度，共有180个取值。
最重要的地方来了，如果多个点在一条直线上，那么必有这多个点在theta=某个值theta_i时，这多个点的r近似相等于$r_i$。也就是说这多个点都在直线$（r_i,{\theta }_i）$上。
下面拿个例子说明：
如果空间中有3个点，如何判断这三个点在不在一个直线上，如果在，这条直线的位置为：

这个例子中，对于每个点均求过该点的6条直线的（r,$\theta$）坐标，共求了3 * 6个（r,$\theta$）坐标。可以发现在$\theta$=60时，三个点的r都近似为80.7，由此可判定这三个点都在直线（80.7，60）上。
通过 $r0\theta$ 坐标系可以更直观表示这种关系，如下图：图中三个点的$（r,\theta ）$曲线汇集在一起，该交点就是同时经过这三个点的直线。
通过 r * $\theta$ 坐标系可以更直观表示这种关系，如下图：图中三个点的（r,$\theta$）曲线汇集在一起，该交点就是同时经过这三个点的直线：

2.Hough圆检测

继使用hough变换检测出直线之后，顺着坐标变换的思路，提出了一种检测圆的方法。

2.1如何表示一个圆？

与使用（r,$\theta$）来表示一条直线相似，使用（a,b,r）来确定一个圆心为（a,b）半径为r的圆。
某个圆过点$（x_1,y_1）$，则有：$(x_1-a_1)^2 + (y_1-b_1)^2 = r_1^2 $。那么过点$（x_1,y_1）$的所有圆可以表示为$（a_1(i),b_1(i),r_1(i)）$，其中$r_1$\in （0，无穷），每一个i值都对应一个不同的圆，$（a_1(i),b_1(i),r_1(i)）$表示了无穷多个过点$（x_1,y_1）$的圆。

2.2 如何确定多个点在同一个圆上？

如上说明，过点（x1,y1）的所有圆可以表示为$（a_1(i),b_1(i),r_1(i)）$，过点$（x_2,y_2）$的所有圆可以表示为$（a_2(i),b_2(i),r_2(i)）$，过点$（x_3,y_3）$的所有圆可以表示为$（a_3(i),b_3(i),r_3(i)）$，如果这三个点在同一个圆上，那么存在一个值$（a_0,b_0,r_0）$，使得$ a_0 = a_1(k)=a_2(k)=a_3(k) 且b_0 = b_1(k) = b_2(k) = b_3(k) 且r_0=r_1(k)=r_2(k)=r_3(k)$，即这三个点同时在圆$（a_0,b_0,r_0)上。$
从下图可以形象的看出：

首先，分析过点$（x_1,y_1）$的所有圆$（a_1(i),b_1(i),r_1(i)）$，当确定$r_1(4i)$时 ，$（a_1(i),b_1(i)）$的轨迹是一个以$（x_1,y_1,r_1(i)）$为中心半径为$r_1(i)$的圆。那么，所有圆$（a_1(i),b_1(i),r_1(i)）$的组成了一个以（x1,y1,0）为顶点，锥角为90度的圆锥面。
三个圆锥面的交点A 既是同时过这三个点的圆。

opencv-python实现虹膜瞳孔边缘检测

cv2.HoughCircles函数说明：
用函数 cv2.HoughCircles(image, method, dp, minDist, circles, param1, param2, minRadius, maxRadius) ， 其参数解释如下：
（1）image: 输入图像，需要灰度图
（2）method: 检测方法，常用CV_HOUGH_GRADIENT
（3）dp: 为检测内侧圆心的累加器图像的分辨率于输入图像之比的倒数，如dp=1，累加器和输入图像具有相同的分辨率，如果dp=2，累计器便有输入图像一半那么大的宽度和高度
（4）minDist: 表示两个圆之间圆心的最小距离
（5）circles: 找到的圆的输出向量,一般不设置
（6）param1: 默认值100，它是method设置的检测方法的对应的参数，对当前唯一的方法霍夫梯度法cv2.HOUGH_GRADIENT，它表示传递给canny边缘检测算子的高阈值，而低阈值为高阈值的一半
（7）param2:默认值100，它是method设置的检测方法的对应的参数，对当前唯一的方法霍夫梯度法cv2.HOUGH_GRADIENT，它表示在检测阶段圆心的累加器阈值，它越小，就越可以检测到更多根本不存在的圆，而它越大的话，能通过检测的圆就更加接近完美的圆
（8）minRadius：默认值0，圆半径的最小值
（9）maxRadius：默认值0，圆半径的最大值

代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread("E:\matlab_file\hongmoshibie\pic2.png")
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #灰度图像

plt.subplot(121),plt.imshow(gray,'gray')
plt.xticks([]),plt.yticks([])
#使用HoughCircles对灰度图像进行霍夫变换
circles1 = cv2.HoughCircles(gray,cv2.HOUGH_GRADIENT,1,
100,param1=100,param2=30,minRadius=50,maxRadius=100)
circles = circles1[0,:,:] #提取为二维
circles = np.uint16(np.around(circles)) #四舍五入，取整
for i in circles[:]:
    cv2.circle(img,(i[0],i[1]),i[2],(255,0,0),5) #画圆
    cv2.circle(img,(i[0],i[1]),2,(255,0,255),10) #画圆心

plt.subplot(122),plt.imshow(img)
plt.xticks([]),plt.yticks([]);

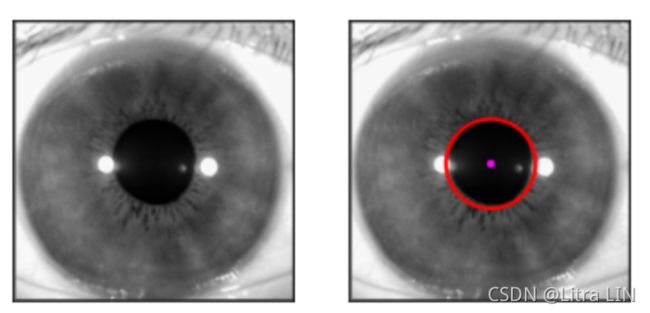
瞳孔外圆检测：
调整minRadius、maxRadius参数（将其分别设置为：minRadius=200,maxRadius=290，代码基本不变），即可检测出瞳孔的外圆。

Tips:
1.在霍夫圆检测之前进行高斯滤波，减少噪声
2.以前利用霍夫圆检测经常出现检测不到圆，或错误检测的情况，实则是因为参数没有设置到位。应该小心调节的参数有:
minDist:根据实际情况调节，越小检测的圆越多，错误率越大
param2：这个参数以前没有注意过，针对于虹膜检测，目标圆是较小的，所以这个值理应设置的小一点。
minRadius,maxRadius:圆半径范围