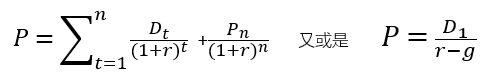浅谈估值模型（一）实现GGM的理想国（附代码）

目录

一、写在前面

二、缘起

三、描绘一个现实中的理想世界

1：预期收益率r

2：下一期股利与增长率g

3：永续增长率g

 4：内在价值计算

四、模型结果        

五、写在后面

---

一、写在前面

1：本文主要讨论戈登增长模型的优化及现实意义；另外，本文使用python实现模型并以某证券为例进行估值

2：本文主要行情数据通过Tushare(ID：444829)金融大数据平台接口获取， 部分财务指标，利率指标通过爬虫获取

3：笔者希望搭建出一套交易体系，原则是只做干货的分享。后续将更新更多模块，但工作学习之余的闲暇时间有限，更新速度慢还请谅解

4：文中假设与观点是基于笔者对模型及数据的一孔之见，若有不同见解欢迎随时留言交流

5：模型实现基于python3.8

二、缘起

        先来段开场白，笔者认为一些理念性的东西价值远超过代码和模型本身，不过对长篇大论不感兴趣的小伙伴们可以直接跳过，从第三部分开始看~

        戈登增长模型（Gordon Growth Model, GGM) 笔者常戏称之为哥哥们。 戈登增长模型其实是股息贴现模型（DDM）的一种优化，通过计算公司预期未来支付给股东的股利现值，来确定股票的内在价值，即是股利永续流入。GGM在上世纪五十年代被John Burr Williams发布出来，而它的弟弟——DDM则早在上世纪三十年度被提出。事实上，那个时代对股票的理念便是买入并持有以赚取分红。现如今近百年过去，这样的理念早被急不可耐的"行为金融学大师们"抛弃；尤其在A股，市场上的投资者多为买入并持有以赚取差价。

        巴菲特说过：“如果没有持有一支股票十年的打算就不要买入”。老人家的底气其实可以用这样的公式解释：站在今天看未来可以获得的好处，如果超过今天所付出的对价那便赚了。

        在笔者眼中这是比薛定谔的猫还要高维度的存在——这个盒子里明天有没有猫。作为一个唯物主义无神论者，我甚至没有能力知道现在盒子里是否有猫，更遑论未来股价是多少？ 事实是小到小散们的怒掷一手的交易，大到分析师报告里的纸上谈兵（  买！），只要不是有能力画K线的的主力，或是内幕的知(lao)情(shu)人(cang)，我们都在拼命的引入未来函数。

        什么？巴菲特？他老人家也引入了，不然20年疫情抄底航空股一抄抄在半山腰？

 

        （本文只论基本面，老缠师请不要与我论道）佛陀有言：“一切有为法，皆待缘而起”。世间的结果都是因各种因缘而成，即为缘起。股价和股利亦是如此，笔者认为大可不必视未来函数如洪水猛兽，但其信号漂移是一定需要考虑的，我们所能做的就是加上限定条件，例如给我一只半透明的盒子或是一杆秤，那么可以通过观察盒子或是称重量间接知道盒子里是不是有猫。

         事实情况却远比薛定谔的猫来得复杂：首先它站在空间维度（今天会不会有猫）；对一个企业来说，目前所处行业，财务水平，管理层质量等等判断企业(盒子)会不会大概率产生持续的利润（猫)。其次是站在时间维度（明天会不会有猫）导致各种信号产生的漂移，这是痛点所在，股利是否能永续流入？企业能否以目前状况永续经营？外部黑天鹅事件，外部冲击et al. 万事皆可谓“缘起” 。

        第二种情况较为复杂，出于内容规划考虑，笔者想在后续模块中寻求更好的解法。

        第一种情况较为简单，但由于N-holding period 太过苛刻，对权益工具来说难以实现。本文就从相对现实一些的GGM切入。

三、描绘一个现实中的理想世界

        先为新世界导入必要的模块

import pandas as pd
import tushare as ts
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import seaborn as sns

        

        为了求出股价必须先求出：

1：预期收益率r

2：下一期股利与增长率g

3：永续增长率g

---

        为保证模型有效性，建议采用10年的数据，5年也可。接下来以某市场指数, 及某证券自2011年1月1日起，至2021年9月7日所有交易日数据为例进行演示（为避免荐股嫌疑就不展示具体代码了，下面相关信息也都会隐去）。以下结果均是通过row data计算得到，自己计算各种指标的最大的好处就是将一切问题可控，且可以进行很强的个性化处理。

1：预期收益率r

        r 的求法有很多，这里通过CAPM实现，即

 

        先来个可爱的迷你爬虫获取最新的国债利率做为无风险收益率rf，如果嫌麻烦也可以做好模型直接导入具体数值。table存的是国债收益率表，三年到十年都有，这里取三个月短期国债收益率做为无风险收益率，即table.loc[1,2]。

def risk_free(Date): ## Date: year-month-day
    url = "https://yield.chinabond.com.cn/cbweb-cbrc-web/cbrc/historyQuery?startDate=" + 
           Date+ "&endDate=" + Date+ "&gjqx=0&qxId=ycqx&locale=cn_ZH&mark=1 "
    content = pd.read_html(url)
    table = content[1]
    print('Risk_free rate（Short term (3 month) T-Bill）：', table.loc[1, 2], "%")
    return table.loc[1, 2]

        接着是市场回报及敏感系数beta 

        这里引入一款非常方便的数据获取模块tushare，通过简洁的数据接口可以获取各类金融数据，省去大把写爬虫的时间。通过这个链接Tushare大数据社区注册成功后即可通过自己的token便捷调用数据，具体可参考Tushare的技术文档。

        只需要对pro.daily传入证券代码及起止日期即可获取所有日线级别数据，并如法炮制获取市场指数数据。

def date_input(token, cp, mk,  start, end):
    pro = ts.pro_api(token)
    cp = pro.daily(ts_code=cp, start_date=start, end_date=end)         #company数据
    mk = pro.index_daily(ts_code=mk, start_date=start, end_date=end)   #market数据
    beta = beta_value(cp, mk) # 计算beat
    Mr = mean_value(mk)       # 计算市场回报率

        使用sklearn对日回报进行拟合，这里对没有数据的停牌交易日进行剔除以保证指数与个股数据是成对出现。

def beta_value(cp, mk):
    for i in mk['trade_date'].values:
        if i not in cp['trade_date'].values:
            # Match the market data-set with securities, some securities may halt
            mk = mk[~mk['trade_date'].isin([i])] # 剔除个股停牌日

    return_cp = cp ["pct_chg"] 
    return_mk = mk ["pct_chg"]
    return_cp = return_cp.reshape(-1, 1)
    return_cp = return_cp[::-1] 
    return_mk = return_mk.reshape(-1, 1)
    return_mk = return_mk[::-1]

    Mod = LinearRegression() 
    Mod.fit(return_mk, return_cp) # 采用线性回归对市场及个股数据进行拟合
    beta = Mod.coef_[0][0]        # 计算出相关系数，即β
    print("Beta is", beta)
    # print("R_square是", Model.score(return_mk, return_cp))
    return beta

        计算得该证券

        既然得到了十多年的数据，手痒顺便看下中心趋势及分布状况是什么样的

def dis_function(cp, mk):
    m, s = pd.Series(mk["pct_chg"]), pd.Series(cp["pct_chg"])
    print("market mean:",mk["pct_chg"].mean(),"market median:",mk["pct_chg"].median())
    print("security mean", cp["pct_chg"].mean(), "security median:",cp["pct_chg"].median())
    print("market skewness:",m.skew(),"market kurtosis:",m.kurt())
    print("security skewness:",s.skew(),"security kurtosis:",s.kurt())


    dataset = pd.DataFrame({"market": mk["pct_chg"].values, "security":             
              cp["pct_chg"].values})
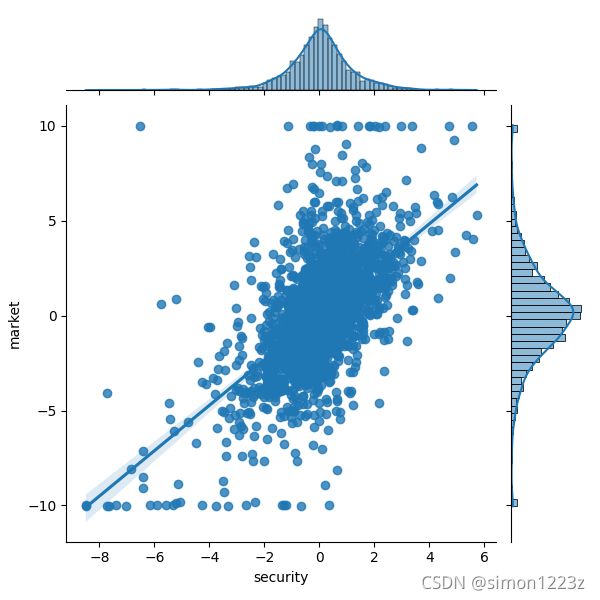
    sns.jointplot(x= "security", y = "market", data = dataset, kind = "reg")
    plt.show()

        可得： 

        近似是个正态，关于分布笔者会在后续的文章中用到，这里仅作展示。

        接着把指数的日涨跌幅均值计算出来并年化处理：

def mean_value(mk):
    mean = mk['pct_chg'].mean()
    mean_yield = ((1 + mean / 100) ** 365 - 1) * 100
    print("Average return of the Market（Suggest 10 years）：", mean_yield, "%")
    return mean_yield

计算得

        至此，我们便得到了所有计算回报率 r 的要件，调用之前的模块并计算r为：

rf = float(risk_free()) # Calculate risk free rate
beta_Mr = data_input(company, market, start, end)
beta = beta_Mr[0] # Beat value
Mr = beta_Mr[1]
expt_r = rf + beta * (Mr - rf)

计算可得E(r): 5.1745 %

2：下一期股利与增长率g

        第一个迷之信仰来了：现在没有分红，如何知道下一期股利？结合增长率g来看大概有几种解法：

        1）：公式法

        通过ROE*(1-Payout Ratio)求出增长率g，这个增长率即是假设公司的利润率不变，盈利效率不变，财务政策不变的情况下，可以实现的增长率。于是再使用当期股利乘以这个增长率以计算出下一期股利 。

        2）：历史数据法

        通过过去推未来，计算过去一段时间内的股利年化增长率，再用当期股利乘以这个增长率以计算出下期股利

        3）：夸下海口法

        由以上两种方式计算出g。根据分析师灵(pou)敏(gai)的职业判断对计算的g进行调整并向投资者夸下海口。

        如果结合内幕消息或是撞大运正好猜中，我们可以得到第四种解法：

        4）：什么都不干，直接把已知的下一期股利放入公式。

        可以看到以上三种方式都用到了增长率g的概念，后面会再对g进行讨论，接下来先以公式法为例进行计算。

        首先来个精致的爬虫从新浪上获取历史股利信息：

def craw_dividend(company): #start, end,
    url = "http://vip.stock.finance.sina.com.cn/corp/go.php/vISSUE_ShareBonus/stockid/" \
          + str(company.split(".")[0]) + ".phtml"
    table = pd.read_html(url, attrs={"id": "sharebonus_1"}, header=[2])
    div_inform = pd.DataFrame(table[0][::-1])

        print出表格一看，什。。什么！一年竟然分好几次红公司和不分红的铁公鸡？处理一下表格，不分红为0，分红多次的求其合计数做为该年股利。

# 接上一个代码块
year = []
div = []
div_hist = div_inform["派息(税前)(元)"]
for i in div_inform["公告日期"]:
    row = div_inform[(div_inform["公告日期"] == i)].index.tolist()
    div.append(float(div_hist[row].values))
    year.append(i.split("-")[0])
dataset = {"year": year, "dividend": div}
div_table = pd.DataFrame(data=dataset)  # 只包含分红信息和年份的表格

rows_list = []
for i in div_table["year"]:
    index = div_table[(div_table["year"] == i)].index.tolist()
    rows_list.append(div_table[(div_table["year"] == i)].index.tolist()) if index not in 
    rows_list else next
for rows in rows_list:
    if len(rows) == 1:
        continue
    else:
        total_div = 0
        for row in range(1, len(rows)):
            total_div = total_div + div_table["dividend"][rows[row]]
            div_table.drop(rows[row], inplace=True)
        div_table.loc[rows[0], "dividend"] = total_div + div_table["dividend"][rows[0]]
div_table.reset_index(drop=None, inplace=True)
print(div_table)
return div_table, div_inform  ## divd_inform has all div. information，div_table only has【year】and 【div】

        这里留了个口子把div_inform 也取了出来，方便以后写程序可以直接调用。

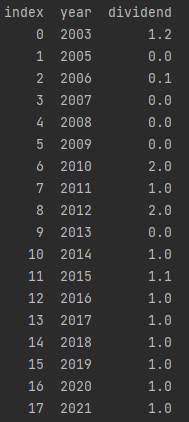
        得到div_table如下：

         感兴趣的小伙伴可以通过历史数据法计算推出下一期股利，这里采用公式法只取出当期股利。

3：永续增长率g

        通过ROE*(1-Payout Ratio)求出增长率g

        继续一个蠢萌的迷你爬虫获取ROE

def craw_roe(company):
    url 
="http://money.finance.sina.com.cn/corp/go.php/vFD_FinancialGuideLine/stockid/"+str(company.split(".")[0])+"/ctrl/2019/displaytype/4.phtml"
    ratio = pd.read_html(url, attrs={"id":"BalanceSheetNewTable0"})
    return ratio

        接着通过Tushare接口获取相关财务指标以计算g:

def tus_growth(ts_code,period):
    global growth
    period_beg = str(int(period) -1) +"1231"
    period = period+"1231"
    ratio_end = pro.query('fina_indicator', ts_code=ts_code , period=period)
    gl_table= pro.income(ts_code=ts_code, period=period, fields='ts_code,n_income', report_type=1)
    ratio_beg = pro.query('fina_indicator', ts_code=ts_code , period=period_beg)

    roe = float(ratio_end["roe"][0])                 # ROE
    re_beg =float(ratio_beg["retained_earnings"][0]) # Retain earning at the beg of period
    re_end= float(ratio_end["retained_earnings"][0]) # Retain earning at the end of period
    n_income = float(gl_table["n_income"][0])        # Net income

    growth = roe *(1-(re_end-re_beg)/ n_income)
    print("Growth rate of",ts_code,"is",growth,"%","with ROE:",roe, "  net income:",n_income," at the period "
                                                   "end of", str(period)[:4])
    return growth

 计算得：

        结合之前股利历史状况，1.3%的增速也可以理解。。可以视为几乎没有增速。净利润和后面的日期这些信息就不展示了。

        接下来，万事具备只欠东风！

 4：内在价值计算

         调用之前的模块，传入市场代码，证券代码，起止日期，股利计算日期，大功告成！

if __name__ == '__main__':
    market = input('Market Code')  # 000001.SH
    company = input('Security Code')  # 600522.SH
    start = input('Start Date(Dealing Day)')
    end = input('End Date(Dealing Day）')

#Clac risk free , beta & E(r)
    rf = float(risk_free()) # Calculate risk free rate
    beta_Mr = data_input(company, market, start, end)
    beta = beta_Mr[0] # Beat value
    Mr = beta_Mr[1]
    expt_r = rf + beta * (Mr - rf)
    print("Output", company, "E(r):", expt_r, "%")
# calc dividend at beginning
    div_table = craw_dividend(company)[0]
    div_date = input("Input a complete financial period (year) for dividend")
    div_date = str(div_date[:4])
    row = div_table[(div_table["year"] == div_date)].index.tolist()
    div_value = div_table.iloc[int(row[0])]["dividend"]
    print("The dividend for {0}".format(div_date),"is:", div_value)

# calc g
    div_date= int(div_date)-1 ## still need adjustment
    tus_growth(company, str(div_date))

# Formular(Golden growth model)
    price = div_value*(1+(growth/100)) / ((expt_r - (growth))/100)
    print("The intrinsic value of", company,"is", price)

      四、模型结果        

        该证券模型结果为：

        笔者对该结果颇为满意，笔者利用相对估值法计算也有着相似的价值。不管模型是不是真正估计到了这只明天盒子里薛定谔的猫，在笔者心里已经成功了。

五、写在后面

        程序可以个性化查看，但也可以批量跑，把Input的信息变成列表便利即可把大A四千家公司统统撸一遍。

        关于理想国：笔者所用公司是经过挑选的，换句话说只有符合条件的公司才能与我的世界契合。这基于以下几点条件或假设：

        1）：该公司增长率极低，因此股利折现时g的威力对模型没有什么影响；但对于一些高分红，高ROE的公司来说，该模型或面临失效；2）：模型结果是该公司在笔者眼中的价值，该公司经营基本面稳定，且未来长期永续经营，笔者也进行长期投资；3）：这家公司有足够多的数据（至少近十年）供计算，对于一些上市时间较短的公司，模型有效性或将大打折扣；

        我的世界也并非要一成不变的。现实情况是许多公司分红都是不稳定或呈现周期性波动，这样可以将过去几年的股利均值视为进行计算。增长率g也并非永续且固定，多阶段折现，采用更保守的方式折现都可以估计出一个区间，这个区间下限将是保守值，上线将是预警值。

        最后，笔者认为决定一个公司股价高度的是市值而并非其内在价值，内在价值只能决定一个均值回归时的中枢，以内在价值进行交易是不一定划算的。