Keras深度学习实战(3)——神经网络性能优化技术详解
Keras深度学习实战(3)——神经网络性能优化技术详解
-
- 0. 前言
- 1. 缩放输入数据集
-
- 1.1 数据集缩放的合理性解释
- 1.2 使用缩放后的数据集训练模型
- 2. 输入值分布对模型性能的影响
- 3. 批大小对模型准确率的影响
- 4. 构建深度神经网络提高模型准确性
- 5. 学习率对网络性能的影响
-
- 5.1 基础示例
- 5.2 MNIST 数据集上不同学习率对性能的影响
- 6. 不同损失优化器对模型性能的影响
- 小结
- 系列链接
0. 前言
我们已经学习了神经网络的基础概念,并了解了如何利用 Keras 库构建实用神经网络模型。同时我们还提到了,有多种超参数可以影响神经网络的准确性。在本节中,我们将详细介绍神经网络中各种超参数的作用,通过使用不同的超参数来优化神经网络性能。
1. 缩放输入数据集
缩放数据集是一个在网络训练之前提前对数据进行处理的过程,在此过程中,限制数据集中的数据范围,以确保它们不会分布在较大的区间。实现此目的的一种方法是将数据集中的每个数据除以数据集中的最大数据。 通常,缩放输入数据集能够提高神经网络的性能表现,是常用的数据预处理方法之一。
1.1 数据集缩放的合理性解释
在本节中,我们将了解缩放数据集能使神经网络性能更好的原因。为了了解缩放输入对输出的影响,我们对比在未缩放输入数据集时模型性能和在缩放输入数据集时的性能情况。
当输入数据未缩放时,在不同权重值的作用下 sigmoid 函数值如下表所示:
| 输入 | 权重 | 偏置 | sigmoid 值 |
|---|---|---|---|
| 255 | 0.01 | 0 | 0.93 |
| 255 | 0.1 | 0 | 1.00 |
| 255 | 0.2 | 0 | 1.00 |
| 255 | 0.4 | 0 | 1.00 |
| 255 | 0.8 | 0 | 1.00 |
| 255 | 1.6 | 0 | 1.00 |
| 255 | 3.2 | 0 | 1.00 |
| 255 | 6.4 | 0 | 1.00 |
在上表中,即使权重值在 0.01 到 6.4 之间变化,在经过函数 Sigmoid 后输出变化也不大,为了解释这一现象,我们首先回忆下 Sigmoid 函数的计算方法:
output = 1/(1+np.exp(-(w*x + b))
其中 w 是权重,x 是输入,b 是偏置值。
sigmoid 输出不变的原因是由于 w * x 的乘积很大(主要是因为 x 较大),导致 sigmoid 值始终落在 sigmoid 曲线的饱和部分中( sigmoid 曲线的右上角或左下角的值称为饱和部分)。而如果我们将不同的权重值乘以一个较小的输入数字,则结果如下所示:
| 输入 | 权重 | 偏置 | sigmoid 值 |
|---|---|---|---|
| 1 | 0.01 | 0 | 0.50 |
| 1 | 0.1 | 0 | 0.52 |
| 1 | 0.2 | 0 | 0.55 |
| 1 | 0.4 | 0 | 0.60 |
| 1 | 0.8 | 0 | 0.69 |
| 1 | 1.6 | 0 | 0.83 |
| 1 | 3.2 | 0 | 0.96 |
| 1 | 6.4 | 0 | 1.00 |
由于输入值较小,因此上表中的 Sigmoid 输出值会随权重的变化发生改变。
通过此示例,我们了解了缩放输入对数据集的影响,当权重(假设权重不具有较大范围)乘以较小输入值时,使输入数据能够对输出产生足够重要的影响。同样当权重值也很大时,输入值对输出的影响将变得不太重要。因此,我们一般将权重值初始化为更接近零的较小数值。同时,为了获得最佳的权重值,通常设置初始化权重的范围变化不大,比如权重在初始化期间采样介于 -1 和 +1 之间的随机值。
接下来,我们对使用的数据集MNIST进行缩放,并比较使用和不使用数据缩放对性能的影响。
1.2 使用缩放后的数据集训练模型
- 导入相关的包和
MNIST数据集:
from keras.datasets import mnist
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.utils import np_utils
import matplotlib.pyplot as plt
(x_train, y_train), (x_test, y_test) = mnist.load_data()
- 缩放数据集有多种方法。一种方法是将所有数据点转换为 0 到 1 之间的值(通过将每个数据点除以数据集中的最大值,在本例中最大值为 255),展平输入数据集并对其进行缩放,如下所示:
num_pixels = x_train.shape[1] * x_train.shape[2]
x_train = x_train.reshape(-1, num_pixels).astype('float32')
x_test = x_test.reshape(-1, num_pixels).astype('float32')
x_train = x_train / 255.
x_test = x_test / 255.
另一种流行的数据缩放方法是对数据集进行归一化,以使值转换到 -1 和 +1 之间,方法是用数据平均值减去数据点,然后将得到的结果除以原始数据集的标准差:
x ′ = ( μ − x ) σ x'=\frac {(\mu -x)} \sigma x′=σ(μ−x)
3. 将训练和测试输入的值缩放至 [0, 1] 后,我们将数据集的标签转换为独热编码格式:
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_test.shape[1]
- 构建模型并进行编译:
model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
上述模型与我们在《使用Keras构建神经网络》中构建的模型完全相同,唯一的区别是本节模型将在缩放后的数据集上进行训练。
- 拟合模型,如下所示:
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=64,
verbose=1)
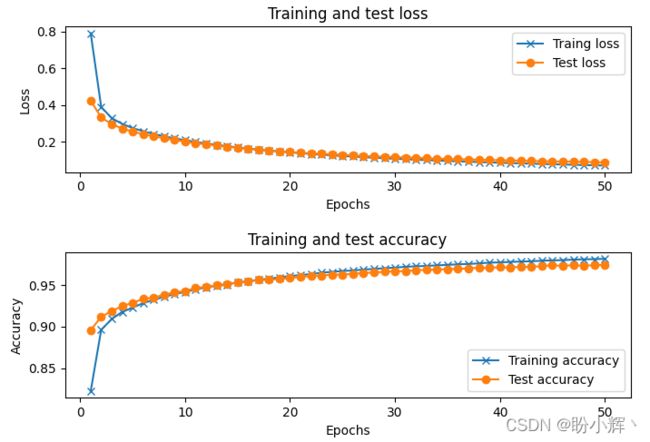
该模型的准确率约为 98.41%,而未缩放数据时训练的模型准确率在 97% 左右。绘制不同 epoch 的训练和测试的准确性以及损失值(绘制曲线图的代码与训练原始神经网络方法中使用的代码完全相同):
从上图中可以看出,与非缩放数据集训练的模型相比,训练和测试损失的变化较为平缓。尽管网络能够平稳的降低损失值,但我们看到训练和测试准确率之间存在较大差距,这表明在训练数据集上可能存在过拟合的情况。过拟合是由于模型针对训练数据过度拟合,这导致在测试数据集的性能不如训练数据集,泛化性能较差。
除了通过将值除以最大值来缩放数据集外,其他常用的缩放方法如下:
- 最小-最大归一化
- 均值归一化
- 标准方差归一化
2. 输入值分布对模型性能的影响
到目前为止,我们还没有查看 MNIST 数据集中值的分布情况,而输入值的不同分布可以改变训练速度。在本节中,我们将了解如何通过修改输入值以缩短训练时间,更快地训练权重。
在本节中,我们将构建与上一节完全相同的模型架构。但是,将对输入数据集进行一些小的更改:
- 反转背景色和前景色。本质上,是将背景涂成白色,数字涂成黑色。
我们首先从理论上分析像素值对模型性能的影响。由于黑色像素值为零,当此输入乘以任何权重值时,输出为零。这将导致黑色像素连接到隐藏层的权重值无论如何更改都不会影响损失值。但是,如果有一个白色像素,那么它将对某些隐藏节点值有所贡献,权重需要进行调整。
- 加载并缩放输入数据集:
from keras.datasets import mnist
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.utils import np_utils
import matplotlib.pyplot as plt
(x_train, y_train), (x_test, y_test) = mnist.load_data()
num_pixels = x_train.shape[1] * x_train.shape[2]
x_train = x_train.reshape(-1, num_pixels).astype('float32')
x_test = x_test.reshape(-1, num_pixels).astype('float32')
x_train = x_train / 255.
x_test = x_test / 255.
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_test.shape[1]
- 查看输入值的分布情况:
x_train.flatten()
前面的代码将所有输入展平到一个形状为 ( 28 × 28 × x _ t r a i n . s h a p e [ 0 ] = 47040000 28\times 28 \times x\_train.shape[0]=47040000 28×28×x_train.shape[0]=47040000) 的列表中。绘制所有输入值的分布情况:
plt.hist(x_train.flatten())
plt.title('Histogram of input values')
plt.xlabel('Input values')
plt.ylabel('Frequency of input values')
plt.show()
由于输入图像的背景为黑色,因此大多数输入都是零(黑色像素值)。
- 使用以下代码反转颜色,使得背景为白色,数字为黑色。
x_train = 1-x_train
x_test = 1-x_test
绘制图像:
plt.subplot(221)
plt.imshow(x_train[0].reshape(28,28), cmap='gray')
plt.subplot(222)
plt.imshow(x_train[1].reshape(28,28), cmap='gray')
plt.subplot(223)
plt.imshow(x_test[0].reshape(28,28), cmap='gray')
plt.subplot(224)
plt.imshow(x_test[1].reshape(28,28), cmap='gray')
plt.show()
反转颜色后生成图像的直方图如下所示:
可以看到,现在大多数输入值的值为 1。
- 使用与之前完全相同的模型架构:
model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=64,
verbose=1)
绘制不同 epoch 的训练和测试的准确率以及损失值:
可以看到,模型准确率下降到到 97%,相比之下,在未反转数据集的时(数据集中数据值多数为零),使用相同的 epoch 数、批大小和模型架构,训练得到的模型的准确率约为 98%。而像素值反转(数据集中数据值零较少)的情况下模型的精度为 97%,且训练过程比大多数输入像素为零的情况要慢得多。当大多数像素为零时,模型的训练更加容易,因为它只需要根据像素值大于零的少数像素值进行预测。但是,当大多数像素不为零时,需要微调更多的权重以减小损失值。
3. 批大小对模型准确率的影响
在之前的模型中,我们对于构建的所有模型使用的批大小 (batch size) 为均为 64。在本节中,我们将研究改变批大小对准确率的影响。 为了探究批大小对模型准确率,我们对比一下两种情况:
- 批大小为 4096
- 批大小为 64
与批大小较小的情况相比,批大小较大时,每个 epoch 中的权重更新次数较少。当批大小较小时,每个 epoch 会进行多次的权重更新,因为在每个 epoch 中,必须遍历数据集中的所有训练数据,因此如果每个 batch 使用较少的数据计算损失值,会导致每个 epoch 具有更多的 batch 才能遍历整个数据集。因此,batch 大小越小,相同 epoch 训练后的模型准确率越好。但是,还应确保批大小不能过小,以免导致过拟合。
在先前的模型中,我们使用了批大小为 64 的模型。本节中,我们继续使用相同的模型架构,仅修改模型训练的批大小,以比较不同批大小对模型性能的影响。预处理数据集并拟合模型:
(x_train, y_train), (x_test, y_test) = mnist.load_data()
num_pixels = x_train.shape[1] * x_train.shape[2]
x_train = x_train.reshape(-1, num_pixels).astype('float32')
x_test = x_test.reshape(-1, num_pixels).astype('float32')
x_train = x_train / 255.
x_test = x_test / 255.
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_test.shape[1]
model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=4096,
verbose=1)
代码的唯一更改是模型拟合过程中的 batch_size 参数。绘制训练和测试的准确率和损失值:
在上图中可以注意到,与批大小较小时的模型相比,批大小较大时模型需要训练更多的 epoch 准确率才能达到了 98%。在本节模型中,刚开始的训练阶段,模型准确率相对较低,并且只有在运行了相当多的 epoch 后模型的准确率才能达到较高水平。其原因是,批大小较小时,在每个 epoch 中权重更新的次数要少得多。
数据集总大小为 60000,当我们以批大小为 4096 运行模型 500 个 epoch 时,权重更新进行了 500 × ( 60000 ÷ 4096 ) = 7000 500\times(60000\div4096)= 7000 500×(60000÷4096)=7000 次。当批大小为 64 时,权重更新进行了 500 × ( 60000 ÷ 32 ) = 468500 500\times(60000\div32)=468500 500×(60000÷32)=468500 次。因此,批大小越小,权重更新的次数就越多,并且通常在 epoch 数相同的情况下,准确率越好。同时,应注意批大小也不能过小,这可能导致训练时间过长以及过拟合情况的出现。
4. 构建深度神经网络提高模型准确性
到目前为止,我们使用的神经网络在输入层和输出层之间只有一个隐藏层。在本节中,我们将学习在神经网络中使用多个隐藏层(因此称为深度神经网络)以探究网络深度对模型性能的影响。
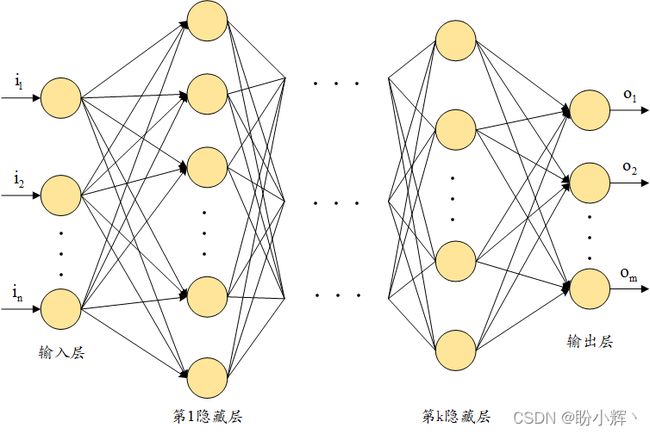
深度神经网络意味着在输入层和输出层间存在多个隐藏层。多个隐藏层确保神经网络可以学习输入和输出之间的复杂非线性关系,而简单的神经网络则无法完成这样的需求。经典深度神经网络架构如下所示:
通过在输入和输出层之间添加多个隐藏层来构建深度神经网络架构,步骤如下所示。
- 加载数据集并对数据集进行缩放:
(x_train, y_train), (x_test, y_test) = mnist.load_data()
num_pixels = x_train.shape[1] * x_train.shape[2]
x_train = x_train.reshape(-1, num_pixels).astype('float32')
x_test = x_test.reshape(-1, num_pixels).astype('float32')
x_train = x_train / 255.
x_test = x_test / 255.
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_test.shape[1]
- 在输入和输出层之间使用多个隐藏层构建模型:
model = Sequential()
model.add(Dense(512, input_dim=num_pixels, activation='relu'))
model.add(Dense(1024, activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
模型体系结构的相关模型信息,如下所示:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 512) 401920
_________________________________________________________________
dense_1 (Dense) (None, 1024) 525312
_________________________________________________________________
dense_2 (Dense) (None, 64) 65600
_________________________________________________________________
dense_3 (Dense) (None, 10) 650
=================================================================
Total params: 993,482
Trainable params: 993,482
Non-trainable params: 0
_________________________________________________________________
由于深度神经网络架构中包含更多的隐藏层,因此模型中也包含更多的参数。
- 建立了模型之后,就可以编译并拟合模型:
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=64,
verbose=1)
训练完成的模型的准确度约为 98.9%,比之前所用模型架构所得到的精确度略好,这是由于 MNIST 数据集相对简单。训练和测试损失及准确率如下:
在上图中可以看到,训练数据集准确率在很大程度上优于测试数据集准确率,这表明深度神经网络对训练数据进行了过度拟合。在之后的学习中,我们将了解避免训练数据过拟合的方法。
5. 学习率对网络性能的影响
在先前的模型中,我们一直使用 Adam 优化器,默认学习率为 0.0001。在本节中,手动将学习率设置为更高的数值,并查看更改学习率对模型准确率的影响,使用与先前示例相同的 MNIST 数据集。
在《神经网络基础》中,我们了解了学习率可以用于更新权重,权重的变化与减少的损失成正比。且权重值的变化等于损失的减少量乘以学习率。因此,学习率越低,权重值的变化越小,反之亦然。
本质上,可以将权重值视为一个连续的空间状态,其中权重是随机初始化的。当权重值的变化很大时,并不能充分的搜索到空间中的大量权重值。但是,当权重值的变化很小时,权重可能会达到全局最小值,因为可以考虑更多可能的权重值:
5.1 基础示例
为了进一步理解这一点,我们拟合简单函数 y = 2 x y = 2x y=2x,其中初始权重值为 1.477,初始偏置值为 0。前向和后向传播过程与《神经网络基础》中的相同:
def feed_forward(inputs, outputs, weights):
hidden = np.dot(inputs, weights[0])
out = hidden + weights[1]
squared_error = (np.square(out - outputs))
return squared_error
def update_weights(inputs, outputs, weights, epochs, lr):
for epoch in range(epochs):
org_loss = feed_forward(inputs, outputs, weights)
wts_tmp = deepcopy(weights)
wts_tmp2 = deepcopy(weights)
for ix, wt in enumerate(weights):
# print(ix, wt)
wts_tmp[ix] += 0.0001
loss = feed_forward(inputs, outputs, wts_tmp)
del_loss = np.sum(org_loss - loss) / (0.0001 * len(inputs))
wts_tmp2[ix] += del_loss * lr
wts_tmp = deepcopy(weights)
weights = deepcopy(wts_tmp2)
return wts_tmp2
与在《神经网络基础》中的反向传播函数相比,唯一的变化是我们将学习率( learning rate, lr )作为参数传递给它,统计在不同 epoch 内学习率为 0.01 时的权重值的变化:
x = np.array([[1], [2], [3], [4]])
y = np.array([[2], [4], [6], [8]])
w = np.array([[[1.477]], [[0]]])
w_val = []
b_val = []
for k in range(1000):
w_new, b_new = update_weights(x, y, w, (k+1), 0.5)
w_val.append(w_new[0])
b_val.append(b_new[0])
可以使用以下代码绘制不同 epoch 的权重变化情况:
plt.plot(w_val)
plt.title('Weight value over different epochs when learning rate is 0.01')
plt.xlabel('epochs')
plt.ylabel('weight value')
plt.show()
绘制结果输出如下:
以类似的方式,绘制当学习率为 0.1 时,在不同 epoch 上的权重值如下:
下图显示了学习率为 0.5 时不同 epoch 的权重值:
观察以上情况,可以看到权重值最初都发生了巨大变化,并且学习率为 0.1 时模型仍可以收敛,而学习率为 0.5 时没有收敛到最优解,其陷入了局部最小值,因此无法达到最佳值 2。
5.2 MNIST 数据集上不同学习率对性能的影响
我们已经了解了学习率对模型的影响,接下来我们来看一下学习率对 MNIST 数据集上训练的模型影响,在该模型中,我们使用与之前相同的模型架构,仅更改学习率参数。
- 通过指定优化器来改变模型的学习率:
from keras import optimizers
# 以学习速率 `0.01` 初始化 `Adam` 优化器
adam = optimizers.Adam(lr=0.01)
- 按照以下方式构建,编译和拟合模型:
model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer=adam, metrics=['acc'])
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=64,
verbose=1)
在 50 个 epoch 结束时,网络的准确性约为 91%,观察损失值和准确率在不同 epoch 之间如何变化:
当学习率较高时,损失的下降较不平稳,低学习率模型会缓慢更新权重,从而导致平滑的减少损失值并获得较高的准确率。或者也可以说,当学习率较高时,损失值的跳跃变化是由于损失值陷入局部最小值导致的。较低的学习率可以更好地达到最佳权重值,因为权重在正确的方向上缓慢但稳定地变化。
我们可以以类似的方式探索学习率高达 0.1 时的网络准确率:
from keras import optimizers
adam=optimizers.Adam(lr=0.1)
model = Sequential()
model.add(Dense(1000, input_dim=784, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer=adam, metrics=['accuracy'])
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=64,
verbose=1)
由于学习率高,损失值无法进一步降低,权重可能停留在局部最小值中:
因此,一般而言,将学习速率设置为较低的值并让网络在大量时间内进行训练是一种常用策略。
6. 不同损失优化器对模型性能的影响
在前面的模型中,我们设定损失优化器为 Adam 优化器。但是,优化器还有其他多种类型,优化器中的更改可能会影响模型学习拟合输入和输出的速度。在本节中,将了解更改优化器对模型准确性的影响。
为了了解更改优化器对网络准确性的影响,我们将前几节中的 Adam 优化器与本节中使用随机梯度下降优化器进行对比:
model = Sequential()
model.add(Dense(1000, input_dim=num_pixels, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['acc'])
history = model.fit(x_train, y_train,
validation_data=(x_test, y_test),
epochs=50,
batch_size=64,
verbose=1)
当我们使用随机梯度下降优化器时,在 50 个 epoch 之后的最终精度约为 98%:
但是,与使用 Adam 优化器的模型相比,该模型获得较高准确率的速度要慢得多。其他一些可用的损失优化器如下:
- RMSprop
- Adagrad
- Adadelta
- Adamax
- Nadam
小结
在本文中,学习了数据预处理、批大小和网络深度等多种因素在网络训练中的重要作用,并研究了如何通过使用不同的超参数来优化神经网络性能,充分发挥神经网络模型的拟合能力;并且初步了解了过拟合对模型的不利影响。
系列链接
Keras深度学习实战(1)——神经网络基础与模型训练过程详解
Keras深度学习实战(2)——使用Keras构建神经网络