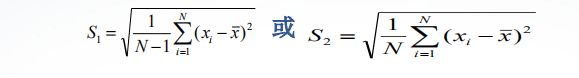MATlab--建模篇

1 数据统计分析

1. 求矩阵的最大元素和最小元素
    max()：求向量或矩阵的最大元素。
    min()：求向量或矩阵的最小元素。

（1）y=max(X)：返回向量X的最大值存入y，如果X中包含复数元素，则按模取最大值。
（2）[y,k]=max(X)：返回向量X的最大值存入y，最大值元素的序号存入k，如果X中包含复数元素，则按模取最大值。

矩阵

（1）max(A)：返回一个行向量，向量的第i个元素是矩阵A的第i列上的最 大值。
（2）[Y,U]=max(A)：返回行向量Y和U，Y向量记录A中每列的最大值，U向 量记录每列最大值元素的行号。
（3）max(A,[],dim)：dim取1或2。dim取1时，该函数的功能和max(A)完全
相同；dim取2时，该函数返回一个列向量，其第i个元素是A矩阵的第i行上 的最大值

在MATLAB中，求平均值和中值的函数分别为：
 mean()：求算术平均值。
 median()：求中值

3. 求和与求积
4. 累加和与累乘积
    sum():求和函数。
    prod():求积函数。
    cumsum():累加和函数。
    cumprod():累乘积函数。

（1）std(X)：计算向量X的标准差。
（2）std(A)：计算矩阵A的各列的标准差。

（3）std(A,flag,dim)： flag取0或1，当flag=0时，按S1所列公式计算样本标准方差；当flag=1时，按S2所列公式计算总体标准方差。在默
认情况下，flag=0，dim=1。

排序

排序函数为sort()，其调用格式为：
（1）sort(X)：对向量X按升序排列。
（2）[Y,I]=sort(A,dim,mode)，
其中dim指明对A的列还是行进行排序。
mode指明按升序还是降序排序，
若取“ascend”，则按升序；
若取“descend”，
则按降序，默认为升序。
输出参数中，Y是排序后的矩阵，而I记录Y中的元素在A中位置

相关系数能够反映两组数据序列之间相互关系，其计算公式为

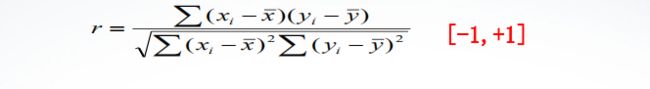
corrcoef()，其调用格式为：
（1）corrcoef(A)：返回由矩阵A所形成的一个相关系数矩阵，其中，第i行第j
列的元素表示原矩阵A中第i列和第j列的相关系数。
（2）corrcoef(X,Y)：在这里，X,Y是向量，它们与corrcoef([X,Y])的作用一
样，用于求X、Y向量之间的相关系数。

2 多项式计算

p(x)表示为向量形式：

conv(P1,P2)：多项式相乘，其中，P1、P2是两个多项式系数向量。

[Q,r]=deconv(P1,P2)：多项式相除，其中Q返回多项式P1除以P2的商式，r返 回P1除以P2的余式。这里，Q和r仍是多项式系数向量。deconv是conv的逆函
数，因此有下式成立。
P1=conv(Q,P2)+r

多项式系数向量包含0次项系数，所以其长度为多项式最高次数加1。

3. 多项式的求导
在MATLAB中，多项式求导函数为polyder()，其调用格式为：
（1）p=polyder ( P)：求多项式P的导函数。
（2）p=polyder(P,Q)：求P×Q的导函数。
（3）[p,q]=polyder(P,Q)：求P/Q的导函数，导函数的分子存入p，分母存入q

4. 多项式的求值
 polyval(p,x)：代数多项式求值，其中，p为多项式系数向量，x可以
是标量、向量或矩阵。若x为标量，则求多项式在该点的值；若x为向
量或矩阵，则对向量或矩阵中的每个元素求多项式的值。
 polyvalm(p,x)：矩阵多项式求值，其调用格式与polyval相同，但含
义不同。polyvalm函数要求x为方阵，以方阵为自变量求多项式的值

5. 多项式的求根
在MATLAB中，多项式求根函数为roots ( p )，其中p为多项式的系数向量。

3 数据插值

从数学上来说，数据插值是一种函数逼近的方法。

在MATLAB中，一维插值函数为interp1()，其调用格式为：
Y1=interp1(X,Y,X1,method)
该语句将根据X、Y的值，计算函数在X1处的值。其中，X、Y是两个等长的已知向量，分别表示采样点和采样值。X1是一个向量或标量，表示要-插值的点

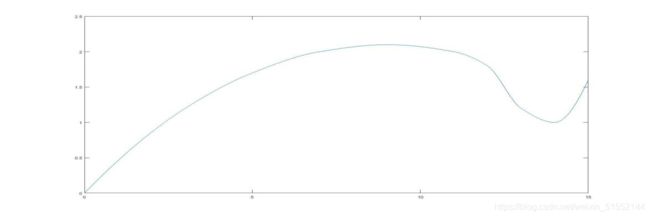
>> x=[0,3,5,7,9,11,12,13,14,15];
>> y=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
>> x1=0:0.1:15;
>> y1=interp1(x,y,x1,'spline');
>> plot(x1,y1)

method参数用于指定插值方法，常用的取值有以下四种：

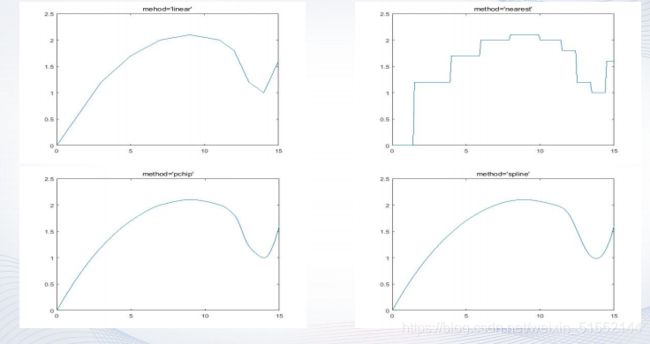
• （1）linear：线性插值，默认方法。将与插值点靠近的两个数据点用直线连接，然后在直线上选取对应插值点的数据。
• （2）nearest：最近点插值。选择最近样本点的值作为插值数据。
• （3）pchip：分段3次埃尔米特插值。采用分段三次多项式，除满足插值条 件，还需满足在若干节点处相邻段插值函数的一阶导数相等，使得曲线光 滑的同时，还具有保形性。
• （4）spline：3次样条插值。每个分段内构造一个三次多项式，使其插值 函数除满足插值条件外，还要求在各节点处具有连续的一阶和二阶导数。
  
  MATLAB中的二维插值函数为interp2()，其调用格式为：
  Z1=interp2(X,Y,Z,X1,Y1,method)

其中，X、Y是两个向量，表示两个参数的采样点，Z是采样点对应的函数值。X1、Y1是两个标量或向量，表示要插值的点。

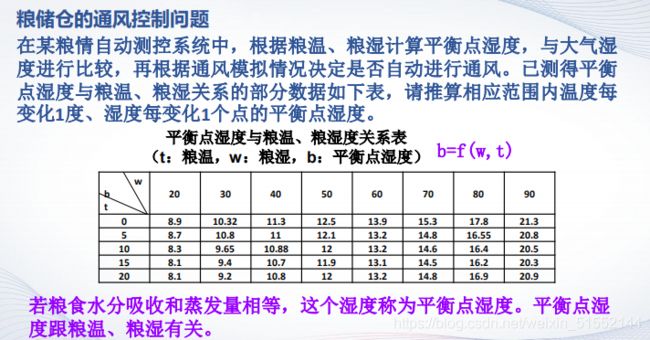
>> x=20:10:90;
>> y=(0:5:20)';
>> z=[8.9,10.32,11.3,12.5,13.9,15.3,17.8,21.3;
8.7,10.8,11,12.1,13.2,14.8,16.55,20.8;
8.3,9.65,10.88,12,13.2,14.6,16.4,20.5;
8.1,9.4,10.7,11.9,13.1,14.5,16.2,20.3;
8.1,9.2,10.8,12,13.2,14.8,16.9,20.9];
>> xi=20:90;
>> yi=(0:20)';
>> zi=interp2(x,y,z,xi,yi,'spline');
>> surf(xi,yi,zi)

4 数据插值应用举例

存在的问题是，d2是v的函数，但是函数关系未知，方程不可解。
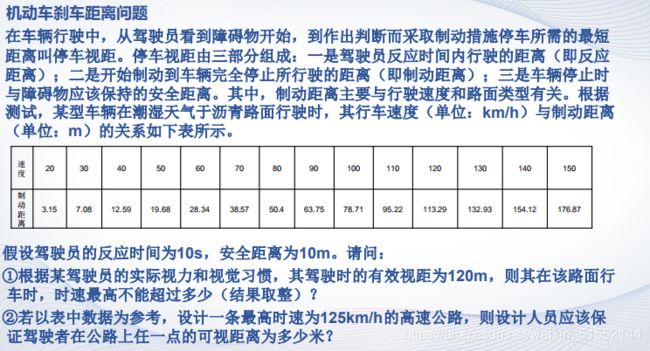
下面考虑数据插值方法，以表格中的数据为样本，进行数据插值，计算出与120m的停车视距所对应的速度指标。

编程思路：
第一步：建立速度和停车视距向量。
第二步：以1为单位，对采样区间内所有速度进行插值，计算出相应的停车视距。
第三步：求出停车视距120所对应的速度。
第四步：绘图展示。

 v=20:10:150;
vs=v.*(1000/3600);
d1=10.*vs;
d2=[3.15,7.08,12.59,19.68,28.34,38.57,50.4,63.75,
78.71,95.22,113.29,132.93,154.12,176.87];
d3=10;
d=d1+d2+d3;
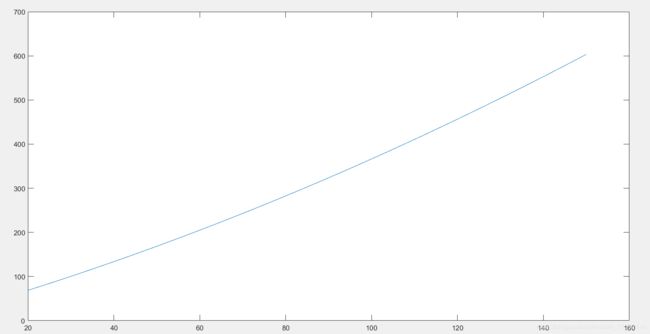
vi=20:1:150;
di=interp1(v,d,vi,'spline');  ##拟合曲线

如何根据停车视距120找到对应的速度？

• 第一步：令代表停车视距的向量di减去120，再取绝对值，得到一个新的向量x。
• 第二步：将x按升序排列，并记录最小元素的序号，该序号即为停车视距120所对 应的速度数据在向量vi中的序号。
• 第三步：根据序号取得速度数据

x=abs(di-120);
[y,i]=sort(x);
vi(i(1))
plot(vi,di,vi(i(1)),di(i(1)),'rp')

sort（）函数
sort将参量中的元素按升序或降序排列

eg: A=[1,5,3],则sort(A)=[1,3,5]
A=[1,5,3;2,4,1],则sort(A)=[1,4,1;2,5,3]

(2)B=sort(A,dim),对数组按指定方向进行升序排序,

• dim =1,表示对每一列进行排序
• dim=2表示对每一行进行排序.

(3)B=sort(A,dim,mode),mode为指定排序模式,

• mode为"ascend"时,进行升序排序,
• 为"descend "时,进行降序排序.

(4)[B,I]=sort(A,…),I为返回的排序后元素在原数组中的行位置或列位置.

如何根据停车视距120找到对应的速度？
第一步：令代表停车视距的向量di减去120，再取绝对值，得到一个新的向量x。
第二步：将x按升序排列，并记录最小元素的序号，该序号即为停车视距120所对
应的速度数据在向量vi中的序号。
第三步：根据序号取得速度数据。

x=abs(di-120);
[y,i]=sort(x);
vi(i(1))
plot(vi,di,vi(i(1)),di(i(1)),'rp')

第二问：

设计一条最高时速为125km/h的高速公路，则设计人员应该保证驾驶者在公路上任一点的可视距离为多少米？

>> j=find(vi==125);
>> di(j)
ans=
480.14
>> plot(vi,di,125,480.14,'rp')

沙盘制作问题

某地面部队分成红蓝两方在指定的陌生区域（平面区域[0,2000]*[0,2000]内，单位：m）进行作战演习。在演习过程中，红方侦查单位已经测得一些地点的高程如下表所示。

① 根据表中数据，制作军事沙盘。
② 在演习范围内，占领最大高地的一方将获得居高临下的优势。请问红方应第一时间抢占哪块区域

解题思路：

•  第一问：用二维插值估算数据，以方便制作军事沙盘。
•  第二问：在插值的基础上，绘制等高线图，找到最大高地。

x=0:200:1800;
y=x';
z=[2000,2000,2001,1992,1954,1938,1972,1995,1999,1999;
2000,2002,2006,1908,1533,1381,1728, 1959,1998,2000;
2000,2005,2043,1921,977,897,1310,1930,2003,2000;
1997,1978,2009,2463,2374,1445,1931,2209,2050,2003;
1992,1892,1566,1971,2768,2111,2653,2610,2121,2007;
1991,1875,1511,1556,2221,1986,2660,2601,2119,2007;
1996,1950,1797,2057,2849,2798,2608,2303,2052,2003;
1999,1999,2079,2685,3390,3384,2781,2165,2016,2000;
2000,2002,2043,2271,2668,2668,2277,2049,2003,2000;
2000,2000,2004,2027,2067,2067,2027,2004,2000,2000];
surf(x,y,z);

x1=0:100:1800;
y1=x1';
z1=interp2(x,y,z,x1,y1,'spline');
surf(x1,y1,z1);
x2=0:50:1800;
y2=x2';
z2=interp2(x1,y1,z1,x2,y2,'spline');
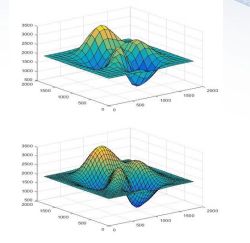
surf(x2,y2,z2);

contour(x2,y2,z2,12)  // 等高线

5.5 曲线拟合

引例-人口预测问题
人口增长是当今世界上都关注的问题，对人口增长趋势进行预测是各国普遍的做法。已知某国1790年到2010年间历次人口普查数据如下表所示，请预测该国2020年的人口数。

解题思路：找一个函数，去逼近这些数据，然后再根据找到的函数，计算预测点的值

x=1790:10:2010;
y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,63.0,76.0,92.0,
105.7,122.8,131.7,150.7,179.3,203.2,226.5,248.7,281.4,308.7];
plot(x,y,'*');
p=polyfit(x,y,3);  ##拟合三次
polyval(p,2020)    ##预测2020
plot(x,y,'*',x,polyval(p,x))

p = polyfit(x,y,n);
% 其中x,y表示需要拟合的坐标点，大小需要一样； n表示多项式拟合的次数。
% 返回值p表示多项式拟合的系数，系数从高到低排列

两个问题：

•  （1）用什么类型的函数做逼近函数？多项式函数
•  （2）误差最小到底怎么计算？最小二乘法

曲线拟合的实现方法
MATLAB中的多项式拟合函数为polyfit()，其功能为求得最小二乘拟合多项式系数，其调用格式为：

• （1）P=polyfit(X,Y,m)
• （2）[P,S]=polyfit(X,Y,m)

还返回一个结构体 S，后者可用作 polyval 的输入来获取误差估计值。

• （3）[P,S,mu]=polyfit(X,Y,m)

根据样本数据X和Y，产生一个m次多项式P及
其在采样点误差数据S，mu是一个二元向量，mu(1)是mean(X)，而mu(2)是std(X)。

问题分析：

据研究，一个国家的人口增长具有如下特点：
（1）发展越平稳，人口增长越有规律。 （2）当经济发展到一定水平时，人口增长率反而下降。
换言之，在不同的环境和经济发展水平，人口可能有不同的增长规律。

结论： 在人口增长数据的拟合上，应该将二战后至今这一时期的数据与此前的数据分 开处理。

5.6 曲线拟合应用举例

 股票预测问题
 算法的参数优化问题

股票预测问题
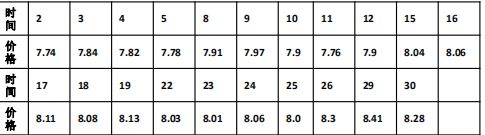
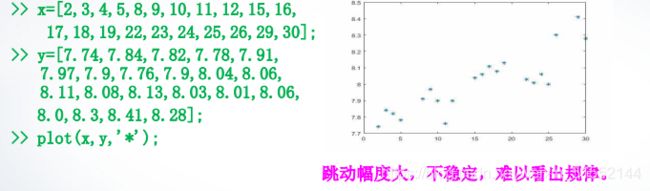
已知一只股票在2016年8月每个交易日的收盘价如下表所示，试预测其后面的大体走势

plot是画图函数
polyval是求值函数
polyfit是曲线拟合函数
polyfit用于多项式曲线拟合
p=polyfit(x,y,m)

其中, x, y为已知数据点向量, 分别表示横,纵坐标, m为拟合多项式的次数, 结果返回m次拟合多项式系数, 从高次到低次存放在向量p中.
y0=polyval(p,x0)
可求得多项式在x0处的值y0

• y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。
• [y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。则Y DELTA将至少包含50%的预测值。

常见运算

因式分解,展开，合并，简化，通分

expand(f)

绘图

二维数据曲线图

绘制二维曲线的基本函数

plot()函数

t=0:0.1:2*pi; 
x=2 * t; 
y=t.*sin(t).*sin(t); 
plot(x, y);

含多个输入参数的plot函数

plot函数可以包含若干组向量对，每一组可以绘制出一条曲线。含多个输入参数的plot函数调用格式为：plot(x1，y1，x2，y2，…，xn，yn)

x=linspace(0,2*pi,100);
plot(x,sin(x),x,2*sin(x),x,3*sin(x))

含选项的plot函数

例: 利用五角星标记例两曲线的交叉点

% 横坐标轴 
x = linspace(0, 2*pi, 1000); 
% 生成数据点，纵坐标轴 
y1 = 0.2 * exp(-0.5 * x).* cos(4 * pi * x); 
y2 = 2 * exp(-0.5 * x) .* cos(pi * x); 
% 查找y1与y2相等点（近似相等）的下标 
k = find( abs(y1-y2) < 1e-2 );  
%取y1与y2相等点的x坐标 
x1 = x(k);  
% 求y1与y2值相等点的y坐标 
y3 = 0.2 * exp(-0.5 * x1) .* cos(4 * pi * x1);  
% 绘图 
figure 
plot(x, y1, 'r-.', x, y2, 'k:', x1, y3, 'bp','LineWidth',2); 

双纵坐标函数plotyy

plotyy(x1,y1,x2,y2)

x1,y1对应一条曲线，x2,y2对应另一条曲线。横坐标的标度相同，纵坐标有两个，左边的对应x1,y1数据对，右边的对应x2,y2。

需要再专研

绘制图形的辅助操作

图形标注

title（’图形名称’）
xlabel（’x轴说明’）
ylabel（’y轴说明’）
text（x，y，’图形说明’）
legend（’图例1’，’图例2’，…）

坐标控制

axis（[xmin xmax ymin ymax zmin zmax]）
如果只给出前四个参数，则按照给出的x、y轴的最小值和最大值选择坐标系范围，绘制出合适的二维曲线。如果给出了全部参数，则绘制出三维图形。
axis函数的功能丰富，其常用的用法有：
axis equal：纵横坐标轴采用等长刻度
axis square：产生正方形坐标系（默认为矩形）
axis auto：使用默认设置
axis off：取消坐标轴
axis on：显示坐标轴
axis tight：按紧凑方式显示坐标轴范围，即坐标轴范围为绘图数据的范围
grid on/off：命令控制画还是不画网格线