Python数据分析大杀器之Numpy详解
Python数据分析
- 个人主页:JoJo的数据分析历险记
- 个人介绍:小编大四统计在读,目前保研到统计学top3高校继续攻读统计研究生
- 如果文章对你有帮助,欢迎关注、点赞、收藏、订阅专栏
本专栏主要介绍python数据分析领域的应用
参考资料:
https://github.com/fengdu78/Data-Science-Notes
文章目录
- Python数据分析
- numpy 基础
-
- ️1.数组对象
- 2.使用numpy创建多维数组
- 3.多维数组数据类型
-
- 3.1 查看数据类型
- 3.2 转换数据类型
- 4.numpy数组运算
-
- 4.1 数组相加
- 4.2 数组减法
- 4.3 数组乘法
- 4.4 数组除法
- 4.5 数组比较
- 5.广播机制
- 6.基础索引和切片
- 7.布尔型索引
- ☘️8.花式索引
- 9.数组转置和纬度变换
- 10.numpy数学函数
- 11 线性代数
- 12.随机数生成
- ✨文章推荐
numpy 基础
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。在我们数据分析时,方便我们进行数据的基本处理,并且它的速度很快。本文介绍一下numpy的基础用法,如果想要全面的学习numpy,可以参考numpy官方文档
首先导入numpy包,如果没有需要提前安装
pip install numpy
import numpy as np
️1.数组对象
我们可以使用np.arange()函数创建数组对象
首先我们创建一个一维数组
arr1 = np.arange(10)
arr1
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
使用type()查看arr1的类型
type(arr1)
numpy.ndarray
可以看出arr1的数据类型是ndarry
下面再来查看一下这个数组纬度的个数,数组纬度,和数组个数以及数组元素的类型
arr1.ndim
1
说明是一维数组
arr1.shape
(10,)
说明数组是(10,)的
arr1.size
10
数组一共有十个元素
arr1.dtype
dtype('int32')
说明数组的元素都是int32类型的
2.使用numpy创建多维数组
上面我们介绍了数组对象的基本使用,在numpy中,有多重方式可以创建数组对象,上面我们使用了np.arange(),下面我们看一下如何使用其他方法创建多维数组
下面这个两个代码返回结果一样
arr2 = np.array([1,2,3])
arr3 = np.arange(1,4)
arr2 == arr3
array([ True, True, True])
创建二维数组
arr4 = np.array([[1,2,3],[4,5,6]])
arr4
array([[1, 2, 3],
[4, 5, 6]])
创建3*3的零数组
np.zeros((3,3))
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
创建一个3*3的1数组
np.ones((3,3))
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
创建一个3*3的单位阵
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
使用dtype参数在定义数组时定义元素类型
np.eye(3,dtype='float')
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
生成指定值的3*3数组
np.full((3,3),fill_value=5)
array([[5, 5, 5],
[5, 5, 5],
[5, 5, 5]])
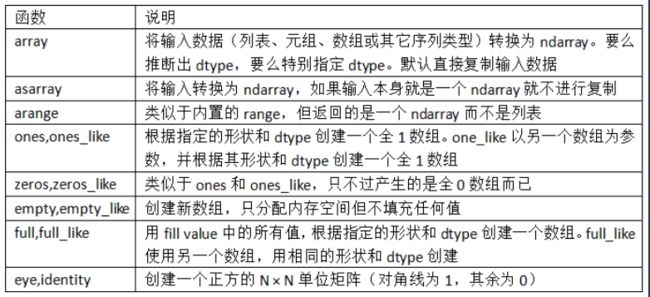
numpy定义数组的主要函数如下
3.多维数组数据类型
3.1 查看数据类型
n1 = np.array([[1,2,3],[4,5,6]])
n1.dtype
dtype('int32')
3.2 转换数据类型
n2 = n1.astype(np.float32)
n2
array([[1., 2., 3.],
[4., 5., 6.]], dtype=float32)
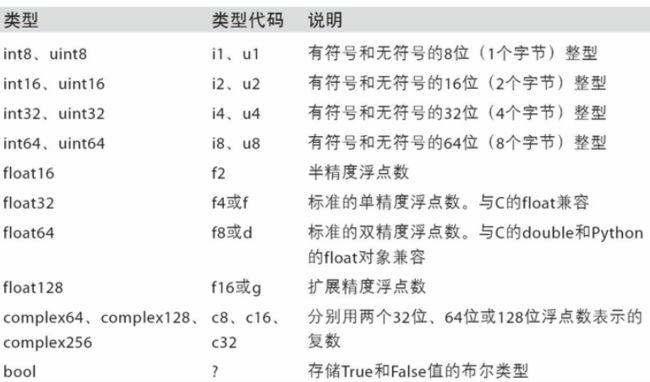
numpy中具体的数据类型如下
4.numpy数组运算
4.1 数组相加
n1 + n1
array([[ 2, 4, 6],
[ 8, 10, 12]])
4.2 数组减法
n1-n1
array([[0, 0, 0],
[0, 0, 0]])
4.3 数组乘法
使用*用于数组相乘,返回对应位置上的乘积
n1 * n1
array([[ 1, 4, 9],
[16, 25, 36]])
4.4 数组除法
n1 / n1
array([[1., 1., 1.],
[1., 1., 1.]])
4.5 数组比较
n3 = arr2 = np.array([[0.,4.,1.],[7.,2.,12,]])
n1>n3
array([[ True, False, True],
[False, True, False]])
5.广播机制
数组之间要想做加减乘除默认情况下要求纬度是相等的,但是numpy有一个技巧叫做广播机制,能根据数组纬度自动进行填充,我们先来看一个简单的例子
a = np.array([[0.0,0.0,0.0],[10.0,10.0,10.0],[20.0,20.0,20.0],[30.0,30.0,30.0]])
b = np.array([1.0,2.0,3.0])
print('第一个数组:')
print(a)
print('\n第二个数组:')
print(b)
print('\n第一个数组加第二个数组:')
print(a + b)
第一个数组:
[[ 0. 0. 0.]
[10. 10. 10.]
[20. 20. 20.]
[30. 30. 30.]]
第二个数组:
[1. 2. 3.]
第一个数组加第二个数组:
[[ 1. 2. 3.]
[11. 12. 13.]
[21. 22. 23.]
[31. 32. 33.]]
从上述结果可以看出,这两个数组的纬度并不相同,但是他们具有相同的列,此时,触发广播机制,第二个数组默认重复。其具体工作原理可以看一下下面这张图
注意:广播机制也不是任意两个数组都能触发的,例如下面这个例子
a = np.array([[0.0,0.0,0.0],[10.0,10.0,10.0],[20.0,20.0,20.0],[30.0,30.0,30.0]])
b = np.array([1.0,2.0])
a+b
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Input In [23], in | ()
1 a = np.array([[0.0,0.0,0.0],[10.0,10.0,10.0],[20.0,20.0,20.0],[30.0,30.0,30.0]])
2 b = np.array([1.0,2.0])
----> 3 a+b
ValueError: operands could not be broadcast together with shapes (4,3) (2,)
| 此时报错了,这是因为a数组是(4,3),b数组是(2,)
6.基础索引和切片
numpy索引是中返回某一个给定位置的元素,切片是返回一个数组形式
通过下面这张图具体看一下切片的原理
下面我们通过一些实际例子来说明如何使用切片和索引
arr = np.arange(10)
print(arr)
print(arr[5])#返回数组的第六个元素
print(arr[5:8])# 返回数组的第6,7,8个元素,并返回数组
print(arr[1:6:2])#返回索引为1-6的元素,以2为步长
[0 1 2 3 4 5 6 7 8 9]
5
[5 6 7]
[1 3 5]
上述我们可以看出numpy中基础索引和切片的使用方法,基本和python的list用法一样,
下面我们看一下在多维数组情况下是如何使用的
二维数组情况下索引返回一个一维数组,切片返回一个二维数组
arr2d = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]]) # 创建二维数组
arr2d[1]
array([4, 5, 6])
arr2d[1:3]
array([[4, 5, 6],
[7, 8, 9]])
三维数组情况下索引返回一个二维数组,切片返回一个三维数组
arr3d = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
arr3d[0]
array([[1, 2, 3],
[4, 5, 6]])
arr3d[0:1]
array([[[1, 2, 3],
[4, 5, 6]]])
7.布尔型索引
根据布尔型进行索引原则,如果是True,则选择,如果是False,则不选择
# 定义一个名字数据
names = np.array(['Bob','Joe','Will','Bob'])
data = np.array([[79, 88, 80], [89, 90, 92], [83, 78, 85], [78, 76, 80]])
#一个名字代表一行
print(names)
print(data)
['Bob' 'Joe' 'Will' 'Bob']
[[79 88 80]
[89 90 92]
[83 78 85]
[78 76 80]]
下面我们要返回名字是Bob的行
names == 'Bob'
array([ True, False, False, True])
首先得到了一个布尔型数组,我们通过这个布尔型进行索引
data[names=='Bob']
array([[79, 88, 80],
[78, 76, 80]])
发现结果返回第一行和最后一行,刚好对应Bob对应的位置
☘️8.花式索引
基本思想是利用整数数组进行索引
# 首先生成一个二维数组
arr = np.arange(32).reshape((8,4))
arr
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31]])
下面我们先传入单个索引数组,如下所示
arr[[4,3,0,6]]
array([[16, 17, 18, 19],
[12, 13, 14, 15],
[ 0, 1, 2, 3],
[24, 25, 26, 27]])
结果一次性返回索引为[4,3,0,6]组合的二维数组
#一次传入多个索引数组会有一点特别。它返回的是一个一维数组,其中的元素对应各个索引元元素
# 例如返回(1,0),(5,3)的元素
arr[[1,5],[0,3]]
array([ 4, 23])
9.数组转置和纬度变换
在进行矩阵运算时候,例如在神经网络中计算前向传播和反向传播时,经常要用到矩阵的转置,下面我们来看一下如何使用numpy进行转置
# 生成一个二维数组
arr = np.arange(12).reshape(3, 4)
使用T方法可以直接进行转置
arr.T
array([[ 0, 4, 8],
[ 1, 5, 9],
[ 2, 6, 10],
[ 3, 7, 11]])
使用reshape方法进行纬度转换
arr = np.arange(16).reshape((2, 2, 4))
arr
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
使用Transpose方法进行转置
arr.transpose(1, 2,0)
array([[[ 0, 8],
[ 1, 9],
[ 2, 10],
[ 3, 11]],
[[ 4, 12],
[ 5, 13],
[ 6, 14],
[ 7, 15]]])
10.numpy数学函数
arr = np.array([1,2,3])
求平方
np.square(arr)
array([1, 4, 9], dtype=int32)
开方
np.sqrt(arr)
array([1. , 1.41421356, 1.73205081])
11 线性代数
numpy中还有许多关于线性代数的函数,具体如下:
x = np.array([[1,2,3],[4,5,6]])
y = np.array([[1,2],[4,5],[5,8]])
矩阵相乘
np.dot(x,y)
array([[24, 36],
[54, 81]])
from numpy.linalg import inv,qr
求矩阵的逆
x = np.array([[1,2,3],[4,5,6],[7,8,9]])
inv(x)
array([[ 3.15251974e+15, -6.30503948e+15, 3.15251974e+15],
[-6.30503948e+15, 1.26100790e+16, -6.30503948e+15],
[ 3.15251974e+15, -6.30503948e+15, 3.15251974e+15]])
求矩阵特征根矩阵
qr(x)
(array([[-0.12309149, 0.90453403, 0.40824829],
[-0.49236596, 0.30151134, -0.81649658],
[-0.86164044, -0.30151134, 0.40824829]]),
array([[-8.12403840e+00, -9.60113630e+00, -1.10782342e+01],
[ 0.00000000e+00, 9.04534034e-01, 1.80906807e+00],
[ 0.00000000e+00, 0.00000000e+00, -1.11164740e-15]]))
12.随机数生成
使用np.random模块生成随机数,每一次结果都不同,为了代码的可复现性,可以设置随机种子
np.random.rand(3, 3) # 随机生成一个二维数组
array([[0.5488135 , 0.71518937, 0.60276338],
[0.54488318, 0.4236548 , 0.64589411],
[0.43758721, 0.891773 , 0.96366276]])
np.random.rand(2, 3, 3) # 随机生成一个三维数组
array([[[0.38344152, 0.79172504, 0.52889492],
[0.56804456, 0.92559664, 0.07103606],
[0.0871293 , 0.0202184 , 0.83261985]],
[[0.77815675, 0.87001215, 0.97861834],
[0.79915856, 0.46147936, 0.78052918],
[0.11827443, 0.63992102, 0.14335329]]])
np.random.seed(0)
np.random.rand(4) # 生成随机数种子
array([0.5488135 , 0.71518937, 0.60276338, 0.54488318])
np.random.seed(0)
np.random.rand(4)
array([0.5488135 , 0.71518937, 0.60276338, 0.54488318])
可以看出当我们设定好随机数种子之后,生成的随机数是一致的
✨文章推荐
Python数据可视化大杀器之Seaborn:学完可实现90%数据分析绘图
大家如果想要Numpy100题题目和答案可以在评论区留言!