【论文学习】《Adversarial examples for generative models》
《Adversarial examples for generative models》论文学习
文章目录
- 《Adversarial examples for generative models》论文学习
-
- 摘要
- 1 介绍
- 2 相关工作与背景
-
- 2.1 关于对抗的相关工作
- 2.2 VAE和VAE-GAN的背景
- 3 问题定义
-
- 3.1 激励攻击场景
- 3.2 用生成模型定义对抗样本
- 4 攻击方法
-
- 4.1 分类器攻击
- 4.2 L V A E \mathcal{L}_{VAE} LVAE攻击
- 4.3 潜在空间攻击
- 4.4 对抗优化问题的求解方法
- 4.5 测量攻击效果
- 5 评估
-
- 5.1 MNIST
-
- 5.1.1 分类器攻击
- 5.1.2 L V A E \mathcal{L}_{VAE} LVAE 攻击
- 5.1.3 潜在空间攻击
- 5.2 SVHN
- 5.3 CELEBA
- 5.4 不同攻击方法的总结
- 6 结论
摘要
我们探讨了在诸如变分自编码器(VAE)和VAE-GAN等深层生成模型上生成对抗实例的方法。众所周知,深度学习体系结构容易受到对抗示例的攻击,但之前的工作主要集中在对抗示例在分类任务中的应用。由于能够对输入数据分布进行建模并从这些分布生成真实的示例,深度生成模型最近变得流行起来。我们提出了针对VAE和VAE-GAN体系结构的三种攻击,并对在MNIST、SVHN和CelebA上训练的网络进行了演示。我们的第一次攻击利用基于分类的对手,将分类器附加到目标生成模型的训练有素的编码器上,然后可以使用该编码器间接操纵潜在的表示。我们的第二次攻击直接使用VAE损失函数从对抗实例生成目标重建图像。我们的第三次攻击超越了依赖分类或梯度的标准损失,而是直接针对源和目标潜在表现的差异进行优化。我们还解释了为什么攻击者可能对在目标生成网络上部署此类技术感兴趣。
1 介绍
对抗样本已经被证明存在于各种深度学习架构中它们是原始输入的微小扰动,通常人类观察者几乎看不到,但经过精心设计,可以误导网络产生不正确的输出。Szegedy等人(《Intriguing properties of neural networks》)和Goodfellow等人(《Explaining and Harnessing Adversarial Examples》)的开创性工作,以及许多最近的工作表明,对抗样本是丰富的,而且很容易找到它们。
以往的工作主要集中在对抗样本在分类任务中的应用上,深度网络将类别分配给输入图像。该攻击在原始输入图像上增加了小的对抗扰动。这些扰动导致网络改变输入的分类,从正确的类到其他不正确的类(可能是攻击者选择的)。关键的是,扰动输入必须仍然被人类观察者识别为属于原始输入类。
深层生成模型,如Kingma等人(《Auto-encoding variational bayes》),学习生成各种输出,从手写数字到人脸(《Deep convolutional inverse graphics network》),现实场景(《Conditional image generation with pixelcnn decoders》),视频(《Video pixel networks》), 3D对象(《Learning to generate chairs, tables and cars with convolutional networks》),和音频(《Wavenet: A generative model for raw audio》)。这些模型以不同的方式学习输入数据分布的近似值,然后从这个分布中进行抽样,生成之前未见过但貌似合理的输出。
据我们所知,之前没有研究过使用对抗输入来攻击生成模型。这样的工作有两个主要要求:描述攻击者可能想要攻击生成模型的可能场景;设计并演示一种攻击方式,可以成功对抗生成模型。我们在这项工作中处理了这两个要求。
生成模型最基本的应用之一是输入重构。给定一个输入图像,模型首先将其编码成一个低维的潜在表示,然后使用该表示生成原始输入图像的重构。由于潜在表示通常比原始输入的维数要少得多,因此可以将其用作一种压缩形式。潜表示也可以用来从输入中去除某些类型的噪声,即使在网络没有明确训练去噪的情况下,这是因为潜表示的低维限制了训练后的网络能够表示的信息。许多生成模型还允许通过采样不同的潜在值或修改潜在向量的单个维度来操纵生成的输出,而不需要经过编码步骤。
输入重构生成网络的这些特性表明,有效的对手可以对生成网络发动各种不同的攻击。任何针对潜在表示压缩瓶颈的攻击,都可能利用为使用潜在表示而构建的应用程序中的天然安全漏洞。具体地说,如果一个人做的编码解码步骤是分开的,攻击者可能会导致编码方相信他们已经为解码方编码了特定的信息,但实际上它们编码了攻击者选择的不同信息。我们更详细地探讨了这个想法,因为它适用于使用VAE或VAE-GAN架构压缩图像的应用。
2 相关工作与背景
本工作的重点是可变自动编码器(VAEs,由Kingma等人在《Auto-encoding variational bayes》中提出)和VAE-GANs(由Larsen等人在《Autoencoding beyond pixels using a learned similarity metric》中提出了由生成式对抗网络组成的VAEs)。
2.1 关于对抗的相关工作
现有文献中描述了许多针对分类模型的对抗攻击(《Explaining and Harnessing Adversarial Examples》,《Intriguing properties of neural networks》)。这些攻击可以是无目标的,其中对抗的目标是造成任何错误分类,或最不可能的错误分类(《Explaining and Harnessing Adversarial Examples》,《Adversarial examples in the physical world》);或者它们可以成为攻击者想要的特定错误分类的目标。Moosavi-Dezfooli等人(《Deepfool: a simple and accurate method to fool deep neural networks》)给出了一个强有力的有针对性的对抗攻击的最近示例。一些对抗攻击允许使用那些对目标模型本无访问权限的威胁模型(《Intriguing properties of neural networks》,《Practical black-box attacks against deep learning systems using adversarial examples》),但通常假定攻击者在在线或离线设置下确实有访问权限(《Intriguing properties of neural networks》)。
给定一个分类器 f ( x ) : x ∈ X → y ∈ Y f(x):x \in \mathcal{X} \to y \in \mathcal{Y} f(x):x∈X→y∈Y 和原始输入 x ∈ X x \in \mathcal{X} x∈X ,生成无目标对抗样本的问题可以表示为以下优化: a r g m i n x ∗ L ( x , x ∗ ) s . t . f ( x ∗ ) ≠ f ( x ) argmin_{x^*}L(x,x^*) \ s.t. \ f(x^*) \ne f(x) argminx∗L(x,x∗) s.t. f(x∗)=f(x) ,其中 L ( ⋅ ) L( \cdot ) L(⋅) 是输入空间的例子之间的距离度量(例如, L 2 L_2 L2范数)。类似地,对分类器生成有针对性的对抗攻击可以表示为 a r g m i n x ∗ L ( x , x ∗ ) s . t . f ( x ∗ ) = y t argmin_{x^*}L(x,x^*) \ s.t. \ f(x^*) = y_t argminx∗L(x,x∗) s.t. f(x∗)=yt ,其中 y t ∈ Y y_t \in \mathcal{Y} yt∈Y 是攻击者选择的某个目标标签。
这些优化问题通常可以用L-BFGS或Adam (《Adam: A method for stochastic optimization》),正如Szegedy等人(《Intriguing properties of neural networks》)和Carlini(《Towards evaluating the robustness of neural networks》)。它们也可以用单步梯度逼近技术,如快速梯度信号(《Explaining and harnessing adversarial examples》)、快速梯度 L 2 L_2 L2(《Learning with a strong adversary》)或快速最不可能类(《Adversarial examples in the physical world》);或者它们可以用这些方法的迭代变体和其他基于梯度的技术进行近似(《Adversarial examples in the physical world》,《Deepfool: a simple and accurate method to fool deep neural networks》)。
Sabour等人(《Adversarial manipulation of deep representations》)发现了这类攻击的一个有趣变体。在这项工作中,他们直接攻击目标网络的隐藏状态,方法是取得一个输入图像 x x x 和一个目标图像 x t x_t xt ,并搜索 x x x 的一个扰动变量,使其能在目标网络的第 l l l 层产生与 x t x_t xt 产生的同一层隐藏状态相似的隐藏状态。这种方法也可以直接应用于攻击生成模型的潜在向量。
在Tabacof等人(《Adversarial Images for Variational Autoencoders》)的并行工作中,这种攻击的一种变体也被应用到VAE模型中,该模型使用源图像和目标图像的潜在表示之间的KL散度来生成对抗样本。然而,在他们的论文中,作者提到,他们试图直接攻击输出,但这只会使重建更加模糊。虽然他们没有解释确切的实验设置,但攻击听起来与我们的 L V A E \mathcal{L}_{VAE} LVAE攻击相似,我们发现非常成功。此外,在他们的论文中,作者没有考虑更先进的VAE-GAN模型和更复杂的数据集,如CelebA。
2.2 VAE和VAE-GAN的背景
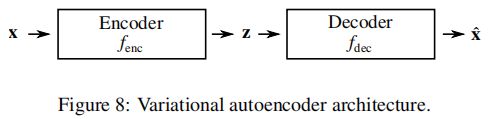
变分自动编码器的一般架构由三个组件组成,如图8所示。编码器 f e n c ( x ) f_{enc}(x) fenc(x) 是一个神经网络,它将高维输入表示 x x x 映射为低维(压缩)潜在表示 z z z 。所有 z z z 的可能值构成一个潜空间。在一个训练良好的VAE中,潜在空间中的相似值应该产生类似的解码器输出。最后,解码器/生成器 f d e c ( z ) f_{dec}(z) fdec(z),是一个神经网络,将压缩的潜在表示映射回高维输出 x ^ \hat{x} x^ 。组成这些网络可以进行基本的输入重构 x ^ = f d e c ( f e n c ( x ) ) \hat{x}=f_{dec}(f_{enc}(x)) x^=fdec(fenc(x))。这种组合架构在训练期间用于反向传播来自损失函数的错误。
变分自编码器的损失函数 L V A E \mathcal{L}_{VAE} LVAE 使网络能够学习一个潜在的表示,近似于棘手的后置分布 p ( z ∣ x ) p(z|x) p(z∣x) :
L V A E = − D K L [ q ( z ∣ x ) ∣ ∣ p ( z ) ] + E q [ l o g p ( x ∣ z ) ] (1) \mathcal{L}_{VAE}=-D_{KL}[q(z|x)||p(z)]+E_q[log \ p(x|z)] \tag{1} LVAE=−DKL[q(z∣x)∣∣p(z)]+Eq[log p(x∣z)](1) q ( z ∣ x ) q(z|x) q(z∣x)是所学的后验分布 p ( z ∣ x ) p(z|x) p(z∣x)的近似。 p ( z ) p(z) p(z)是潜在表示 z z z的先验分布。 D K L D_{KL} DKL表示Kullback Leibler散度。 E q [ l o g p ( x ∣ z ) ] E_q[log \ p(x|z)] Eq[log p(x∣z)]是变分下界,在输入重构的情况下是输入 x x x与其重构 x ^ \hat{x} x^之间的交叉熵 H [ x , x ^ ] H[x,\hat{x}] H[x,x^]。为了生成 x ^ \hat{x} x^,需要对 q ( z ∣ x ) q(z|x) q(z∣x)进行采样,然后计算 f d e c ( z ) f_{dec}(z) fdec(z)。
当从 q ( z ∣ x ) q(z|x) q(z∣x)采样时,要使VAE完全可微,需采用重参数化方法(《Auto-encoding variational bayes》)从网络中提取随机采样步长,并将其转化为输入 ε ε ε。高斯分布常被参数化。在本例中, f e n c ( x ) f_{enc}(x) fenc(x) 输出的是分布参数 μ \mu μ和 σ 2 σ^2 σ2。然后通过计算 z = μ + ε σ 2 z = \mu + ε \sqrt{σ^2} z=μ+εσ2 对该分布进行采样,其中 ε ∼ N ( 0 , 1 ) ε \sim N(0,1) ε∼N(0,1) 为输入随机样本,不依赖于 f e n c f_{enc} fenc的任何参数,因此不影响网络的差异化。
Larsen等人(《Autoencoding beyond pixels using a learned similarity metric》)的VAE-GAN体系结构具有与VAE相同的 f e n c f_{enc} fenc和 f d e c f_{dec} fdec对。它还添加了一个鉴别器 f d i s c f_{disc} fdisc,用于训练,就像在标准的生成式对抗网络中一样(《Generative Adversarial Networks》)。 f d e c f_{dec} fdec的损耗函数使用离散器损耗代替交叉熵来估计重构误差。
3 问题定义
我们为反对生成模型的对手提供了一个激励攻击场景,以及生成环境中对抗的正式定义。
3.1 激励攻击场景
为了激发下面介绍的攻击,我们描述了图1中描述的攻击场景。在这种情况下,有两方,发送方和接收方,他们希望通过计算机网络彼此共享图像。为了节省带宽,它们共享一个关于感兴趣的输入分布的VAE训练,这将允许它们只发送潜在向量 z z z。

攻击者的目标是说服发送方将攻击者选择的图像发送给接收方,但攻击者无法直接控制双方发送的字节数。然而,攻击者有一个共享的VAE的副本。攻击者向发送方呈现图像 x ∗ x^* x∗,它类似于发送方希望与接收方共享的图像 x x x。例如,发送方希望与接收方共享小猫的图片,因此攻击者向发送方呈现一个带有小猫图片的网络页面,小猫图片为 x ∗ x^* x∗。发送方选择 x ∗ x^* x∗,并将其对应的 z z z发送给接收方,接收方重新构建它。然而,由于攻击者控制了所选择的图像,当接收方重建它时,得到的不是 x x x的一个忠实的复制 x ^ \hat{x} x^,接收者看到攻击者选择的其他图像 x ^ a d v \hat{x}_{adv} x^adv,它与 x x x的含义不同(例如,向攻击者的银行账户汇款的请求)。
还有其他这种一般形式的攻击,在这种攻击中,发送方和接收方可能按距离分开(如本例中),或者按时间分开(如将压缩图像存储到磁盘以供以后检索)。在时间分离攻击中,发送者和接收者可能是同一个人,也可能是多个不同的人。在这两种情况下,如果他们使用的是VAE潜伏空间的不安全通道,那么他们共享的信息就有可能受到攻击者的控制。例如,如果自动监控系统在被其他系统处理之前使用这种压缩来存储视频信号,攻击者可能能够欺骗该系统。在这种情况下,对视频信号的后续分析可能会在泄露的数据上显示攻击者想要显示的内容。
虽然我们没有专门攻击他们的模型,但文献中已经提出了基于深度神经网络的可行压缩方案,显示了有希望的结果(《Variable rate image compression with recurrent neural networks》,《Full resolution image compression with recurrent neural networks.》)。
3.2 用生成模型定义对抗样本
我们对在目标生成模型 G t a r g ( x ) = f d e c ( f e n c ( x ) ) G_{targ}(x) = f_{dec}(f_{enc}(x)) Gtarg(x)=fdec(fenc(x)) 上生成对抗样本做如下假设。 G t a r g G_{targ} Gtarg在输入 X \mathcal{X} X 上进行训练,这些输入 X \mathcal{X} X 可以自然地用有语义意义的类 Y \mathcal{Y} Y 标记,尽管在训练时可能没有这样的标签,或者在训练期间可能没有使用这些标签。 G t a r g G_{targ} Gtarg通常在给出来自类 y y y 的输入 x x x 时,能成功生成一个类别为 y y y 的输出 x ^ = G t a r g ( x ) \hat{x} = G_{targ}(x) x^=Gtarg(x) 。换句话说,无论攻击者对什么目标输出类感兴趣,我们都假设 G t a r g G_{targ} Gtarg成功地在潜在表示中捕获了它,这样它就可以从解码器生成该类的示例。这个目标输出类不需要来自训练数据集中最显著的类。例如,在MNIST训练的模型上,攻击者可能不关心产生不同的目标数字(这是最显著的类别)。攻击者可能喜欢以不同的样式生成相同的输入数字(可能是为了帮助伪造)。我们还假设攻击者可以访问 G t a r g G_{targ} Gtarg。最后,攻击者可以访问与 X \mathcal{X} X 相同的分布中的一组示例,这些示例具有攻击者想要生成的目标标签 y t y_t yt 。这并不意味着攻击者需要访问标记过的训练数据集(可能不存在),或者访问一个适当的标记过的数据集,该数据集包含针对每个类 y ∈ Y y \in \mathcal{Y} y∈Y 标记的大量示例(这可能很难或收集成本高)。这里描述的攻击可能只需要标记为单个目标类的少量数据就能成功。
生成此类对手的一种方法是解决优化问题 a r g m i n x ∗ L ( x , x ∗ ) s . t . O R A C L E ( G t r a g ( x ∗ ) ) = y t argmin_{x^*} \ L(x, x^*) \ s.t. ORACLE(G_{trag}(x^*))=y_t argminx∗ L(x,x∗) s.t.ORACLE(Gtrag(x∗))=yt,其中 O R A C L E ORACLE ORACLE可靠地区分类 y t y_t yt和其他类的输入。在实践中,攻击者训练的分类器可以作为 O R A C L E ORACLE ORACLE。来自2.1节的其他类型的对手也可以用来以自然的方式近似这种优化,其中一些我们将在第4节中描述。
如果攻击者只需要生成一个成功的攻击,那么判断攻击是否成功的问题可以通过手动检查 x ∗ x^* x∗和 x ^ a d v \hat{x}_{adv} x^adv对并选择攻击者认为最好的一个来解决。但是,如果攻击者希望生成许多成功的攻击,则需要一种评估攻击成功程度的自动化方法。我们在4.5节中展示了如何使用训练在 z = f e n c ( x ) z = f_{enc}(x) z=fenc(x) 上的分类器自动测量攻击的有效性。
4 攻击方法
攻击者希望构造一个受对抗干扰的输入,以影响潜在的表示,从而导致重构过程为不同的类重构输出。我们提出了三种攻击生成模型的方法:一种基于分类器的攻击,我们在潜在空间 z z z上训练一个新的分类器,并使用该分类器在潜在空间中寻找对抗样本;使用 L V A E \mathcal{L}_{VAE} LVAE直接针对输出的攻击;攻击潜在空间 z z z。这三种方法在技术上都适用于任何依赖于习得的潜在表示 z z z的生成架构。在不丧失一般性的情况下,我们专注于VAE-GAN架构。
4.1 分类器攻击
通过在预训练的生成模型中加入分类器 f c l a s s f_{class} fclass,我们可以将生成模型的对抗生成问题转化为之前解决的为分类器生成对抗样本的问题。这种方法允许我们对文献中的分类器应用所有现有的攻击。然而,正如下面所讨论的,由于分类器的不准确性,使用这种分类器往往会从对抗样本中产生比其他两种攻击低质量的重建。
步骤1
冻结目标生成模型的权值,使用交叉熵等标准分类损失 L c l a s s i f i e r \mathcal{L}_{classifier} Lclassifier在 f e n c f_{enc} fenc之上训练一个新的分类器 f c l a s s ( z ) → y ^ f_{class}(z) \to \hat{y} fclass(z)→y^,如图3所示。这个过程与原始模型的训练方式无关,但它需要一个训练语料库,
该语料库与用于训练 G t a r g G_{targ} Gtarg的输入分布大致相同,并且至少有两个类带有真实值的标签: y t y_t yt和 y t ~ y_{\tilde{t}} yt~,两个相反的类。

步骤2
使用训练好的分类器,攻击者使用4.4节中描述的方法找到对抗样本 x ∗ x^* x∗。
使用 f c l a s s f_{class} fclass生成对抗样本并不总是导致高质量的重构,如图5和图11的中间列所示。这似乎是由于 f c l a s s f_{class} fclass给过程增加了额外的干扰。例如, f c l a s s f_{class} fclass有时会自信地错误分类那些远离训练数据分布的潜在向量 z z z,导致 f d e c f_{dec} fdec无法从对抗样本重建可靠的输出。


4.2 L V A E \mathcal{L}_{VAE} LVAE攻击
我们的第二种方法使用VAE损失函数产生对抗扰动。攻击者选择两个输入, x s x_s xs(源)和 x t x_t xt(目标),并使用一种标准的对抗方法将 x ^ s \hat{x}_s x^s扰动到 x ∗ x^* x∗中,使用章节4.4中描述的方法使其重构 x ∗ x^* x∗与 x t x_t xt的重构相匹配。
对抗在执行优化之前通过计算 f d e c ( f e n c ( x t ) ) f_{dec}(f_{enc}(x_t)) fdec(fenc(xt))一次来预计算重构 x ^ t \hat{x}_t x^t。为了在攻击中使用 L V A E \mathcal{L}_{VAE} LVAE,改变了 L V A E \mathcal{L}_{VAE} LVAE的第二项(重建损失)(见式1),不再计算 x x x与 x ^ \hat{x} x^之间的重建损失,而是计算 x ^ ∗ \hat{x}^* x^∗与 x ^ t \hat{x}_t x^t之间的损失。这意味着在每次优化迭代期间,对抗需要计算 x ^ ∗ \hat{x}^* x^∗,这需要计算完整的 f d e c ( f e n c ( x ∗ ) ) f_{dec}(f_{enc}(x^*)) fdec(fenc(x∗))。
4.3 潜在空间攻击
我们的第三种方法攻击生成模型的潜在空间。
单个潜在向量目标
这种攻击类似于Sabour等人(《Adversarial manipulation of deep representations》)的工作,他们使用一对源图像 x s x_s xs和目标图像 x t x_t xt生成 x ∗ x^* x∗诱发目标网络在一些隐藏层 l l l是产生类似于 x t x_t xt的激活,同时保持 x s x_s xs和 x ∗ x^* x∗之间的相似性。
为了使这种攻击作用于潜在生成模型,计算 z t = f e n c ( x t ) z_t = f_{enc}(x_t) zt=fenc(xt),然后使用下面的损失函数从不同的源图像 x s x_s xs中使用章节4.4中描述的方法生成对抗样本就足够了:
L l a t e n t = L ( z t , f e n c ( x ∗ ) ) (2) \mathcal{L}_{latent}=L(z_t,f_{enc}(x^*)) \tag{2} Llatent=L(zt,fenc(x∗))(2) L ( ⋅ ) L(·) L(⋅)是两个向量之间的距离。在潜在空间近似于欧氏的假设下,我们使用 L 2 L_2 L2范数。
4.4 对抗优化问题的求解方法
我们可以使用许多不同的方法来生成对抗样本。我们最初评估了Goodfellow等人(《Explaining and Harnessing Adversarial Examples》)的快速梯度信号方法和 L 2 L_2 L2优化方法。由于后者产生了更好的结果,我们关注于 L 2 L_2 L2优化方法,而我们在附录中包含了一些FGS结果。攻击既可以在目标模式下使用(在这种模式下,我们希望重构特定类 y t y_t yt),也可以在非目标模式下使用(在这种模式下,我们只希望重构不正确的类)。在本文中,我们重点研究攻击的目标模式。
L 2 L_2 L2优化:
基于优化的方法,Szegedy等人(《Intriguing properties of neural networks》2013)和Carlini等人(《Towards evaluating the robustness of neural networks》)将对抗性生成问题提出为以下优化问题:
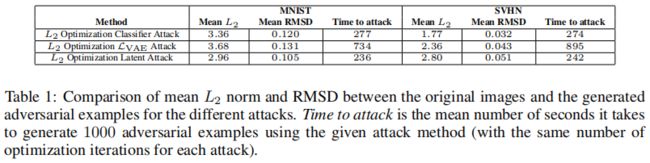
a r g m i n x ∗ λ L ( x , x ∗ ) + L ( x ∗ , y t ) (3) argmin_{x^*} \ \lambda L(x,x^*)+\mathcal{L}(x^*,y_t) \tag{3} argminx∗ λL(x,x∗)+L(x∗,yt)(3) 如上所示, L ( ⋅ ) L(·) L(⋅)是一个距离测度, L \mathcal{L} L是 L c l a s s i f i e r \mathcal{L}_{classifier} Lclassifier、 L V A E \mathcal{L}_{VAE} LVAE或 L l a t e n t \mathcal{L}_{latent} Llatent的一种。使用常数 λ \lambda λ来平衡这两个损失贡献。对于 L V A E \mathcal{L}_{VAE} LVAE攻击,优化器必须在优化器的每一步都进行完整的重构。另外两种攻击在优化器运行时不需要进行重构,因此它们可以更快地生成对抗样本,如表1所示。
4.5 测量攻击效果
为了根据生成模型自动生成大量的对抗样本,攻击者需要一种判断对抗样本质量的方法。我们利用类来估计特定的攻击是否成功。
重建反馈回路
该体系结构与图3所示相同。我们使用生成模型通过计算来重构尝试的对抗输入 x ∗ x^* x∗:
x ^ ∗ = f d e c ( f e n c ( x ∗ ) ) (4) \hat{x}^*=f_{dec}(f_{enc}(x^*)) \tag{4} x^∗=fdec(fenc(x∗))(4) 然后使用 f c l a s s f_{class} fclass进行计算:
y ^ = f c l a s s ( f e n c ( x ∗ ) ) (5) \hat{y}=f_{class}(f_{enc}(x^*)) \tag{5} y^=fclass(fenc(x∗))(5) 输入的对抗样本 x ∗ x^* x∗不直接分类,而是先输入生成模型进行重构。经我们检查,这个重建循环提高了分类器的准确率平均 60% 对抗攻击。将重构反馈回路后的预测标签 y ^ \hat{y} y^与攻击目标 y t y_t yt进行比较,判断对抗样本是否成功重构到目标类。如果 f c l a s s f_{class} fclass在 y t y_t yt上有足够高的查准率和召回率,那么 f c l a s s f_{class} fclass可以过滤掉大部分失败的对抗样本,同时保留大部分好的对抗样本。
我们从一个重构反馈循环后的分类器预测中得到两个度量。第一个度量是 A S i g n o r e − t a r g e t AS_{ignore-target} ASignore−target,即攻击成功率忽略目标,即不要求对抗样本的输出类与目标类匹配:
A S i g n o r e − t a r g e t = 1 N ∑ i = 1 N 1 y ^ i = y ^ (6) AS_{ignore-target}=\frac {1} {N} \sum^N_{i=1}\mathbf{1}_{\hat{y}^i = \hat{y}} \tag{6} ASignore−target=N1i=1∑N1y^i=y^(6) N N N是重建的对抗样本的总数;当图像 i i i的重建分类 y ^ i \hat{y}^i y^i不等于原图像的真实值分类 y i y^i yi时, 1 y ^ i ≠ y ^ \mathbf{1}_{\hat{y}^i \ne \hat{y}} 1y^i=y^为 1 1 1,否则为 0 0 0。第二个指标是 A S t a r g e t AS_{target} AStarget,即包含目标的攻击成功率(即要求对抗性样本的输出类与目标类匹配),我们将其定义为:
A S t a r g e t = 1 N ∑ i = 1 N 1 y ^ i ≠ y ^ (7) AS_{target}=\frac {1} {N} \sum^N_{i=1}\mathbf{1}_{\hat{y}^i \ne \hat{y}} \tag{7} AStarget=N1i=1∑N1y^i=y^(7) 对于更成功的攻击,这两个指标预计会更高。注意, A S t a r g e t ≤ A S i g n o r e − t a r g e t AS_{target} \le AS_{ignore-target} AStarget≤ASignore−target。在计算这些度量时,我们排除了与目标类具有相同基础真值类的输入样本。
5 评估
我们使用标准的训练和验证集分割来评估对MNIST (《Gradient-based learning applied to document recognition》)、SVHN (《Reading digits in natural images with unsupervised feature learning》)和CelebA (《Deep learning face attributes in the wild》)的三种攻击。VAE和VAE-GAN架构在TensorFlow (《TensorFlow: Large-scale machine learning on heterogeneous systems》)上实现。我们使用Adam对生成模型和分类器进行了优化,学习率为 0.001 0.001 0.001,其他参数设置为默认值。对于VAE,我们采用了两种架构:一个简单的架构,只有一个具有 512 512 512个单元的全连接隐藏层和ReLU激活功能;以及一种卷积架构,取自于最初Larsen等人的VAE-GAN论文(《Autoencoding beyond pixels using a learned similarity metric》)(但训练时只使用了VAE损失)。我们使用与VAE-GAN模型相同的经过额外GAN损失训练的体系结构,如该工作中所述。对于VAE和VAE-GAN,我们在MNIST上使用了 50 50 50维的潜在表征,在SVHN上使用了 1024 1024 1024维的潜在表征,在CelebA上使用了 2048 2048 2048维的潜在表征。
在本节中,我们只显示未从潜在空间中采样的结果。相反,我们使用均值向量 μ \mu μ作为潜在的表示 z z z。由于抽样会对最终的重建产生影响,我们分别对其进行评估。在大多数样本中,可见的变化很小,一般来说攻击仍然成功。
5.1 MNIST
尽管VAE-GAN的质量明显更好,但VAE和VAE-GAN都能自行重建原始输入,如图 9 9 9所示。作为对照,我们还生成了与对抗样本相同大小的随机噪声(见图 13 13 13),以表明随机噪声不会导致重构的噪声图像发生任何显著变化。虽然我们在VAEs和VAE-GANs上都进行了实验,但我们只显示了VAE-GAN的结果,因为它产生的重构质量比相应的VAE高得多。


5.1.1 分类器攻击
我们使用一个简单的分类器架构来帮助生成针对VAE和VAE-GAN模型的攻击。该分类器由两个全连接的隐藏层组成,每层 512 512 512个单元,使用ReLU激活函数。输出层是一个 10 10 10维的softmax。分类器的输入是由VAE/VAE-GAN编码器产生的 50 50 50维潜在表示。经过 100 100 100个周期的训练,该分类器在验证集上的准确率达到 98.05 % 98.05\% 98.05%。
为了查看类之间是否存在差异,我们为每个MNIST类生成有针对性的对抗样本,并给出每个类的结果。对于目标攻击,我们使用lambda 0.001 0.001 0.001的优化方法,其中基于Adam的优化对 1000 1000 1000个周期执行,学习率为 0.1 0.1 0.1。使用分类器攻击的原始图像与生成的对抗样本之间的差异的 L 2 L_2 L2范数平均值为 3.36 3.36 3.36,而RMSD平均值为 0.120 0.120 0.120。


表2中的数值结果表明,目标分类器攻击成功地欺骗了分类器。分类器的准确率降低到 0 % 0\% 0%,而匹配率(与目标类匹配的预测次数与错误分类的图像数量之比)为 100 % 100\% 100%,这意味着所有的错误预测都与目标类匹配。然而,我们感兴趣的(根据3.2节中的攻击定义)是生成式模型如何重建对抗样本。如果我们看一下由VAE-GAN生成的0类图像,如图4所示,目标攻击在一些重建图像上是成功的(例如,1、4、5、6和9被重建为0)。但即使分类器的准确率为 0 % 0\% 0%,匹配率为 100 % 100\% 100%,一个错误的分类并不一定会导致对目标类的重构,这表明分类器比生成式模型更容易被一个对抗样本所欺骗。

重建反馈回路
第4.5节中描述的重构反馈回路可以用来衡量目标攻击在多大程度上成功地使生成模型改变重构类。附录中的表4显示了所有源类和目标类对的 A S i g n o r e − t a r g e t AS_{ignore-target} ASignore−target和 A S t a r g e t AS_{target} AStarget。值越大表示对这对类的攻击越成功。有趣的是,观察到攻击某些源/目标对比其他的更容易(例如,对(4,0)vs.(0,8)),并且结果在源/目标对上是不对称的。同样,一些对在 A S i g n o r e − t a r g e t AS_{ignore-target} ASignore−target中表现良好,但在 A S t a r g e t AS_{target} AStarget中表现较差。如图11所示,针对4的分类器对抗样本始终无法重构出容易识别的4。大多数的重构看起来像5,但是源5的反向重构的样本看起来像0或3。
5.1.2 L V A E \mathcal{L}_{VAE} LVAE 攻击
为了使用 L V A E \mathcal{L}_{VAE} LVAE攻击生成对抗示例,我们使用了 λ = 1.0 λ = 1.0 λ=1.0的优化方法,其中基于Adma的优化执行了 1000 1000 1000个周期,学习率为 0.1 0.1 0.1。使用该方法,原始图像与生成的对抗样本之间的差异的 L 2 L_2 L2均值范数为 3.68 3.68 3.68,而均值RMSD为 0.131 0.131 0.131。

我们在附录中的表5中显示了 L V A E \mathcal{L}_{VAE} LVAE攻击的 A S i g n o r e − t a r g e t AS_{ignore-target} ASignore−target和 A S t a r g e t AS_{target} AStarget。对比潜在攻击的数值评估结果(下图)可以看出,两种方法在MNIST上都取得了相似的结果。
5.1.3 潜在空间攻击
为了使用潜在攻击生成对抗样本,我们使用了 λ = 1.0 λ = 1.0 λ=1.0的优化方法,其中基于Adam的优化执行了 1000 1000 1000个周期,学习率为 0.1 0.1 0.1。使用这种方法,原始图像和生成的对抗样本之间的差异的 L 2 L_2 L2均值范数为 2.96 2.96 2.96,而平均RMSD为 0.105 0.105 0.105。

表3显示了所有源和目标类对的 A S i g n o r e − t a r g e t AS_{ignore-target} ASignore−target和 A S t a r g e t AS_{target} AStarget。与分类器攻击的数值评估结果比较,可以看出潜在攻击的性能要好得多。当视觉上比较重建图像时,这个结果仍然是正确的,如图5所示。

我们还尝试了一种潜在攻击的非目标版本,其中我们改变公式2,使原始图像编码与对抗样本编码之间的潜在空间距离最大化。在这种情况下,我们试图最小化的损失是无界的,因为 L 2 L_2 L2 距离总是会变大,所以攻击通常无法产生一个合理的对抗样本。

此外,我们还试验了针对训练集中特定图像的潜在表示,而不是取均值,如第4.3节所述。我们在表3中显示了数值结果,在图15中显示了生成的重构。通过选择相同的图像作为目标,将结果与 L V A E \mathcal{L}_{VAE} LVAE进行比较也很有趣。对于表3中相同的目标图像, L V A E \mathcal{L}_{VAE} LVAE的结果显示在附录中的表6中。两次攻击的结果是相同的,这是意料之中的,因为目标图像是相同的,只是两种方法的损失函数不同。


5.2 SVHN
SVHN数据集由剪裁过的街道编号图像组成,远不如MNIST清晰。由于处理图像的方式,每个图像可能包含一个以上的数字;目标数字大致在中间。VAE-GAN生成高质量的原始图像重建,如图17所示。

对于分类器攻击,我们在测试了一定范围的值后设置 λ = 1 0 − 5 λ = 10^{-5} λ=10−5,尽管我们无法找到针对SVHN的这种攻击的有效值。对于潜在攻击和 L V A E \mathcal{L}_{VAE} LVAE攻击,我们设 λ = 10 λ = 10 λ=10。

在表10中,我们展示了用于 L 2 L_2 L2优化潜在攻击的 A S i g n o r e − t a r g e t AS_{ignore-target} ASignore−target和 A S t a r g e t AS_{target} AStarget。SVHN上的评估指标不如MNIST上的强,但攻击者仍然可以直接找到几乎所有源/目标对的成功攻击。图2支持这种评估。目视检查显示,12个对抗样本中有11个被重构为目标数字0。值得注意的是,12个对抗样本中有2个看起来像0(第1行和第11行),另外两个既像原始数字又像0,取决于查看者关注的是图像的亮区还是暗区(第4行和第7行)。在SVHN上, L 2 L_2 L2优化潜在攻击比 L V A E \mathcal{L}_{VAE} LVAE攻击获得更好的结果(见表11和图6),而这两种攻击在MNIST上同样有效。


5.3 CELEBA
CelebA的数据集包含20多万张经过裁剪的名人脸,每张脸都有40种不同属性的注释。在我们的实验中,我们进一步将图像缩放到 64 × 64 64 \times 64 64×64,并忽略属性注释。原始图像经过训练后的VAE-GAN重建如图19所示。

由于人脸没有自然分类,我们只评估潜在空间和 L V A E \mathcal{L}_{VAE} LVAE攻击。对于两种攻击,我们都尝试了从 0.1 0.1 0.1到 0.75 0.75 0.75的lambdas。图20显示了使用潜在攻击和lambda值 0.5 0.5 0.5(原始图像和生成的对抗样本之间的 L 2 L_2 L2范数 9.78 9.78 9.78,RMSD 0.088 0.088 0.088)以及相应的VAE-GAN重建生成的对抗样本。大多数重建都能很好地反映目标图像。使用lambda值 0.75 0.75 0.75(原始图像和生成的对抗样本之间的 L 2 L_2 L2范数 8.98 8.98 8.98,RMSD 0.081 0.081 0.081),我们在 L V A E \mathcal{L}_{VAE} LVAE攻击中获得了更好的结果,如图21所示。


5.4 不同攻击方法的总结
表1显示了三种不同攻击方法的原始图像和生成的对抗样本之间的平均距离的比较。原始图像与敌对扰动之间的距离越大,扰动就越明显,人类观察者就越有可能不再识别原始输入,因此有效的攻击在保持这些距离小的同时仍能达到目标。在我们的实验中,潜在攻击的结果始终是最好的,分类器攻击的结果是最差的。

我们还测量使用给定的攻击方法生成 1000 1000 1000个对抗样本所需的时间。到目前为止, L V A E \mathcal{L}_{VAE} LVAE攻击是三种攻击中最慢的,因为它需要在生成对抗样本时,在优化器的每一步都计算完整的重构。另外两种攻击在优化对抗样本时不需要运行重构步骤。
6 结论
我们探索了生成对抗样本,以对抗生成模型,如VAEs和VAE-GANs。这些模型也容易受到对抗的攻击,因为对抗样本会说服它们将输入转换为不同的输出。我们还探究了为什么攻击者可能想要攻击生成模型。鉴于我们成功地将对抗攻击应用于流行的生成模型,我们的工作进一步支持了对抗样本是当前神经网络结构的普遍现象的假设。在这项工作中,我们正在帮助为理解如何建立更强健的网络奠定基础。未来的工作将深入探讨防御和鲁棒性,以及使用自然图像数据集(如CIFAR-10和ImageNet)训练的生成模型的攻击。
Kos J, Fischer I, Song D. Adversarial examples for generative models[C]//2018 ieee security and privacy workshops (spw). IEEE, 2018: 36-42.