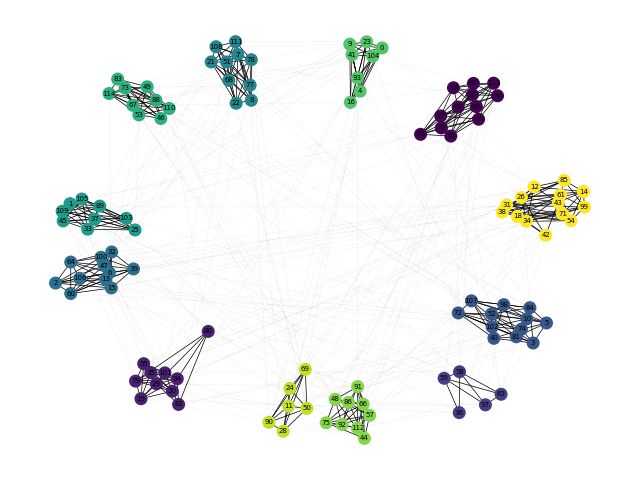
社区发现算法——(Spectral Clustering)谱聚类算法
归一化的拉普拉斯(The unnormalized graph Laplacian):
L = D − W L = D - W L=D−W
其中D为对角度矩阵,W为权重邻接矩阵。
1.矩阵L满足以下性质:
- 对于任一向量 f ∈ R n f \in \mathbb{R}^n f∈Rn, 有 f ′ L f = 1 2 ∑ i , j = 1 n w i j ( f i − f j ) 2 f'Lf = \frac{1}{2}\sum\limits_{i,j=1}^n w_{ij}(f_i - f_j)^2 f′Lf=21i,j=1∑nwij(fi−fj)2.
- L是对称半正定的.
- L最小的特征值为0,对应的特征向量为常数向量 1 \mathbb{1} 1.
- L有n个非负的实值特征值 0 = λ 1 ≤ λ 2 ≤ . . . ≤ λ n 0=\lambda_1\le\lambda_2\le...\le\lambda_n 0=λ1≤λ2≤...≤λn.
需要注意的是非归一化的拉普拉斯算子不依赖于邻接矩阵W的对角元素,所有在非对角线位置上和W重叠的邻接矩阵都会有相同的归一化图拉普拉斯L,图中的环不会改变L。
2.连通分支数量和L的谱:
设G是一个权重非负的无向图,L的0特征值的重数等于图中连通分支的数量。特征值0组成的特征空间由这些分量的指示向量 1 \mathbb{1} 1跨度。
归一化拉普拉斯(The normalized graph Laplacians):
有两种举证被称为归一化图拉普拉斯矩阵,两个矩阵都是密切相关的。
L s y m : = D − 1 2 L D − 1 2 = I − D − 1 2 W D − 1 2 L r w : = D − 1 L = I − D − 1 W L_{sym}:=D^{-\frac{1}{2}}LD^{-\frac{1}{2}} = I - D^{-\frac{1}{2}}WD^{-\frac{1}{2}}\\ L_{rw}:=D^{-1}L = I-D^{-1}W Lsym:=D−21LD−21=I−D−21WD−21Lrw:=D−1L=I−D−1W
其中第一个矩阵是对称矩阵,第二个与随机游走密切相关。
归一化拉普拉斯算子满足以下性质:
- 对于任一向量 f ∈ R n f \in \mathbb{R}^n f∈Rn, 有 f ′ L s y m f = 1 2 ∑ i , j = 1 n w i j ( f i d i − f j d j ) 2 f'L_{sym}f = \frac{1}{2}\sum\limits_{i,j=1}^n w_{ij}(\frac{f_i}{\sqrt{d_i}} - \frac{f_j}{\sqrt{d_j}})^2 f′Lsymf=21i,j=1∑nwij(difi−djfj)2.
- λ \lambda λ是具有特征向量u的 L r w L_{rw} Lrw特征值当且仅当 λ \lambda λ是具有特征向量 w = D 1 2 u w = D^{\frac{1}{2}}u w=D21u的 L s y m L_{sym} Lsym的特征值.
- λ \lambda λ是具有特征向量u的 L r w L_{rw} Lrw特征值当且仅当 λ \lambda λ和u解决了广义特征问题 L u = λ D u Lu = \lambda Du Lu=λDu.
- 0是 L r w L_{rw} Lrw的特征值,特征向量为常数向量 1 \mathbb{1} 1. 0是 L s y m L_{sym} Lsym的特征值,特征向量为 D 1 2 1 D^\frac{1}{2} \mathbb{1} D211.
- L s y m , L r w L_{sym},L_{rw} Lsym,Lrw是半正定的,具有n个非负特征值 0 = λ 1 ≤ λ 2 ≤ . . . ≤ λ n 0=\lambda_1\le\lambda_2\le...\le\lambda_n 0=λ1≤λ2≤...≤λn.
连通分支数量和L的谱:
设G是一个权重非负的无向图,L的0特征值的重数等于图中连通分支的数量。
谱聚类算法:
通过一些相速度函数度量除相似度矩阵S,该矩阵为对称非负的。
非归一化谱聚类算法:
- 输入:相似度矩阵,聚类类别数目k.
- 计算非归一化拉普拉斯L
- 计算L最小的k个特征值对应的特征向量
- 设U是以这些特征向量作为每一列组成的矩阵
- 对于i=1…,n,设 y i ∈ R k y_i \in \mathbb{R}^k yi∈Rk是U第i行对应的向量
- 使用k-means算法将所有 y i y_i yi聚类为k个社区 C 1 , . . . , C k C_1,...,C_k C1,...,Ck.
- 输出:社区 A 1 , . . . , A k w i t h A i = { j ∣ y j ∈ C i } A_1,...,A_k \;with\;A_i = \{j|y_j\in C_i\} A1,...,AkwithAi={j∣yj∈Ci}.
归一化谱聚类算法 L r w L_{rw} Lrw:
-
输入:相似度矩阵,聚类类别数目k.
-
计算归一化拉普拉斯L
-
计算广义特征问题 L u = λ D u Lu = \lambda Du Lu=λDu最小的K个广义特征向量
-
设U是以这些特征向量作为每一列组成的矩阵
-
对于i=1…,n,设 y i ∈ R k y_i \in \mathbb{R}^k yi∈Rk是U第i行对应的向量
-
使用k-means算法将所有 y i y_i yi聚类为k个社区 C 1 , . . . , C k C_1,...,C_k C1,...,Ck.
-
输出:社区 A 1 , . . . , A k w i t h A i = { j ∣ y j ∈ C i } A_1,...,A_k \;with\;A_i = \{j|y_j\in C_i\} A1,...,AkwithAi={j∣yj∈Ci}.
注意,该算法使用了L的广义特征向量,它对应于矩阵Lrw的特征向量。
归一化谱聚类算法 L s y m L_{sym} Lsym:
- 输入:相似度矩阵,聚类类别数目k.
- 计算归一化拉普拉斯 L s y m L_{sym} Lsym
- 计算 L s y m L_{sym} Lsym 最小的k个特征值对应的特征向量
- 设U是以这些特征向量作为每一列组成的矩阵
- 将U进行归一化每行化为范数1,形成矩阵 T ∈ R n × k T \in \mathbb{R}^{n \times k} T∈Rn×k,设置 t i j = u i j ( ∑ k u i k 2 ) 1 / 2 t_{ij} = \frac{u_{ij}}{(\sum_k u_{ik}^2)^{1/2}} tij=(∑kuik2)1/2uij.
- 对于i=1…,n,设 y i ∈ R k y_i \in \mathbb{R}^k yi∈Rk是T第i行对应的向量
- 使用k-means算法将所有 y i y_i yi聚类为k个社区 C 1 , . . . , C k C_1,...,C_k C1,...,Ck.
- 输出:社区 A 1 , . . . , A k w i t h A i = { j ∣ y j ∈ C i } A_1,...,A_k \;with\;A_i = \{j|y_j\in C_i\} A1,...,AkwithAi={j∣yj∈Ci}.
除了它们使用了三种不同的拉普拉斯图外,上述三种算法看起来非常相似。它们的主要技巧是将抽象数据点x的表示改为y。正是由于拉普拉斯图的性质,这种表示的改变是有用的。这种表示方式的改变增强了数据中的集群属性,因此在新的表示方式中可以很容易地检测到集群。
我们可以从切图、随机游走、Perturbation theory的观点推导出谱聚类。
切图观点:
从切图的观点推导出谱聚类。
谱聚类(spectral clustering)及其实现详解_杨铖的博客-CSDN博客_谱聚类实现
我们想找到一种划分,使得不同社区之间的变得权重低,社区内的权重高。
可以通过最小化下式实现:
意思是图中社区到其他社区的权重总和,前面的1/2防止每条边计算两次。但上式在实践中效果并不好,很多情况它的解只是简单的从图的其他部分分离出一个单独的顶点,这显然不是我们想要的,社区中应该是合理的大型点群。所以我们要明确要求每个A集足够大。编码这个的最常见的目标函数是RatioCut以及Ncut。
在RationCut中,图的一个子集A的大小是由它的顶点数目|A|来度量的。而在Ncut中,大小是由他的边的权重和vol(A)度量的。具体定义如下: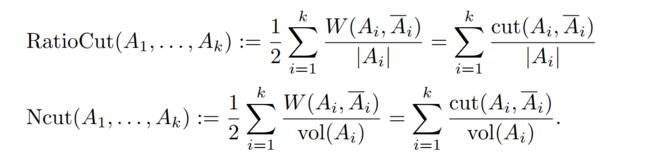





与谱聚类相关的一个基本问题是,应该使用三个图中的哪一个拉普拉斯来计算特征向量。如果图是非常规则的,并且大多数顶点具有近似相同的度,那么所有的拉普拉斯算子都非常相似,并且同样适用于聚类。然而,如果图中的度分布很广,那么拉普拉斯函数就有很大的不同。在我们看来,有几个论点主张使用归一化谱聚类而不是非归一化谱聚类,在归一化的情况下使用Lrw的特征向量而不是Lsym的特征向量。
Python代码实现下载
import networkx as nx
import numpy as np
from sklearn.cluster import KMeans
import scipy.linalg as linalg
from matplotlib import pyplot as plt
def partition(G, k):
# 获得邻接矩阵
A = nx.to_numpy_array(G)
# 获得度矩阵
D = degree_matrix(G)
# 获得拉普拉斯算子
L = D - A
# 获得归一化拉普拉斯算子Lsm
Dn = np.power(np.linalg.matrix_power(D, -1), 0.5)
L = np.dot(np.dot(Dn, L), Dn)
# L = np.dot(Dn, L)
# 获得特征值,特征向量
eigvals, eigvecs = linalg.eig(L)
n = len(eigvals)
dict_eigvals = dict(zip(eigvals, range(0, n)))
# 获得前k个特征值
k_eigvals = np.sort(eigvals)[0:k]
eigval_indexs = [dict_eigvals[k] for k in k_eigvals]
k_eigvecs = eigvecs[:, eigval_indexs]
# 归一化
# sum_co = k_eigvecs.sum(axis=0)
# norm_ans = k_eigvecs/sum_co
# 使用k-means聚类
result = KMeans(n_clusters=k).fit_predict(k_eigvecs)
# result = KMeans(n_clusters=k).fit_predict(norm_ans)
return result
def degree_matrix(G):
n = G.number_of_nodes()
V = [node for node in G.nodes()]
D = np.zeros((n, n))
for i in range(n):
node = V[i]
d_node = G.degree(node)
D[i][i] = d_node
return np.array(D)
if __name__ == '__main__':
G = nx.read_edgelist("data/football.txt")
k = 12
sc_com = partition(G, k)
print(sc_com)
# 可视化
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=False, node_size=70, width=0.5, node_color=sc_com)
plt.show()
V = [node for node in G.nodes()]
com_dict = {node: com for node, com in zip(V, sc_com)}
com = [[V[i] for i in range(G.number_of_nodes()) if sc_com[i] == j] for j in range(k)]
# 构造可视化所需要的图
G_graph = nx.Graph()
for each in com:
G_graph.update(nx.subgraph(G, each)) #
color = [com_dict[node] for node in G_graph.nodes()]
# 可视化
pos = nx.spring_layout(G_graph, seed=4, k=0.33)
nx.draw(G, pos, with_labels=False, node_size=1, width=0.1, alpha=0.2)
nx.draw(G_graph, pos, with_labels=True, node_color=color, node_size=70, width=0.5, font_size=5,
font_color='#000000')
plt.show()