社区发现算法——Walktrap算法

论文出处：Computing Communities in Large Networks Using Random Walks

本文有以下贡献:

• 新的基于随机行走的算法称为Walktrap，它计算给定图的社区结构。它在最坏情况下的复杂度是O(mn2)时间和O(n2)空间，而在大多数情况下是O(n2log n)时间和O(n2)空间
• 基于随机游动的顶点之间(和社区之间)相似性的新度量®。 与之前的方法相比，该距离度量方法计算效率高，能够很好地捕捉社区结构的信息。
• 新的度量(η)来评估一个图划分成社区的质量。这个度量能够在不同的尺度上识别相关的分区。
• 大量的比较测试表明，Walktrap在社区结构的质量方面超过了以前的方法，在运行时间方面也是最好的方法之一。
• 论文还提供了大量的证据和与谱方法的关系。

关键概念：

**关键思想是图上的随机游走容易陷入密集连接的子图中，即社区当中。**这表明随机游走可以用来确定顶点之间和社区之间的距离度量。因此，得到的距离可以通过聚类算法计算出用树状图表示的分层的社区结构。

在效率方面，这种方法比谱聚类更好，它避免了昂贵的特征向量显式计算。

随机游走：

图G上的随机游走由它的转移矩阵P驱动，这个P可以从图G的邻接矩阵A中得到。长度t的随机游走可以用矩阵$P^t$表示, 其中$P_{ij}^t=(P^t{)}_{ij}$是第t步中从顶点i到顶点j的概率。参数t的设置应该使随机游走足够长保证能收集到关于图的拓扑结构的足够信息，但也不能太长以免达到平衡分布。

然后我们可以利用概率$P_{ij}^t$确定节点i和j之间的相似度:
$$r_{ij}=||D^{-\frac{1}{2}}{P}_{i.}^t-D^{-\frac{1}{2}}{P}_{j.}^t||$$
$||\cdot ||$是欧几里得范数，$P_{i.}^t$是$P^t$的第i行，D是节点的度对角矩阵。

如果两个顶点属于不同的社区rij距离较大，属于同一社区时小。

同理，我们可以定义不同社区之间的距离：
$$r_{C_1{C}_2}=||D^{-\frac{1}{2}}{P}_{C_1.}^t-D^{-\frac{1}{2}}{P}_{C_2.}^t||$$
其中$P_{C.}^t$是由各元素定义的概率向量：
$$P_{Cj}^t=\frac{1}{|C|}\sum _{i\in C}{P}_{ij}^t$$
定义了在t步中，从社区C到顶点j的概率。

层次聚类:

下一步是使用这些距离来执行层次聚类。在每一步中，我们合并两个相邻的社区C1和C2，使当前划分中所有社区对之间的变化$\Delta \sigma (C_1,C_2)$最小:(算法中的eq3)
$$\Delta \sigma (C_1,C_2)=\frac{1}{n}\frac{|C_1||C_2|}{|C_1|+|C_2|}{r}_{C_1{C}_2}^2\text{\hspace{1em}(3)}$$
这个量决定了当合并C1和C2，每个顶点与其社区之间距离的平方均值的增加。值得注意的是r代表欧氏距离，这一事实使得$\Delta \sigma$的计算非常有效。

在合并C1和C2以后，我们还需要更新C3和所有受影响的社区C之间的$\Delta \sigma (C_3,C)$的值，即以前C1或C2的邻居社区。可以看出，如果C1和C2都和C相邻，则可以利用C有效计算$\Delta \sigma (C_3,C)$：(算法中的eq4)
$$\Delta \sigma (C_3,C)=\frac{(|C_1|+|C|)\Delta \sigma (C_1,C)+(|C_2|+|C|)\Delta \sigma (C_2,C)-|C|\Delta \sigma (C_1,C_2)}{|C_3|+|C|}\text{\hspace{1em}(4)}$$

否则用前面的式子eq3计算就行

划分的质量：

在每个合并步骤K，算法生成一个划分Pk，为了选择最佳的P划分，我们需要定义一个划分的质量指标。最常用的度量是模块度Q：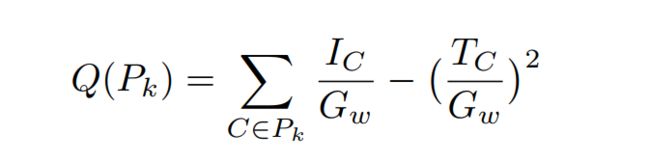
其中，Ic和Tc分别是社区C的内部权重值和总的权重值，Gw是图的总权重，这里不考虑环。选择Q最大的划分作为最好划分情况。

适合寻找唯一的划分情况，但不适合寻找不同尺度的社区。

为了解决模量性的这一局限性，本文提出了一个新的质量判据η，其定义为:

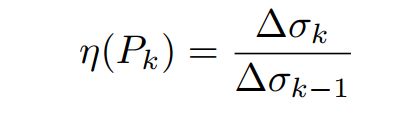
其中，∆σk是最小∆σ，它决定了在迭代k时合并哪些群落。然后根据$P\ast =argma{x}_{Pk-1}\eta (P_k)$选择最佳分区P∗。这里的直觉是，如果我们合并两个非常不同的群落(在距离r方面)，那么这一步的∆σk值很大，这表明在第k - 1步的社区结构是合适的。

优点:可以揭示不同尺度的相关群落结构。 缺点:可能需要另一个标准(例如社区大小)来选择确定的最佳分区。

与真实划分比较：

校正兰德系数:

限制：

无法处理有向图

无法处理非常大的图形(数百万个顶点)，因为它对内存的要求很高。

只生成不重叠的社区，不能用于重叠社区发现。

算法伪代码：

python代码：下载

import numpy as np
import networkx as nx
from heapq import heappush, heappop
from matplotlib import pyplot as plt
import copy
import time


def walktrap(G, t, verbose=False):
    class Community:
        def __init__(self, new_C_id, C1=None, C2=None):
            self.id = new_C_id
            # 一个节点作为一个社区
            if C1 is None:
                self.size = 1
                self.P_c = P_t[self.id]  # probab vector
                self.adj_coms = {}
                self.vertices = set([self.id])
                self.internal_weight = 0.
                self.total_weight = self.internal_weight + (len([id for id, x in enumerate(A[self.id]) if
                                                                 x == 1. and id != self.id]) / 2.)  # External edges have 0.5 weight, ignore edge to itself
            # 合并形成新社区
            else:
                self.size = C1.size + C2.size
                self.P_c = (C1.size * C1.P_c + C2.size * C2.P_c) / self.size
                # Merge info about adjacent communities, but remove C1, C2
                self.adj_coms = dict(C1.adj_coms.items() | C2.adj_coms.items())
                del self.adj_coms[C1.id]
                del self.adj_coms[C2.id]
                self.vertices = C1.vertices.union(C2.vertices)
                weight_between_C1C2 = 0.
                for v1 in C1.vertices:
                    for id, x in enumerate(A[v1]):
                        if x == 1. and id in C2.vertices:
                            weight_between_C1C2 += 1.
                self.internal_weight = C1.internal_weight + C2.internal_weight + weight_between_C1C2
                self.total_weight = C1.total_weight + C2.total_weight

        def modularity(self):
            # 模块度计算
            return (self.internal_weight - (self.total_weight * self.total_weight / G_total_weight)) / G_total_weight

    # 获得节点数目
    N = G.number_of_nodes()
    # 获得邻接矩阵
    A = np.array(nx.to_numpy_matrix(G))

    # 转移矩阵P 以及 对角度矩阵D
    Dx = np.zeros((N, N))
    P = np.zeros((N, N))
    # 遍历邻接矩阵的每一行 对应每个节点与其他节点的邻接关系
    for i, A_row in enumerate(A):
        # 邻接矩阵一行的和为对应节点的度
        d_i = np.sum(A_row)
        # 转移概率 等于每个邻居节点的权重除以该节点的度
        P[i] = A_row / d_i
        # 后面计算都是D-0.5 提前处理好方便后面计算
        Dx[i, i] = d_i ** (-0.5)

    # 采用t次随机游走
    P_t = np.linalg.matrix_power(P, t)

    # 边的总权重
    G_total_weight = G.number_of_edges()

    # 当前的社区
    community_count = N
    communities = {}
    # 刚开始将每个节点作为一个社区
    for C_id in range(N):
        communities[C_id] = Community(C_id)

    # 储存Δσ: 
    min_sigma_heap = []
    # 遍历所有相邻节点 计算Δσ
    for e in G.edges:
        C1_id = e[0]
        C2_id = e[1]
        if C1_id != C2_id:
            # 利用公式计算 这里|c1||c2|\(|c1|+|c2|)个数都是1直接等于0.5
            ds = (0.5 / N) * np.sum(np.square(np.matmul(Dx, P_t[C1_id]) - np.matmul(Dx, P_t[C2_id])))
            # 利用堆排序存储
            heappush(min_sigma_heap, (ds, C1_id, C2_id))
            # 更新每个社区以及它的邻居社区
            communities[C1_id].adj_coms[C2_id] = ds
            communities[C2_id].adj_coms[C1_id] = ds

    delta_sigmas = []

    partitions = [set(np.arange(N))]
    # 第一次划分时每个节点为自身的社区
    # 计算初始模块度Q
    modularities = [np.sum([communities[C_id].modularity() for C_id in partitions[0]])]
    if verbose:
        print("Partition 0: ", partitions[0])
        print("Q(0) = ", modularities[0])

    # 开始迭代
    for k in range(1, N):
        # 根据最小的Δσ合并C1,C2
        # 需要确保最小的Δσ的C1,C2仍然在当前的划分社区列表中
        while min_sigma_heap:
            # 取出当前最小的Δσ
            delta_sigma_C1C2, C1_id, C2_id = heappop(min_sigma_heap)
            if C1_id in partitions[k - 1] and C2_id in partitions[k - 1]:
                break
        # Record delta sigma at this step
        delta_sigmas.append(delta_sigma_C1C2)

        # 合并C1,C2为C3, 分配id
        C3_id = community_count
        community_count += 1  # increase for the next one
        communities[C3_id] = Community(C3_id, communities[C1_id], communities[C2_id])

        # 添加新的划分(k-th)
        partitions.append(copy.deepcopy(partitions[k - 1]))
        partitions[k].add(C3_id)  # add C3_ID
        partitions[k].remove(C1_id)
        partitions[k].remove(C2_id)

        # 更新C3和以前C1或C2的邻居社区之间的delta_sigma_heap
        # 遍历C3的邻居社区
        for C_id in communities[C3_id].adj_coms.keys():
            # 如果C是C1,C2共同的邻居则用公式4
            if (C_id in communities[C1_id].adj_coms) and (C_id in communities[C2_id].adj_coms):
                delta_sigma_C1C = communities[C1_id].adj_coms[C_id]
                delta_sigma_C2C = communities[C2_id].adj_coms[C_id]
                # 使用公式4 to (C, C3)
                ds = ((communities[C1_id].size + communities[C_id].size) * delta_sigma_C1C + (
                        communities[C2_id].size + communities[C_id].size) * delta_sigma_C2C - communities[
                          C_id].size * delta_sigma_C1C2) / (communities[C3_id].size + communities[C_id].size)

            # 否则使用公式3 to (C, C3)
            else:
                ds = np.sum(np.square(np.matmul(Dx, communities[C_id].P_c) - np.matmul(Dx, communities[C3_id].P_c))) * \
                     communities[C_id].size * communities[C3_id].size / (
                             (communities[C_id].size + communities[C3_id].size) * N)

            # 更新min_sigma_heap以及更新C3,C之间的delta sigmas
            heappush(min_sigma_heap, (ds, C3_id, C_id))
            communities[C3_id].adj_coms[C_id] = ds
            communities[C_id].adj_coms[C3_id] = ds

            # 计算并存储当前划分的模块度
        modularities.append(np.sum([communities[C_id].modularity() for C_id in partitions[k]]))

        if verbose:
            print("Partition ", k, ": ", partitions[k])
            print("\tMerging ", C1_id, " + ", C2_id, " --> ", C3_id)
            print("\tQ(", k, ") = ", modularities[k])
            print("\tdelta_sigma = ", delta_sigmas[k - 1])

    return np.array(partitions), communities, np.array(delta_sigmas), np.array(modularities)


# 计算 Rand index
def calculate_rand_index(P1, P2):
    N = 0
    sum_intersect = 0.
    sum_C1 = 0.
    sum_C2 = np.sum([len(s) ** 2 for s in P2])
    for s1 in P1:
        N += len(s1)
        sum_C1 += len(s1) ** 2
        for s2 in P2:
            sum_intersect += len(s1.intersection(s2)) ** 2
    return (N * N * sum_intersect - sum_C1 * sum_C2) / (0.5 * N * N * (sum_C1 + sum_C2) - sum_C1 * sum_C2)


def partition_to_plot(coms, partition):
    p_dict = {}
    for i, C_id in enumerate(partition):
        for v in coms[C_id].vertices:
            p_dict[v] = i
    return p_dict


def partition_dict_to_sets(d):
    inverse_dict = {}
    for k, v in d.items():
        if v in inverse_dict:
            inverse_dict[v].add(k)
        else:
            inverse_dict[v] = set([k])

    return inverse_dict.values()


def partition_set_to_sets(comms, partition):
    list_of_sets = []
    for C_id in partition:
        list_of_sets.append(copy.deepcopy(comms[C_id].vertices))
    return list_of_sets


if __name__ == '__main__':
    G = nx.read_edgelist("data/football.txt")
    k = 12
    G = nx.convert_node_labels_to_integers(G)
    pos = nx.spring_layout(G)

    t = 2
    parts, coms, _, Qs = walktrap(G, t)
    Qmax_index = np.argmax(Qs)
    my_best_part = partition_to_plot(coms, parts[Qmax_index])
    sort_p = sorted(my_best_part.items(), key=lambda x: x[0])
    # print([x[1] for x in sort_p])
    nx.draw(G, pos, node_color=[x[1] for x in sort_p])
    plt.show()
    print(my_best_part)

    print(partition_dict_to_sets(my_best_part))
    print(calculate_rand_index(partition_dict_to_sets(my_best_part), partition_dict_to_sets(my_best_part)))