动态规划&数位DP

这篇博客通过一道经典的题目来学习数位DP。

1. 题目描述

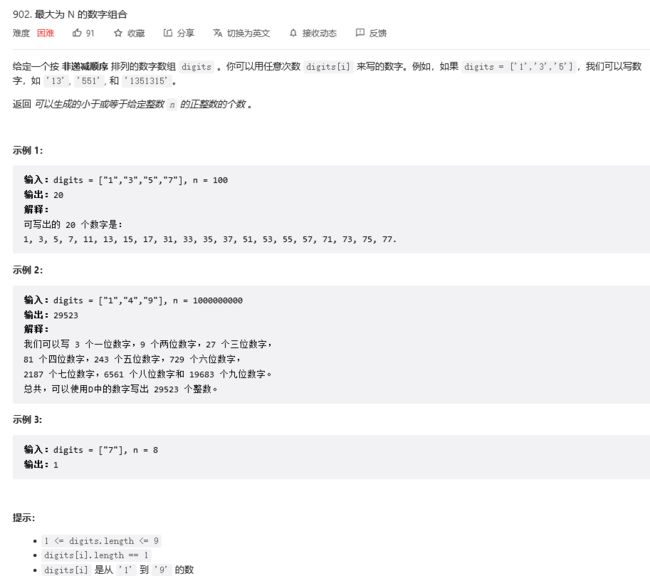
题目链接：902. 最大为 N 的数字组合

2. 思路分析

方法一：

由于题目给定的 digits 不包含 0，因此相当于只需要回答使用 digits 的数值能够覆盖 [1,x]范围内的多少个数字。

先将字符串数组 digits 转为数字数组 nums，假定 nums 的长度为 m，然后考虑如何求得 [1,x] 范围内合法数字的个数。

存在函数int dp (int[] nums, int n),能够返回区间 [1,x] 内合法数的个数，那么配合「容斥原理」我们便能够回答任意区间合法数的查询：res(l, r) = dp(r) - dp(l -1)

对于本题，查询区间的左端点固定为 1，同时 dp(0)=0，因此答案为 dp(n)。

将组成 [1,x] 的合法数分成三类：

• 位数和x相同，且最高位比x最高位要小的，统计为res1
• 位数和x相同，且最高位与x最高位相同的，统计为res2
• 位数比x少，统计为res3

其中 res1 和 res3 求解相对简单，重点落在如何求解 res2 上。

对n进行从高到低的处理，对于第k位而言（不是最高位），假设在n中第k位为cur,只能在[1, cur-1]范围内取数，为了满足数字只能取自 nums」的限制，因此我们可以利用 nums 本身有序，对其进行二分，找到满足 nums[mid] <= cur 的最大下标 right，根据 nums[right] 与 cur 的关系进行分情况讨论：

• nums[right]=cur： k共有right种选择，每个位置有m种选择，共有len-p个位置，由于nums[right] = right，往后的方案还要决策，需要继续处理
• nums[right] < cur：算上nums[right], k共有right +1种选择，每个位置有m种选择，共有len-p个位置，由于nums[right] < right，往后的方案数已经在这次被统计完，累加后break
• nums[right] > cur：该分支往后不再满足，合法方案为0

Java代码实现：

class Solution {
    public int atMostNGivenDigitSet(String[] digits, int n) {
        // 数组DP+二分
        int length = digits.length;
        int[] nums = new int[n];
        for (int i = 0; i < length; i++) {
            nums[i] = Integer.parseInt(digits[i]);
        }
        return dp(nums, n);
    }
    private int dp(int[] nums, int n) {
        List<Integer> list = new ArrayList<>();
        while (n != 0) {  // 将n的各位数加入到list
            list.add(n % 10);
            n /= 10;
        }
        int len = list.size(), m = nums.length, res = 0;
        // 位数和 n 相同
        for (int i = len - 1, p = 1; i >= 0; i--, p++) {
            int cur = list.get(i);
            int left = 0, right = m - 1;
            while (left < right) {  // 二分找到满足nums[mid] <= cur的最大下标
                int mid = left + (right - left) / 2;
                if (nums[mid] <= cur) {
                    left = mid;
                } else {
                    right = mid - 1;
                }
            }
            if (nums[right] > cur) { // 该分支往后不再满足，合法方案为0
                break; 
            } else if (nums[right] == cur) { // k共有right种选择，每个位置有m种选择，共有len-p个位置
                res += right * (int) Math.pow(m, (len - p));
                if (i == 0) res++;  // 由于nums[right] = right，往后的方案还要决策，需要继续处理
            } else if (nums[right] < cur) { // 算上nums[right], k共有right + 1种选择，每个位置有m种选择，共有len-p个位置
                res += (right + 1) * (int) Math.pow(m, (len - p));
                break; // 由于nums[right] < right，往后的方案数已经在这次被统计完，累加后break
            }
        }
        // 位数比n少的
        for (int i = 1, last = 1; i < len; i++) {
            int cur = last * m;
            res += cur;
            last = cur;
        }
        return res;
    }
}

方法二：

设 n 是一个 K 位数，那么对于任意一个位数小于 K（假设有 k 位，即 k < K）的数，如果它仅包含 digits 中出现的数字，那么它就是合法的，并且 k 位数中，合法的数一共有 |D|^k 个

考虑完位数小于 K 的数，我们接下来考虑位数等于 K 的数，我们用 N = 2345 作为例子来考虑所有合法的 K = 4 位数。

• 如果第 1 个数位比 n 中对应的第 1 个数位（即 2）小，那么剩下的 3 个数位我们可以使用 D 中的任何一个数字，因此有 D^k-1 个合法的数。
• 如果第 1 个数位和 n 中对应的第 1 个数位（即 2）相等，那么从第 2 个数位开始，它既可以比 n 中对应的第 2 个数位（即 3）小，也可以相等。此时相当于我们在考虑一个 K - 1 位数的问题。

我们用 dp[i] 表示小于等于 n 中最后 n - i 位数的合法数的个数，例如当 n = 2345 时，dp[0], dp[1], dp[2], dp[3] 分别表示小于等于 2345, 345, 45, 5 的合法数的个数。我们从大到小计算 dp[i]，状态转移方程为：dp[i] = (number of d in D with d < S[i]) * ((D) ** (n - i - 1))

即我们枚举第 n - i 位数，后面的 n - i - 1 位数可以在 D 中任选。如果 N 的第 n - i 位数在 D 中，上述的状态转移方程还需要加上一项 dp[i + 1]。

最终的答案为 dp[0] 加上所有 k < K 位的合法的数。

Java代码实现：

class Solution {
    public int atMostNGivenDigitSet(String[] digits, int n) {
        // dp[i] 表示小于等于n中最后n-i位数的合法数的个数
        String str = String.valueOf(n);
        int len = str.length();
        int[] dp = new int[len + 1];
        dp[len] = 1; //初始化
        for (int i = len - 1; i >=0; i--) {
            int num = str.charAt(i) - '0';
            for (String s : digits) {
                if (Integer.valueOf(s) < num) {
                    dp[i] += Math.pow(digits.length, len - i - 1);
                } else if (Integer.valueOf(s) == num) {
                    dp[i] += dp[i + 1];
                } else {
                    break;
                }
            }
        }
        for (int i = 1; i < len; i++) {
            dp[0] += Math.pow(digits.length, i);
        }
        return dp[0];
    }
}

参考：

【动态规划の数位 DP】一文详解通用「数位 DP」求解思路

官方题解：最大为 N 的数字组合