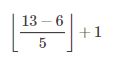yolov3--16--一文详解卷积操作中的padding填充操作

Yolov-1-TX2上用YOLOv3训练自己数据集的流程(VOC2007-TX2-GPU)

Yolov--2--一文全面了解深度学习性能优化加速引擎---TensorRT

Yolov--3--TensorRT中yolov3性能优化加速（基于caffe）

yolov-5-目标检测：YOLOv2算法原理详解

yolov--8--Tensorflow实现YOLO v3

yolov--9--YOLO v3的剪枝优化

yolov--10--目标检测模型的参数评估指标详解、概念解析

yolov--11--YOLO v3的原版训练记录、mAP、AP、recall、precision、time等评价指标计算

yolov--12--YOLOv3的原理深度剖析和关键点讲解

---

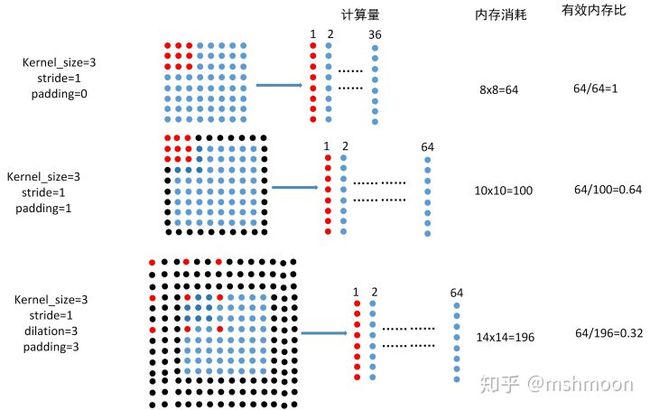
如上图所示:

第一行为普通3x3卷积，步长1，padding 0,

第二行为普通3x3卷积，步长1，padding 1,

第三行为膨胀3x3卷积,dilation rate=3，步长1，padding 3.

上图箭头右向所指，为cnn底层在caffe 和darknet的底层实现，用c或c++，至于pytorch和tensorflow 是否也是这样实现cnn我不清楚，但是目前来讲，有效实现卷积的也就3种方式，

im2col(上图) ，winograd, FFT，但是还是im2col比较常见，winograd好像是商汤最近几年提出来的，通过特殊数学计算方式，减少计算量，目前该方法被应用在腾讯移动端深度学习框架NCNN中，至于FFT，还没见到用在深度学习种。

至于为什么使用im2col,这还是贾清扬大神在写caffe时提出来的，因为图像中，一个块内的像素点在内存中是地址不连续的，所以对于同一个块内的像素想要缓存到cache上，可能出现多次内存访问，效率极低，所以设计出im2co方式，提前将需要计算的像素点放在连续地址上。

因此，对于同一图像，除了原始图像在内存中占空间，使用im2col又会消耗另一份空间。

如上图所示,对于8x8的图像:

不加padding,计算量为9x36=324, 内存消耗为8x8=64,有效内存为64/64=1

加padding=1,计算量为9x64=572,内存消耗为10x10=100,有效内存为64/100=0.64

加dilation_rate=3,padding=1,计算量为9x64=572,内存消耗为14x14=196，有效内存为64/196=0.32

在上图中可见，

添加padding=1就可对内存造成1-0.64=0.36的内存损失，当使用dilation_rate=3时，内存损失为1-0.32=0.68

假如，我们为存储图像分配1个G大小空间，为使用im2col后的图像在分配1个G大小的空间，当我们使用dilation_rate=3之后，有效内存，也就是真正的像素所占的内存仅仅为2x0.32=0.64G。

以上例子为当图像或是特征大小为8x8的情况，假设我们的图像或是特征大小为100x100

那么使用dilation_rate=3，有效内存占比为（100x100）/(106x106)=0.88，有效内存还是挺客观的。

对于8x8的如此小的特征，在我们的网络中一般都出现在网络的深层，而对于100x100的特征，在我们的网络中一般都出现在网络的浅层。因此在网络不同的层中，合理使用dilation，

可以更高效的使用我们的内存。

---

在valid情况下，  输出形状计算方法为： new_height=new_width=[(W-F)/S+1]

在same情况下，输出形状计算方法为： new_height=new_width=[W/S]

其中W为输入的尺寸，F为滤波器尺寸，S为步长，[ ]为向上取整函数。

由上可知，如果要保持卷积或池化之后的图像尺寸不变，则步长S必须为1。

---

卷积padding的补0策略

作为最基础的卷积层——CNN，我们应当对他最为熟悉。但是在实现的时候，忽然发现对于其第一步骤，就有困惑的地方，那就是padding，也就是补0策略。

在Keras中，卷积层的定义是如下：

keras.layers.convolutional.Conv1D(filters, kernel_size, strides=1, padding='valid', dilation_rate=1, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)

可以看到padding是一个参数，它有可选值，根据官方文档说明，它总共包含3种可选值：’valid’,’same’和‘casual’.那么这每个意思也进行了描述，但是具体如何操作呢？

“valid”代表只进行有效的卷积，即对边界数据不处理。这个是非常容易理解的，即不进行补0，能有多少卷积就有多少卷积，但是会抛弃一些数据，而且每次总是最后的数字被抛弃。这也可能造成右边界数据没有顾忌到的缺陷。

例如，一个序列有13长，我们的kernel_size为6，步长为5，那么采用valid的补0策略的卷积后的大小为2，即 

“same”代表进行补0卷积，但是它的补0也是有上限的，它的第一步卷积补0为kernel_size-strides，然后到最后剩多少补多少0，如果采用same补0策略的卷积，那么上面例子中的卷积后大小为3，即 

“casual”则是代表具有时序关系的卷积，即output[t]不依赖于input[t+1：]。当对不能违反时间顺序的时序信号建模时有用。一般不使用这种。

总结：如果卷积的方式选择为same,那么卷积操作的输入和输出尺寸会保持一致。如果选择valid,那卷积过后,尺寸会变小。

一个例子

比如输入图片是28*28的单通道图片，其输入shape为[batch_size, 28, 28, 1]; 

• 第一层卷积为32个5*5卷积核，其shape为[5,5,1,32]，其步长strides为[1,1,1,1]，紧接着是第一层的2*2的max_pooling，其形状为[1,2,2,1]，其步长strides为[1,2,2,1]; 

• 第二层卷积为64个5*5卷积核，其shape为[5,5,32,64]，其步长strides为[1,1,1,1]，紧接着是第一层的2*2的max_pooling，其形状为[1,2,2,1]，其步长strides为[1,2,2,1]; 

• padding全部使用SAME; 

那么图像的尺寸经过以上两次卷积，两次池化后的变化如下： 
[batch_size, 28, 28, 1] 
↓ (第一层卷积)
[batch_size, 28, 28, 32] 
↓ (第一层池化)
[batch_size, 14, 14, 32] 
↓ (第二层卷积)
[batch_size, 14, 14, 64] 
↓ (第二层池化)
[batch_size, 7, 7, 64] 

如果上述所有的卷积核，池化核以及步长都保持不变，但是全部使用VALID模式，那么尺寸变化如下：
[batch_size, 28, 28, 1] 
↓ (第一层卷积)
[batch_size, 24, 24, 32] 
↓ (第一层池化)
[batch_size, 12, 12, 32] 
↓ (第二层卷积)
[batch_size, 8, 8, 64] 
↓ (第二层池化)
[batch_size, 4, 4, 64] 

---

例子：

W = tf.truncated_normal([5, 5, 1, 32], stddev=0.1)
tf.nn.conv2d(x, W, strides=[1, 2, 2, 1], padding='SAME')

1、shape= [5,5,1,32]

前面两个5,表示卷积核的长宽分别为5

1表示输入图像对应的通道数，比如输入的图像是单通道的则设置为1，如果是RGB三通道的，则设置为3

32表示卷积核的个数，对应输出32张图

2、strides=[1, 2, 2, 1]

四个元素规定前后必须为1，中间两个数表示水平滑动和垂直滑动步长值

3、padding='SAME'SAME表示在扫描的时候，如果遇到卷积核比剩下的元素要大时，这个时候需要补0进行最后一次的行扫描或者列扫描

在卷积核移动逐渐扫描整体图时候，因为步长的设置问题，可能导致剩下未扫描的空间不足以提供给卷积核的

4、比如有图大小为5*5,卷积核为2*2,步长为2,卷积核扫描了两次后，剩下一个元素，不够卷积核扫描了，这个时候就在后面补零，补完后满足卷积核的扫描，这种方式就是same。如果说把刚才不足以扫描的元素位置抛弃掉，就是valid方式。

---

若加微信请备注下姓名_公司/学校，相遇即缘分，感谢您的支持，愿真诚交流，共同进步，谢谢~ 

 

 

---

https://blog.csdn.net/oMoDao1/article/details/84994437

https://zhuanlan.zhihu.com/p/66289618

https://blog.csdn.net/qq_35082030/article/details/80079563

https://blog.csdn.net/u011304078/article/details/83537514