昨天,我用 Python 写了一个婚介模型
![]()
![]()
作者 | 天元浪子
来源 | CSDN(ID:CSDNnews)
先声明一下:本文纯属七夕应景娱乐之作。如果有人因为遵循本模型提出的择偶理论而导致失恋或单身,除了同情,我不能补偿更多。
在中国的传统节日里,七夕可能是起源最神秘、内涵最深刻的一个了。当然,这不是本文的重点,我们的核心问题是:在七夕这个特有纪念意义的日子,你真的想好了要向TA表白吗?TA 真的是你唯一正确的选择吗?这个婚介模型,也许对你有一些启发。
我的婚介所生意兴隆,无数想找到理想伴侣的单身人士都来光顾。根据颜值、人品、能力、财富等因素,我给每位客户确定了一个素质指数(Quality Index),简写为 qidx。统计发现,qidx 呈现均值 8.0、标准差 0.5 正态分布。
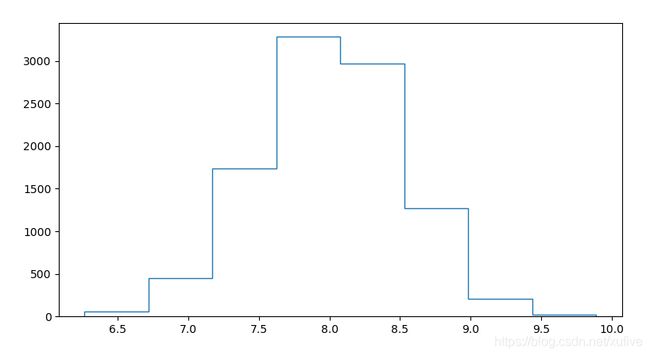
下面是1万客户的 qidx 统计分布图,可以看出绝大多数单身人士的 qidx 位于 7.0~9.0 之间,评价较为负面的和非常优秀的,都属于少数派。
import numpy as np
import matplotlib.pyplot as plt
singles = np.random.normal(loc=8.0, scale=0.5, size=10000)
plt.hist(singles, bins=8, histtype='step')
plt.show()
一般情况下,我的客户缴费 1 次,将获得有 10 次选择机会。我向客户推荐目标的策略基于“门当户对”,总是选择和客户的 qidx 相适应的异性,具体说就是以客户的 qidx 为均值,以 0.1 的方差,按照正态分布随机生成。
通常,客户有两种方式从我为他们推荐的目标中做出选择。第一种是基于传统的择偶观念,具体规则如下:
有 10% 的客户会对当前的推荐目标一见钟情,不在意双方的 qid 是否匹配。
如果当前推荐目标的 qid 比客户高,但不超过 0.2,客户选择当前推荐目标的概率,会随剩余选择机会的减少而增加,大约从 0.35 升至 0.8。
如果当前推荐目标的 qid 比客户高 0.2 以上,客户选择当前推荐目标的概率,会随剩余选择机会的减少而增加,大约从 0.55 升至 1.0。
如果当前推荐目标的 qid 比客户低,但不超过 0.2,客户选择当前推荐目标的概率,会随剩余选择机会的减少而增加,大约从 0.25 升至 0.7。
如果当前推荐目标的 qid 比客户低 0.2 以上,求偶者选择当前目标的概率,会随剩余选择机会的减少而增加,大约从 0 升至 0.18。
第二种匹配方式则是基于“麦穗理论”,听起来很高大上。这里省略了关于麦穗理论的讲解,感兴趣的同学可以自行检索。具体说,就是客户在前 4 次的推荐中,不做出选择,只记下其中的最高的 qidx;从第 5 次开始,只要遇到大于或等于前 4 次最高 qidx 的推荐目标,就做出选择。
下面,我分别用两种匹配方式为 1 万名顾客选择配偶,结果会怎样呢?
# -*- encoding: utf-8 -*-
import numpy as np
class Single:
def __init__(self, qidx, times):
self.times = times # 婚介所提供的匹配次数
self.counter = 0 # 当前匹配次数
self.qidx = qidx # 客户的qidx
self.spouse = None # 匹配成功的配偶的qidx
self.histroy = list() # 基于麦穗理论的前times/e次的推荐对象的qidx
def math_classical(self, spouse):
self.counter += 1
if np.random.random() < 0.1:
self.spouse = spouse
if spouse - self.qidx >= 0.2:
if np.random.random() < 1-0.05*(10-self.counter):
self.spouse = spouse
elif spouse - self.qidx > 0:
if np.random.random() < 0.8-0.05*(10-self.counter):
self.spouse = spouse
elif self.qidx - spouse >= 0.2:
if np.random.random() < 0.18-0.02*(10-self.counter):
self.spouse = spouse
elif self.qidx - spouse >= 0:
if np.random.random() < 0.7-0.05*(10-self.counter):
self.spouse = spouse
def match_technical(self, spouse):
self.counter += 1
if self.counter < self.times/np.e:
self.histroy.append(spouse)
elif spouse >= max(self.histroy):
self.spouse = spouse
def main(math_mode, total=10000, times=10):
# 生成总数为total的客户,其qids有正态随机函数生成
singles = [Single(np.random.normal(loc=8.0, scale=0.5), times) for i in range(total)]
for p in singles:
for i in range(10):
if p.counter < 10 and not p.spouse:
spouse = np.random.normal(loc=p.qidx, scale=0.1)
getattr(p, math_mode)(spouse)
matched = np.array([(p.qidx, p.spouse) for p in singles if p.spouse])
diff = matched[:,0] - matched[:,1]
print('----------------------------------')
print('成功匹配%d人,成功率%0.2f%%'%(matched.shape[0], matched.shape[0]*100/total))
print('客户qidx均值%0.2f,配偶均值%0.2f'%(np.sum(matched[:,0])/matched.shape[0], np.sum(matched[:,1])/matched.shape[0]))
print('匹配方差%0.2f,匹配标准差%0.2f'%(diff.var(), diff.std()))
print()
if __name__ == '__main__':
print('基于传统方式择偶的统计结果')
main('math_classical')
print('基于麦穗理论择偶的统计结果')
main('match_technical')
比较两种方案的匹配成功率、匹配成功的客户的平均 qids、匹配成功的客户配偶的平均 qids、客户和配偶的 qids 的方差等,你会发现,这个结果真的有点意思。
基于传统方式择偶的统计结果
----------------------------------
成功匹配10000人,成功率100.00%
客户qidx均值8.00,配偶均值8.02
匹配方差0.01,匹配标准差0.10
基于麦穗理论择偶的统计结果
----------------------------------
成功匹配7138人,成功率71.38%
客户qidx均值8.00,配偶均值8.11
匹配方差0.00,匹配标准差0.07
结论:
基于传统方式的择偶,成功率更高(100% VS 71.38%);
基于麦穗理论择偶,配偶素质指数更高(8.11 VS 8.02);
基于麦穗理论择偶,双方qids差的标准差更小(0.07 VS 0.10),这意味着双方匹配更好。
声明:本文为 CSDN 博主「天元浪子」的原创稿件,版权归作者所有。
原文地址:https://blog.csdn.net/xufive/article/details/108214016
![]()
更多精彩推荐
鸿蒙加海思,麒麟加龙芯,组合拳能否渡劫“生态”危机
用 Python 详解《英雄联盟》游戏取胜的重要因素!
万字长文总结机器学习的模型评估与调参 | 附代码下载
“Talk is cheap, show me the code”你一行代码有多少漏洞?
科普 | 定义 Eth2.0 中的验证者质量